https://leetcode.com/problems/flip-equivalent-binary-trees/
For a binary tree T, we can define a flip operation as follows: choose any node, and swap the left and right child subtrees.
A binary tree X is flip equivalent to a binary tree Y if and only if we can make X equal to Y after some number of flip operations.
Write a function that determines whether two binary trees are flip equivalent. The trees are given by root nodes
root1 and root2.
Example 1:
Input: root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7] Output: true Explanation: We flipped at nodes with values 1, 3, and 5.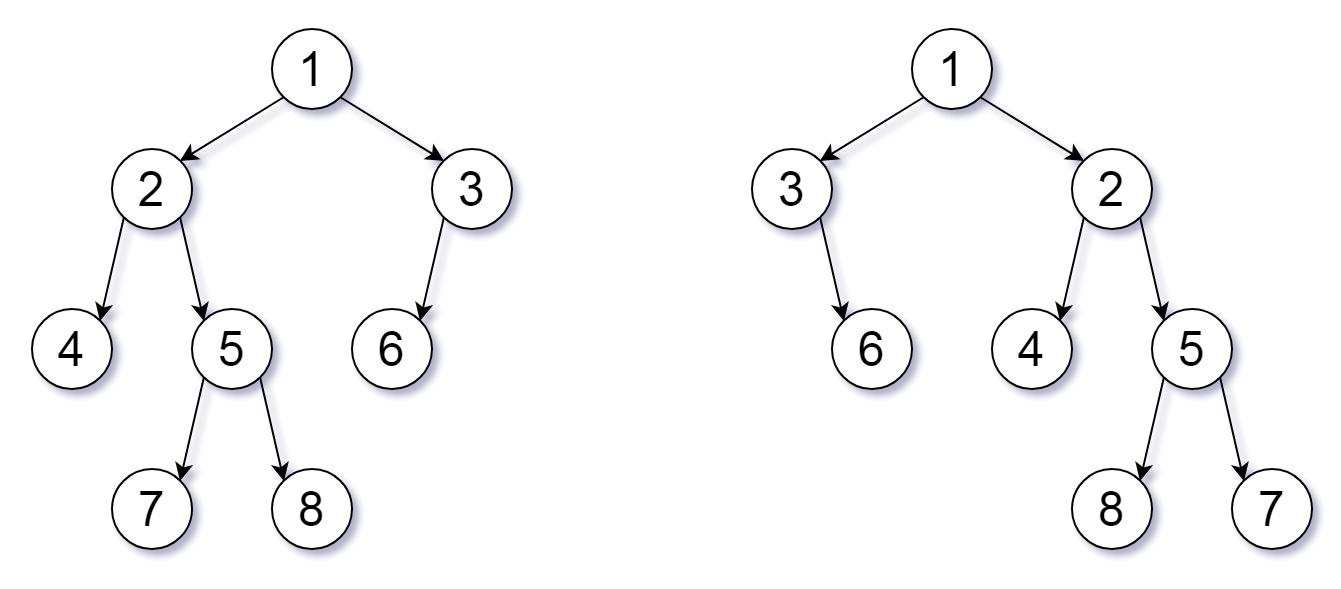
Note:
- Each tree will have at most
100nodes. - Each value in each tree will be a unique integer in the range
[0, 99].
If
root1 and root2 have the same root value, then we only need to check if their children are equal (up to ordering.)
Algorithm
There are 3 cases:
- If
root1orroot2isnull, then they are equivalent if and only if they are bothnull. - Else, if
root1androot2have different values, they aren't equivalent. - Else, let's check whether the children of
root1are equivalent to the children ofroot2. There are two different ways to pair these children.
- Time Complexity: , where are the lengths of
root1androot2. - Space Complexity: , where are the heights of the trees of
root1androot2.
public boolean flipEquiv(TreeNode root1, TreeNode root2) {
if (root1 == root2)
return true;
if (root1 == null || root2 == null || root1.val != root2.val)
return false;
return (flipEquiv(root1.left, root2.left) && flipEquiv(root1.right, root2.right)
|| flipEquiv(root1.left, root2.right) && flipEquiv(root1.right, root2.left));
}
public boolean flipEquiv(TreeNode root1, TreeNode root2) {
if (root1 == null && root2 == null)
return true;
if (root1 == null || root2 == null)
return false;
if (root1.val != root2.val)
return false;
return (flipEquiv(root1.left, root2.left) && flipEquiv(root1.right, root2.right))
|| (flipEquiv(root1.left, root2.right) && flipEquiv(root1.right, root2.left));
}
public boolean flipEquiv2(TreeNode root1, TreeNode root2) {
if (root1 == null && root2 == null)
return true;
if (root1 == null || root2 == null)
return false;
if (root1.val != root2.val)
return false;
if (hasEqualVal(root1.left, root2.left) && hasEqualVal(root1.right, root2.right)) {
return flipEquiv2(root1.left, root2.left) && flipEquiv2(root1.right, root2.right);
} else if (hasEqualVal(root1.left, root2.right) && hasEqualVal(root1.right, root2.left)) {
return flipEquiv2(root1.left, root2.right) && flipEquiv2(root1.right, root2.left);
} else {
return false;
}
}
private boolean hasEqualVal(TreeNode root1, TreeNode root2) {
if (root1 == null && root2 == null)
return true;
if (root1 == null || root2 == null)
return false;
return root1.val == root2.val;
}
Approach 2: Canonical Traversal
Intuition
Flip each node so that the left child is smaller than the right, and call this the canonical representation. All equivalent trees have exactly one canonical representation.
Algorithm
We can use a depth-first search to compare the canonical representation of each tree. If the traversals output the same values, the representations are equal.
public boolean flipEquiv(TreeNode root1, TreeNode root2) {
List<Integer> vals1 = new ArrayList();
List<Integer> vals2 = new ArrayList();
dfs(root1, vals1);
dfs(root2, vals2);
return vals1.equals(vals2);
}
public void dfs(TreeNode node, List<Integer> vals) {
if (node != null) {
vals.add(node.val);
int L = node.left != null ? node.left.val : -1;
int R = node.right != null ? node.right.val : -1;
if (L < R) {
dfs(node.left, vals);
dfs(node.right, vals);
} else {
dfs(node.right, vals);
dfs(node.left, vals);
}
}
}