LeetCode 675 - Cut Off Trees for Golf Event

https://www.cnblogs.com/grandyang/p/8379506.html

You are asked to cut off trees in a forest for a golf event. The forest is represented as a non-negative 2D map, in this map:

1. 0 represents the obstacle can't be reached.
2. 1 represents the ground can be walked through.
3. The place with number bigger than 1 represents a tree can be walked through, and this positive number represents the tree's height.

You are asked to cut off all the trees in this forest in the order of tree's height - always cut off the tree with lowest height first. And after cutting, the original place has the tree will become a grass (value 1).

You will start from the point (0, 0) and you should output the minimum steps you need to walk to cut off all the trees. If you can't cut off all the trees, output -1 in that situation.

You are guaranteed that no two trees have the same height and there is at least one tree needs to be cut off.

Example 1:

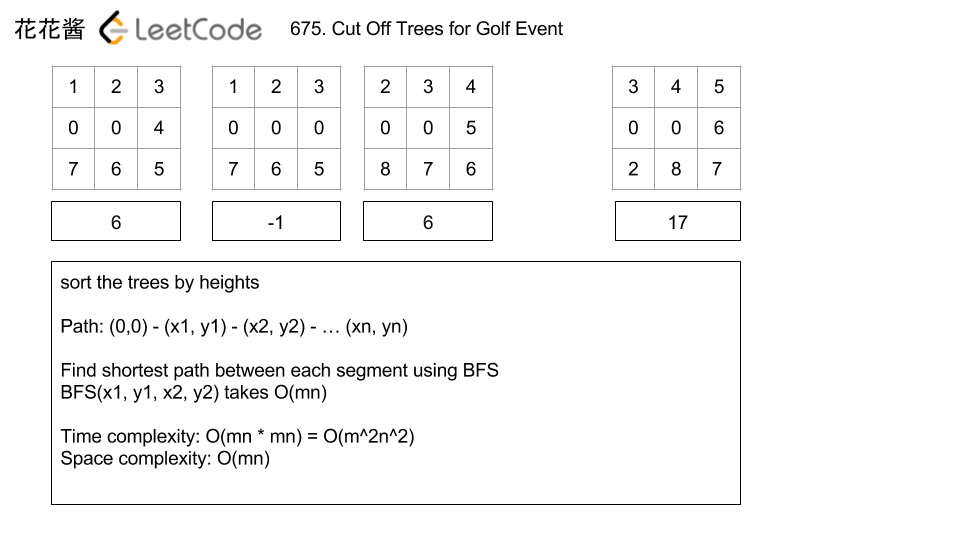
Input: 
[
 [1,2,3],
 [0,0,4],
 [7,6,5]
]
Output: 6

Example 2:

Input: 
[
 [1,2,3],
 [0,0,0],
 [7,6,5]
]
Output: -1

Example 3:

Input: 
[
 [2,3,4],
 [0,0,5],
 [8,7,6]
]
Output: 6
Explanation: You started from the point (0,0) and you can cut off the tree in (0,0) directly without walking.

Hint: size of the given matrix will not exceed 50x50.

https://leetcode.com/problems/cut-off-trees-for-golf-event/discuss/107404/Java-solution-PriorityQueue-%2B-BFS

1. Since we have to cut trees in order of their height, we first put trees (int[] {row, col, height}) into a priority queue and sort by height.
2. Poll each tree from the queue and use BFS to find out steps needed.

The worst case time complexity could be O(m^2 * n^2) (m = number of rows, n = number of columns) since there are m * n trees and for each BFS worst case time complexity is O(m * n) too.

class Solution {
    static int[][] dir = {{0,1}, {0, -1}, {1, 0}, {-1, 0}};

    public int cutOffTree(List<List<Integer>> forest) {
        if (forest == null || forest.size() == 0) return 0;
        int m = forest.size(), n = forest.get(0).size();

        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[2] - b[2]);

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (forest.get(i).get(j) > 1) {
                    pq.add(new int[] {i, j, forest.get(i).get(j)});
                }
            }
        }

        int[] start = new int[2];
        int sum = 0;
        while (!pq.isEmpty()) {
            int[] tree = pq.poll();
            int step = minStep(forest, start, tree, m, n);

            if (step < 0) return -1;
            sum += step;

            start[0] = tree[0];
            start[1] = tree[1];
        }

        return sum;
    }

    private int minStep(List<List<Integer>> forest, int[] start, int[] tree, int m, int n) {
        int step = 0;
        boolean[][] visited = new boolean[m][n];
        Queue<int[]> queue = new LinkedList<>();
        queue.add(start);
        visited[start[0]][start[1]] = true;

        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                int[] curr = queue.poll();
                if (curr[0] == tree[0] && curr[1] == tree[1]) return step;

                for (int[] d : dir) {
                    int nr = curr[0] + d[0];
                    int nc = curr[1] + d[1];
                    if (nr < 0 || nr >= m || nc < 0 || nc >= n 
                        || forest.get(nr).get(nc) == 0 || visited[nr][nc]) continue;
                    queue.add(new int[] {nr, nc});
                    visited[nr][nc] = true;
                }
            }
            step++;
        }

        return -1;
    }

http://www.programmersought.com/article/222929242/

Give an int two-dimensional array representing the height of the tree at position i j , 0 is unreachable, 1 is flat. Cut the trees in order from short to high. Ask to take at least a few steps to finish.

Using a priority queue to find which tree we would cut. Using BFS to find the shortest steps. Using int[] store the postion and height of a tree. Add all of them into pq with ascending sorting.

Then preform BFS to find the steps needed to get the next position.

这道题让我们砍掉所有高度大于1的树，而且要求是按顺序从低到高来砍，那么本质实际上还是要求任意两点之间的最短距离啊。对于这种类似迷宫遍历求最短路径的题，BFS是不二之选啊。那么这道题就对高度相邻的两棵树之间调用一个BFS，所以我们可以把BFS的内容放倒子函数helper中来使用。那么我们首先就要将所有的树从低到高进行排序，我们遍历原二位矩阵，将每棵树的高度及其横纵坐标取出来，组成一个三元组，然后放到vector中，之后用sort对数组进行排序，因为sort默认是以第一个数字排序，这也是为啥我们要把高度放在第一个位置。然后我们就遍历我们的trees数组，我们的起始位置是（0，0），终点位置是从trees数组中取出的树的位置，然后调用BFS的helper函数，这个BFS的子函数就是很基本的写法，没啥过多需要讲解的地方，会返回最短路径的值，如果无法到达目标点，就返回-1。所以我们先检查，如果helper函数返回-1了，那么我们就直接返回-1，否则就将cnt加到结果res中。然后更新我们的起始点为当前树的位置，然后循环取下一棵树即可

https://www.acwing.com/solution/LeetCode/content/534/

你被请来给一个要举办高尔夫比赛的树林砍树。树林由一个非负的二维数组表示，在这个数组中：

• 0 表示 障碍，无法触碰到。
• 1 表示可以行走的 地面。
• 比 1 大的数 表示一颗允许走过的 树 的，这个整数表示数的高度。

你被要求按照树的高度从低向高砍掉所有的树，每砍过一颗树，树的高度变为 1。

你将从（0，0）点开始工作，你应该返回你砍完所有树需要走的最小步数。如果你无法砍完所有的树，返回 -1 。

可以保证的是，没有两棵 树 的高度是相同的，并且至少有一颗树需要被砍。

1. 首先将所有的树和坐标放到一个数组中，并且按照高度从小到大排序。
2. 接着遍历每一棵树，并通过BFS计算出从上一棵树走到这一棵树需要的最少步数；若无法达到，则答案就是 -1。

https://leetcode.com/articles/cutoff-trees-for-golf-event/
http://reeestart.me/2018/04/22/LeetCode-675-Cut-Off-Trees-for-Golf-Event/

X, Videos
花花酱 LeetCode 675. Cut Off Trees for Golf Event - 刷题找工作 EP55

LeetCode 882 - Reachable Nodes In Subdivided Graph

https://leetcode.com/articles/reachable-nodes-in-subdivided-graph/

Starting with an undirected graph (the "original graph") with nodes from 0 to N-1, subdivisions are made to some of the edges.

The graph is given as follows: edges[k] is a list of integer pairs (i, j, n) such that (i, j) is an edge of the original graph,

and n is the total number of new nodes on that edge. 

Then, the edge (i, j) is deleted from the original graph, n new nodes (x_1, x_2, ..., x_n) are added to the original graph,

and n+1 new edges (i, x_1), (x_1, x_2), (x_2, x_3), ..., (x_{n-1}, x_n), (x_n, j) are added to the original graph.

Now, you start at node 0 from the original graph, and in each move, you travel along one edge. 

Return how many nodes you can reach in at most M moves.

Example 1:

Input: edges = [[0,1,10],[0,2,1],[1,2,2]], M = 6, N = 3
Output: 13
Explanation: 
The nodes that are reachable in the final graph after M = 6 moves are indicated below.

Example 2:

Input: edges = [[0,1,4],[1,2,6],[0,2,8],[1,3,1]], M = 10, N = 4
Output: 23

Note:

1. 0 <= edges.length <= 10000
2. 0 <= edges[i][0] < edges[i][1] < N
3. There does not exist any i != j for which edges[i][0] == edges[j][0] and edges[i][1] == edges[j][1].
4. The original graph has no parallel edges.
5. 0 <= edges[i][2] <= 10000
6. 0 <= M <= 10^9
7. 1 <= N <= 3000
8. A reachable node is a node that can be travelled to using at most M moves starting from node 0.

X. Dijkstra's

https://zxi.mytechroad.com/blog/graph/leetcode-882-reachable-nodes-in-subdivided-graph/

Compute the shortest from 0 to rest of the nodes. Use HP to mark the maximum moves left to reach each node.

HP[u] = a, HP[v] = b, new_nodes[u][v] = c

nodes covered between a<->b = min(c, a + b)

Time complexity: O(ElogE)

Space complexity: O(E)

Treating the original graph as a weighted, undirected graph, we can use Dijkstra's algorithm to find all reachable nodes in the original graph. However, this won't be enough to solve examples where subdivided edges are only used partially.

When we travel along an edge (in either direction), we can keep track of how much we use it. At the end, we want to know every node we reached in the original graph, plus the sum of the utilization of each edge.

Algorithm

We use Dijkstra's algorithm to find the shortest distance from our source to all targets. This is a textbook algorithm, refer to this link for more details.

Additionally, for each (directed) edge (node, nei), we'll keep track of how many "new" nodes (new from subdivision of the original edge) were used. At the end, we'll sum up the utilization of each edge.

  public int reachableNodes(int[][] edges, int M, int N) {
      Map<Integer, Map<Integer, Integer>> graph = new HashMap();
      for (int[] edge: edges) {
          int u = edge[0], v = edge[1], w = edge[2];
          graph.computeIfAbsent(u, x->new HashMap()).put(v, w);
          graph.computeIfAbsent(v, x->new HashMap()).put(u, w);
      }

      PriorityQueue<ANode> pq = new PriorityQueue<ANode>(
          (a, b) -> Integer.compare(a.dist, b.dist));
      pq.offer(new ANode(0, 0));

      Map<Integer, Integer> dist = new HashMap();
      dist.put(0, 0);
      Map<Integer, Integer> used = new HashMap();
      int ans = 0;

      while (!pq.isEmpty()) {
          ANode anode = pq.poll();
          int node = anode.node;
          int d = anode.dist;

          if (d > dist.getOrDefault(node, 0)) continue;
          // Each node is only visited once.  We've reached
          // a node in our original graph.
          ans++;

          if (!graph.containsKey(node)) continue;
          for (int nei: graph.get(node).keySet()) {
              // M - d is how much further we can walk from this node;
              // weight is how many new nodes there are on this edge.
              // v is the maximum utilization of this edge.
              int weight = graph.get(node).get(nei);
              int v = Math.min(weight, M - d);
              used.put(N * node + nei, v);

              // d2 is the total distance to reach 'nei' (neighbor) node
              // in the original graph.
              int d2 = d + weight + 1;
              if (d2 < dist.getOrDefault(nei, M+1)) {
                  pq.offer(new ANode(nei, d2));
                  dist.put(nei, d2);
              }
          }
      }

      // At the end, each edge (u, v, w) can be used with a maximum
      // of w new nodes: a max of used[u, v] nodes from one side,
      // and used[v, u] nodes from the other.
      // [We use the encoding (u, v) = u * N + v.]
      for (int[] edge: edges) {
          ans += Math.min(edge[2], used.getOrDefault(edge[0] * N + edge[1], 0) +
                                   used.getOrDefault(edge[1] * N + edge[0], 0) );
      }

      return ans;
  }
class ANode {
  int node, dist;
  ANode(int n, int d) {
      node = n;
      dist = d;
  }
}

https://leetcode.com/problems/reachable-nodes-in-subdivided-graph/discuss/156777/Java-Dijkstra-Solution
This seems like a standard Dijkstra problem. Remember to calculate move even cannot reach the next node.

    public int reachableNodes(int[][] edges, int M, int N) {
        int[][] graph = new int[N][N];
        for (int i = 0; i < N; i++) {
            Arrays.fill(graph[i], -1);
        }
        for (int[] edge : edges) {
            graph[edge[0]][edge[1]] = edge[2];
            graph[edge[1]][edge[0]] = edge[2];
        }
        int result = 0;
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> (b[1] - a[1]));
        boolean[] visited = new boolean[N];
        pq.offer(new int[]{0, M});
        while (!pq.isEmpty()) {
            int[] cur = pq.poll();
            int start = cur[0];
            int move = cur[1];
            if (visited[start]) {
                continue;
            }
            visited[start] = true;
            result++;
            for (int i = 0; i < N; i++) {
                if (graph[start][i] > -1) {
                    if (move > graph[start][i] && !visited[i]) {
                        pq.offer(new int[]{i, move - graph[start][i] - 1});
                    }
                    graph[i][start] -= Math.min(move, graph[start][i]);
                    result += Math.min(move, graph[start][i]);
                }
            }
        }
        return result;
    }

https://leetcode.com/problems/reachable-nodes-in-subdivided-graph/discuss/156739/C%2B%2BJavaPython-Dijkstra-%2B-Priority-Queue

Store edges to another 2D hashtable e, so that we can easier get length between two node by e[i][j].
seen[i] means that we can arrive at node i and have seen[i] moves left.

We use a dijkstra algorithm in this solution.
Priority queue pq store states (moves left, node index).
So every time when we pop from pq, we get the state with the most moves left.

In the end, we calculate the number of nodes that we can reach.

res = seen.length
For every edge e[i][j]:
res += min(seen.getOrDefault(i, 0) + seen.getOrDefault(j, 0), e[i][j])

Time Complexity:
Reminded by @kAc:
Dijkstra + Heap is O(E log E)
Dijkstra + Fibonacci heap is O(N log N + E)

    public int reachableNodes(int[][] edges, int M, int N) {
        HashMap<Integer, HashMap<Integer, Integer>> e = new HashMap<>();
        for (int i = 0; i < N; ++i) e.put(i, new HashMap<>());
        for (int[] v : edges) {
            e.get(v[0]).put(v[1], v[2]);
            e.get(v[1]).put(v[0], v[2]);
        }
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> (b[0] - a[0]));
        pq.offer(new int[] {M, 0});
        HashMap<Integer, Integer> seen = new HashMap<>();
        while (!pq.isEmpty()) {
            int moves = pq.peek()[0], i = pq.peek()[1];
            pq.poll();
            if (!seen.containsKey(i)) {
                seen.put(i,moves);
                for (int j : e.get(i).keySet()) {
                    int moves2 = moves - e.get(i).get(j) - 1;
                    if (!seen.containsKey(j) && moves2 >= 0)
                        pq.offer(new int[] { moves2, j});
                }
            }
        }
        int res = seen.size();
        for (int[] v : edges) {
            int a = seen.getOrDefault(v[0],0);
            int b = seen.getOrDefault(v[1],0);
            res += Math.min(a + b, v[2]);
        }
        return res;
    }

https://leetcode.com/problems/reachable-nodes-in-subdivided-graph/discuss/157252/Logical-Thinking-with-Clear-Code

Logical Thinking
The problem is to get maximum number of nodes I can reach from node 0 within M moves. If I figure out each node's shortest distance to src, the one with distance <= M moves should be reachable. In this way, the problem can be regarded as a single-source shortest-path problem, which can be solved by Dijkstra's Algorithm.

Instead of maintaining a MinHeap which keeps track of shortest distances to the source, we maintain a MaxHeap that keeps track of maximum moves remained for each node. Since for a node,

moves remained + distance from current node to source = M

The bigger moves remained is, the smaller the distance will be. Thus, the MaxHeap can also promise the shortest distance.

We rebuild the graph to a weighted graph such that weight of an edge is total number of new nodes on that edge.

    public int reachableNodes(int[][] edges, int M, int N) {
        int[][] graph = new int[N][N];

        for (int[] tmp : graph) {
            Arrays.fill(tmp, -1);
        }
        for (int[] edge: edges) { // e.g. graph[0][1] = 4
            graph[edge[0]][edge[1]] = edge[2];
            graph[edge[1]][edge[0]] = edge[2];
        }
        int result = 0;
        
        boolean[] visited = new boolean[N];
        PriorityQueue<int[]> pq_node_movesRemained = new PriorityQueue<>((a, b) -> (b[1] - a[1]));
        pq_node_movesRemained.add(new int[] {0, M});
        
        while (!pq_node_movesRemained.isEmpty()) {
            int[] tmp = pq_node_movesRemained.poll();
            int node = tmp[0];
            int movesRemained = tmp[1];
            if (visited[node]) { 
                continue;
            }
            visited[node] = true;
            result++;
            for (int nei = 0; nei < N; nei++) {
                if (graph[node][nei] != -1) {
                    if (!visited[nei] && movesRemained >= graph[node][nei] + 1) {
                        pq_node_movesRemained.add(new int[]{nei, movesRemained - graph[node][nei] - 1});
                    }
                    int movesCost = Math.min(movesRemained, graph[node][nei]);
                    graph[nei][node] -= movesCost;
                    result += movesCost;
                }
            }
        }
        
        return result;
    }

http://hehejun.blogspot.com/2018/08/leetcodereachable-nodes-in-subdivided.html
我们直接把输入看成带权图即可，这道题本质上就是最短路径，但是区别是，如果我们发现M步之内无法从当前点去往下一个点，我们仍然会取当前边的一部分。比如从u到v需要10步，我们只剩下6不可以走，我们仍然会取这六个点。这里有一个情况需要注意一下，就是同一条边，如果我们只能取部分，可能会取到两次。比如u到v存在一条无向边，长度为10，我们到u的时候还剩8步，我们取了8个点。然后我们从其他某个点到达v，还剩5步，如果我们取了5个点这里就有重复了，长度为10的边我们却取了13个点，这是明显不行的。这里我们需要做一些特殊的处理，假设我们现在在顶点u，剩下的步数不够到达顶点v，连接u和v的边的长度为w，我们还剩下k步：

• 如果v是还没有visited过的点，我们取边上k个点即可。得到source到v的最短路径shortestPath[v]
• 如果v是已经被visited过的点，有可能出现上面提到的重复的情况。我们需要查看visit v的时候已经取了多少个节点，这个我们可以通过shortestPath[v]推出，等于总步数M - shortestPath[v]。根据这个值来决定取k还是w - (M - shortestPath[v])即可。

时间复杂度就是Dijkstra的复杂度O(E * log V)，空间复杂度O(V + E)，代码如下：

(最短路) $O((n+m)\log m)$

1. 将添加的结点数 + 1 作为原图边的路径长度，然后以 0 号点为起点，求单源最短路。
2. 假设求得的最短路数组为 dis。统计 dis[x] <= M 的结点 x，这些都可以作为可到达结点。
3. 然后枚举每一条边，如果边的两个端点都可到达，则答案加上 min(edge[i][2], 2 * M - dis[x] - dis[y])；如果只有结点 x 可以到达，则答案加上 min(edge[i][2], M - dis[x])；结点 y 可以到达同理。

时间复杂度

• 采用 dijkstra 算法，求最短路的时间复杂度为 $O((n+m)\log m)$，其中 n 为点数，m 为边数。然后需要遍历每个点和每条边，故总时间复杂度为 $O((n+m)\log m)$。

空间复杂度

• 需要额外的数组来存图，以及记录最短距离，采用 dijkstra 算法需要额外的堆空间，故总空间复杂度为 $O(n+m)$。

https://www.acwing.com/solution/LeetCode/content/770/

从具有 0 到 N-1 的结点的无向图（“原始图”）开始，对一些边进行细分。

该图给出如下：edges[k] 是整数对 (i, j, n) 组成的列表，使 (i, j) 是原始图的边。

n 是该边上新结点的总数

然后，将边 (i, j) 从原始图中删除，将 n 个新结点 (x_1, x_2, ..., x_n) 添加到原始图中，

将 n+1 条新边 (i, x_1), (x_1, x_2), (x_2, x_3), ..., (x_{n-1}, x_n), (x_n, j) 添加到原始图中。

现在，你将从原始图中的结点 0 处出发，并且每次移动，你都将沿着一条边行进。

返回最多 M 次移动可以达到的结点数。

X. Video
花花酱 LeetCode 882. Reachable Nodes In Subdivided Graph - 刷题找工作 EP215