整数划分问题

http://www.cnblogs.com/xiaoxian1369/archive/2011/09/12/2174212.html

整数划分 －－－ 一个老生长谈的问题:　　1) 练练组合数学能力.
　　2) 练练递归思想
　　3) 练练DP
　　总之是一道经典的不能再经典的题目:
　　这道好题求:
　　1. 将n划分成若干正整数之和的划分数。
　　2. 将n划分成k个正整数之和的划分数。
　　3. 将n划分成最大数不超过k的划分数。
　　4. 将n划分成若干奇正整数之和的划分数。
　　5. 将n划分成若干不同整数之和的划分数。

1.将n划分成不大于m的划分法： 

 　　1).若是划分多个整数可以存在相同的：

 　　 dp[n][m]= dp[n][m-1]+ dp[n-m][m]  dp[n][m]表示整数 n 的划分中，每个数不大于 m 的划分数。
     　　则划分数可以分为两种情况:
     　　a.划分中每个数都小于 m，相当于每个数不大于 m- 1, 故划分数为 dp[n][m-1].
    　　 b.划分中有一个数为 m. 那就在 n中减去 m ,剩下的就相当于把 n-m 进行划分， 故划分数为 dp[n-m][m];

　　2).若是划分多个不同的整数：

　　dp[n][m]= dp[n][m-1]+ dp[n-m][m-1]   dp[n][m]表示整数 n 的划分中，每个数不大于 m 的划分数。
   　　 同样划分情况分为两种情况：
    　　a.划分中每个数都小于m,相当于每个数不大于 m-1,划分数为 dp[n][m-1].
    　　b.划分中有一个数为 m.在n中减去m,剩下相当对n-m进行划分，

　　　并且每一个数不大于m-1，故划分数为 dp[n-m][m-1]

　　2.将n划分成k个数的划分法：

　　　　dp[n][k]= dp[n-k][k]+ dp[n-1][k-1];

   　　方法可以分为两类：
   　　　　第一类: n 份中不包含 1 的分法，为保证每份都 >= 2，可以先拿出 k 个 1 分
   　　到每一份，然后再把剩下的 n- k 分成 k 份即可，分法有: dp[n-k][k]
  　　 　　第二类: n 份中至少有一份为 1 的分法，可以先那出一个 1 作为单独的1份，剩
   　　下的 n- 1 再分成 k- 1 份即可，分法有：dp[n-1][k-1]

　　

　　3.将n划分成若干奇数的划分法：（不懂）

　　　　g[i][j]:将i划分为j个偶数

　　　　f[i][j]:将i划分为j个奇数
　　   g[i][j] = f[i - j][j];
   　　f[i][j] = f[i - 1][j - 1] + g[i - j][j];

int num[nmax][nmax]; //将i划分为不大于j的个数
int num1[nmax][nmax]; //将i划分为不大于j的不同的数
int num2[nmax][nmax]; //将i划分为j个数
int f[nmax][nmax]; //将i划分为j个奇数
int g[nmax][nmax]; //将i划分为j个偶数
void init() {
    int i, j;
    for (i = 0; i < nmax; i++) {
        num[i][0] = 0, num[0][i] = 0, num1[i][0] = 0, num1[0][i] = 0, num2[i][0] =
                0, num2[0][i] = 0;
    }
    for (i = 1; i < nmax; i++) {
        for (j = 1; j < nmax; j++) {
            if (i < j) {
                num[i][j] = num[i][i];
                num1[i][j] = num1[i][i];
                num2[i][j] = 0;
            } else if (i == j) {
                num[i][j] = num[i][j - 1] + 1;
                num1[i][j] = num1[i][j - 1] + 1;
                num2[i][j] = 1;

            } else {
                num[i][j] = num[i][j - 1] + num[i - j][j];
                num1[i][j] = num1[i][j - 1] + num1[i - j][j - 1];
                num2[i][j] = num2[i - 1][j - 1] + num2[i - j][j];
            }
        }
    }
    f[0][0] = 1, g[0][0] = 1;
    for (i = 1; i < nmax; i++) {
        for (j = 1; j <= i; j++) {
            g[i][j] = f[i - j][j];
            f[i][j] = f[i - 1][j - 1] + g[i - j][j];
        }
    }

将正整数划分成连续的正整数之和如15可以划分成4种连续整数相加的形式：
15
7 8
4 5 6
1 2 3 4 5

    首先考虑一般的形式，设n为被划分的正整数，x为划分后最小的整数，如果n有一种划分，那么
结果就是x,如果有两种划分，就是x和x x + 1， 如果有m种划分，就是 x 、x x + 1 、 x x + 1 x + 2 、... 、x x + 1 x + 2 ... x + m - 1
将每一个结果相加得到一个公式(i * x + i * (i - 1) / 2) = n，i为当前划分后相加的正整数个数。
满足条件的划分就是使x为正整数的所有情况。
如上例，当i = 1时，即划分成一个正整数时，x = 15， 当i = 2时， x = 7。
当x = 3时，x = 4， 当x = 4时，4/9，不是正整数，因此，15不可能划分成4个正整数相加。
当x = 5时，x = 1。

    这里还有一个问题，这个i的最大值是多少？不过有一点可以肯定，它一定比n小。我们可以做一个假设，
假设n可以拆成最小值为1的划分，如上例中的1 2 3 4 5。这是n的最大数目的划分。如果不满足这个假设，
那么 i 一定比这个划分中的正整数个数小。因此可以得到这样一个公式i * (i + 1) / 2 <= n，即当i满足
这个公式时n才可能被划分。

void split(int n) {
    int i, j, te, x, xlen;
    for (i = 1, xlen = 0; (te = i * (i - 1) / 2) < n; i++) {
        x = n - te;
        if (x % i == 0) {
            x /= i;
            printf("%d", x);
            for (j = 1; j < i; j++) {
                printf("%d ", x + j);
            }
            printf("\n");
            xlen++;
        }
    }
    printf("%d\n", xlen);
}

　　求划分因子乘积最大的一个划分及此乘积
　　问题简述：给定一个正整数n, 则在n所有的划分中, 求因子乘积最大的一个划分及此乘积。例如：8 = {8}, {7, 1}, {6, 2}, {5, 3}, {4, 4}, {3, 3, 2}, {2, 2, 2, 2} 等，那么在这些当中，3 * 3 * 2 的乘积最大，所以输出整个划分
和这个乘积 18。
　　算法分析：这是我在某个论坛上看到的问题，以及别人针对此问题的数学分析，现简单的整理如下：
　　(1)对于任意大于等于4的正整数m, 存在一个划分m = m1+m2, 使 m1*m2 >= m证: 令m1 = int(m/2), 则 m1 >= 2 ， m2 = m-m1; 那么m2 > 2，并且 m2 >= m/2 >= m1;    m1*m2 >= 2*m2 >= m; 证毕;
该证明简单的来说就是：对于一个大于等于4的正整数m，存在一个2块划分的因子，这两个因子的乘积总是不小于原数m本身。
　　(2)由(1)知此数最终可以分解为 2^r * 3^s。现证明 r <= 2;
　　证：若r > 2, 则至少有3个因子为2, 而2*2*2 < 3*3;
　　所以可以将3个为2的因子,换为两个因子3；积更大；证毕。
　　综合(1)，(2)，则有：任何大于4的因子都可以有更好的分解, 而4可以分解为2*2。
　　所以：此数应该分解为 2^k1 * 3^k2。而且可以证明 k1>=0 并且 k1 <= 2，因此：
　　   A.当n = 3*r 时, 分解为 3^r
 　　  B.当n = 3*r+1时, 分解为 3^(r-1)*2*2
   　　C.当n = 3*r+2时, 分解为 3^r*2
　　剩下编程处理，那就是太简单了，首先是处理 <= 4的特殊情况，再对>4的情况进行模3的3种情况的判断，最后一一输出。可见，数学在整数划分问题上有太强的功能。谁叫这个问题叫整数划分呢，不与数学密切才怪! ^_^。

　　小学六年级奥数---整数划分(有用结论)

　　例1：把14分拆成若干个自然数的和，再求出这些数的积，要使得到的积最大，应该把14如何分拆？这个最大的乘积是多少？

　　分析与解：我们先考虑分成哪些数时乘积才能尽可能地大。
　　首先，分成的数中不能有1，这是显然的。
　　其次，分成的数中不能有大于4的数，否则可以将这个数再分拆成2与另外一个数的和，这两个数的乘积一定比原数大，例如7就比它分拆成的2和5的乘积小。
　　再次，因为4=2×2，故我们可以只考虑将数分拆成2和3。
　　注意到2+2+2=6，2×2×2=8；3+3=6，3×3=9，因此分成的数中若有三个2，则不如换成两个3，换句话说，分成的数中至多只能有两个2，其余都是3。根据上面的讨论，我们应该把14分拆成四个3与一个2之和，即14=3+3+3+3+2，这五数的积有最大值 3×3×3×3×2=162。
　　将上述结论推广为一般情形便是：
　　把自然数S（S＞1）分拆为若干个自然数的和：   S=a1+a2+…+an，则当a1，a2，…，an中至多有两个2，其余都是3时，其连乘积m=a1a2…an有最大值。

　　例2：把1993分拆成若干个互不相等的自然数的和，且使这些自然数的乘积最大，该乘积是多少？
解：由于把1993分拆成若干个互不相等的自然数的和的分法只有有限种，因而一定存在一种分法，使得这些自然数的乘积最大。
　　若1作因数，则显然乘积不会最大。把1993分拆成若干个互不相等的自然数的和，因数个数越多，乘积越大。为了使因数个数尽可能地多，我们把1993分成2+3…+n直到和大于等于1993。
若和比1993大1，则因数个数至少减少1个，为了使乘积最大，应去掉最小的2，并将最后一个数（最大）加上1。
若和比1993大k（k≠1），则去掉等于k的那个数，便可使乘积最大。
所以n=63。因为2015-1993=22，所以应去掉22，把1993分成（2+3+…+21）+（23+24+…+63）

这一形式时，这些数的乘积最大，其积为  2×3×…×21×23×24×…×63。

https://www.jianshu.com/p/14211b33fbc4

【问题】将整数n表示为一系列正整数的和。
n = n1 + n2 + ...+ nk (n1 >= n2>=......>=nk>=1,k>=1)
并称之为n的划分。不同的划分个数称为正整数n的划分数，p(n)
建立如下递归关系：
在不同的划分中，将最大的加数n1不大于m的划分数计做q(n,m)
1.q(n,1) = 1,n >= 1;表示，最大加数小于等于1，就是，n1<=1.而n1>=1,因此n1 = 1，该种类型划分只有一种。
2,q(n,m) = q(n,n),m>=n;因此，m >=n > n1. 对于数字m和n他们划分的最大加数，都不会比n大，就说明划分数相同。
3.q(n,n) = 1 + q(n,n-1);n的划分由n1 = n,和n1 <= n-1构成。
4.q(n,m) = q(n,m-1) + q(n-m,m),n > m > 1;
n的最大划分数n1不大于m的划分数（n1 <= m）由，n1 = m和n1 <= m-1构成。
n1 = m,则n2 + n3 + ...+nk = n - m,在对n-m中找到最大为m的划分。表示为q(n-m,m);
n1 <= m - 1,表为q(n,m-1)

https://www.cnblogs.com/radiumlrb/p/5797168.html

http://www.voidcn.com/article/p-mmrkvgjh-bcg.html

但我在做51nod的时候发现数据给的范围很大(5*10^4)，这种方法不仅内存存不下，而且还TLE

下面给出n个数拆成不同数的方案的O(nsqrt(n))算法

dp[i][j]代表i个数相加等于j
由于有不同的数最多不超过O(sqrt(n))算法个，则可以优化

dp[i][j] = dp[i-1][j-i] + dp[i][j-i]

这个递推方程的转移含义是i-1个数每个数都加1,最后再添上一个1，就从dp[i-1][j-i]转到dp[i][j],还有就是i个数每个数都加1，就从dp[i][j-i]转到dp[i][j]

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <string>
#include <cmath>

int dp[600][51000];
int const mod = 1e9+7;
using namespace std;
int main()
{

  int n;
  while(scanf("%d",&n) != EOF){
     dp[0][0] = 1;
      for(int i =1; i <= 2*(int)sqrt(n); i++ )
      {
          for(int j = 0; j <= n; j++)
          {
              dp[i][j] = (dp[i-1][j-i] + dp[i][j-i])%mod;
          }
      }

      int ans = 0;
      for(int i =1; i <= 2*(int)sqrt(n); i++ )
      {
          ans += dp[i][n];
          ans %= mod;
      }
          printf("%d\n",ans);
  }

  return 0;
}

那么当将n划分成若干正整数之和的划分数呢？
可以相同，那么上面那个方法就不行了
可以用5边形数来求
参考资料
https://en.wikipedia.org/wiki/Partition_(number_theory)

用一个公式就行

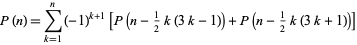
其中n-k*(3*k-1)/2>=0,n-k*(3*k+1)/2>=0；
注意两个条件要分开判断，有大于0的就加上相应的f，不是两个同时成立或者不成立

这个公式的时间复杂度是O(n^1.5)

#include <iostream>
#include <cstring>
#include <cmath>
using namespace std;

long long tar[100002];
const int MOD=1000000007;

void init()
{
    memset(tar,0,sizeof(tar));
    tar[0]=1;

    for(int i=1;i<=50000;i++)
    {
        int nbit;
        for(int j=1;;j++)
        {
            int element1,element2;
            element1=i-j*(3*j-1)/2;
            element2=i-j*(3*j+1)/2;
            if(j&1)
                nbit=1;
            else if(j%2==0)
                nbit=-1;

            if(element2<0 && element1<0)
                break;

            if(element1>=0)
            {
                tar[i]=(tar[i]+nbit*tar[element1])%MOD;
            }
            if(element2>=0)
            {
                tar[i]=(tar[i]+nbit*tar[element2])%MOD;
            }
        }
        tar[i]=(tar[i]+MOD)%MOD;
    }


}

int main()
{

    init();
    int rat;
    while(cin>>rat)
    {

        cout<<tar[rat]<<endl;
    }
    return 0;
}

LeetCode 740 - Delete and Earn

https://leetcode.com/problems/delete-and-earn/description/

Given an array nums of integers, you can perform operations on the array.

In each operation, you pick any nums[i] and delete it to earn nums[i] points. After, you must delete every element equal to nums[i] - 1 or nums[i] + 1.

You start with 0 points. Return the maximum number of points you can earn by applying such operations.

Example 1:

Input: nums = [3, 4, 2]
Output: 6
Explanation: 
Delete 4 to earn 4 points, consequently 3 is also deleted.
Then, delete 2 to earn 2 points. 6 total points are earned.

Example 2:

Input: nums = [2, 2, 3, 3, 3, 4]
Output: 9
Explanation: 
Delete 3 to earn 3 points, deleting both 2's and the 4.
Then, delete 3 again to earn 3 points, and 3 again to earn 3 points.
9 total points are earned.

Note:

The length of nums is at most 20000.

Each element nums[i] is an integer in the range [1, 10000].

    int deleteAndEarn(vector<int>& nums) {

        if (nums.empty()) return 0;

        const auto range = minmax_element(nums.begin(), nums.end());

        const int l = *(range.first);

        const int r = *(range.second);        

        vector<int> points(r - l + 1, 0);

        for (const int num : nums)

            points[num - l] += num;

        return rob(points);

    }

private:

    // From LeetCode 198. House Robber

    int rob(const vector<int>& nums) {

        int dp2 = 0;

        int dp1 = 0;

        for (int i = 0; i < nums.size() ; ++i) {

            int dp = max(dp2 + nums[i], dp1);

            dp2 = dp1;

            dp1 = dp;

        }

        return dp1;

    }

http://buttercola.blogspot.com/2018/10/leetcode-740-delete-and-earn.html

There are several tricks in the problem.
 -- Since each element nums[i] is within the range of [1, 10000], we can use the bucket sort to sort the nums.
 -- For deleting each nums[i], we can delete all same numbers together. So when we do the bucket sort, we can sum up all the repeated numbers in the same bucket. 
 -- Then the problem is a classic backpack problem. 

Define take[10001] and skip[10001], where take[i] means for number i, we delete the number i, the max number of points. skip[i] means we don't delete it.

Then the transit function should be:
take[i] = skip[i - 1] +  values[i]
skip[i] = Math.max(take[i - 1], skip[i - 1]);

http://www.cnblogs.com/grandyang/p/8176933.html

好了，来做题吧。这道题给了我们一个数组，每次让我们删除一个数字，删除的数字本身变为了积分累积，并且要同时移除之前数的加1和减1的数，但此时移除的数字不累计积分，让我们求最多能获得多少积分。博主最开始尝试的方法是积分大小来排列，先删除大的数字，但是不对。于是乎，博主发现相同的数字可以同时删除，于是就是建立了每个数字和其出现次数之间的映射，然后放到优先队列里，重写排序方式comparator为数字乘以其出现次数，先移除能产生最大积分的数字，可是还是不对。其实这道题跟之前那道House Robber的本质是一样的，那道题小偷不能偷相邻的房子，这道题相邻的数字不能累加积分，是不是一个道理？那么对于每一个数字，我们都有两个选择，拿或者不拿。如果我们拿了当前的数字，我们就不能拿之前的数字（如果我们从小往大遍历就不需要考虑后面的数字），那么当前的积分就是不拿前面的数字的积分加上当前数字之和。如果我们不拿当前的数字，那么对于前面的数字我们既可以拿也可以不拿，于是当前的积分就是拿前面的数字的积分和不拿前面数字的积分中的较大值。这里我们用take和skip分别表示拿与不拿上一个数字，takei和skipi分别表示拿与不拿当前数字，每次更新完当前的takei和skipi时，也要更新take和skip，为下一个数字做准备，最后只要返回take和skip中的较大值即可

https://zxi.mytechroad.com/blog/dynamic-programming/leetcode-740-delete-and-earn/
Because all numbers are positive, if we "take" a number (use it to score points), we might as well take all copies of it, since we've already erased all its neighbors. We could keep a count of each number so we know how many points taking a number is worth total.

Now let's investigate what happens when we add a new number X (plus copies) that is larger than all previous numbers. Naively, our answer would be the previous answer, plus the value of X - which can be solved with dynamic programming. However, this fails if our previous answer had a number taken that was adjacent to X.

Luckily, we can remedy this. Let's say we knew using, the value of our previous answer, and avoid, the value of our previous answer that doesn't use the previously largest value prev. Then we could compute new values of using and avoid appropriately.

Algorithm

For each unique value k of nums in increasing order, let's maintain the correct values of avoid and using, which represent the answer if we don't take or take k respectively.

If the new value k is adjacent to the previously largest value prev, then the answer if we must take k is (the point value of k) + avoid, while the answer if we must not take k is max(avoid, using). Similarly, if kis not adjacent to prev, the answer if we must take k is (the point value of k) + max(avoid, using), and the answer if we must not take k is max(avoid, using).

At the end, the best answer may or may not use the largest value in nums, so we return max(avoid, using).

Our demonstrated solutions showcase two different kinds of sorts: a library one, and a radix sort. For each language, the other kind of solution can be done without much difficulty, by using an array (Python) or HashMap (Java) respectively.

• Time Complexity (Python): $O(N \log N)$, where $N$ is the length of nums. We make a single pass through the sorted keys of $N$, and the complexity is dominated by the sorting step.
• Space Complexity (Python): $O(N)$, the size of our count.
• Time Complexity (Java): We performed a radix sort instead, so our complexity is $O(N+W)$ where $W$ is the range of allowable values for nums[i].
• Space Complexity (Java): $O(W)$, the size of our count.

  public int deleteAndEarn(int[] nums) {

    int[] count = new int[10001];

    for (int x : nums)

      count[x]++;

    int avoid = 0, using = 0, prev = -1;

    for (int k = 0; k <= 10000; ++k)

      if (count[k] > 0) {

        int m = Math.max(avoid, using);

        if (k - 1 != prev) {

          using = k * count[k] + m;

          avoid = m;

        } else {

          using = k * count[k] + avoid;

          avoid = m;

        }

        prev = k;

      }

    return Math.max(avoid, using);

  }

https://leetcode.com/problems/delete-and-earn/discuss/109895/JavaC++-Clean-Code-with-Explanation

1. If we sort all the numbers into buckets indexed by these numbers, this is essentially asking you to repetitively take an bucket while giving up the 2 buckets next to it. (the range of these numbers is [1, 10000])
2. The optimal final result can be derived by keep updating 2 variables skip_i, take_i, which stands for:
   skip_i : the best result for sub-problem of first (i+1) buckets from 0 to i, while you skip the ith bucket.
   take_i : the best result for sub-problem of first (i+1) buckets from 0 to i, while you take the ith bucket.
3. DP formula:
   take[i] = skip[i-1] + values[i];
skip[i] = Math.max(skip[i-1], take[i-1]);
take[i] can only be derived from: if you skipped the [i-1]th bucket, and you take bucket[i].
   skip[i] through, can be derived from either take[i-1] or skip[i-1], whatever the bigger;

 * for numbers from [1 - 10000], each has a total sum sums[i]; if you earn sums[i], you cannot earn sums[i-1] and sums[i+1]
 * kind of like house robbing. you cannot rob 2 connected houses.

    public int deleteAndEarn(int[] nums) {
        int n = 10001;
        int[] values = new int[n];
        for (int num : nums)
            values[num] += num;

        int take = 0, skip = 0;
        for (int i = 0; i < n; i++) {
            int takei = skip + values[i];
            int skipi = Math.max(skip, take);
            take = takei;
            skip = skipi;
        }
        return Math.max(take, skip);
    }

https://leetcode.com/problems/delete-and-earn/discuss/109871/Awesome-Python-4-liner-with-explanation-Reduce-to-House-Robbers-Question
The condition that we cannot pick adjacent values is similar to the House Robber question that we cannot rob adjacent houses. Simply pass points into the robfunction for a quick win

https://leetcode.com/problems/delete-and-earn/discuss/109889/Java-Easy-DP-Solution

Time: O(M+N)
Space: O(N)

M: the length of input array
N: the range of the value of each int element

public int deleteAndEarn(int[] nums) {
    int[] count = new int[10001];
    for(int n : nums){
        count[n] += n;
    }
    int[] dp = new int[10003];
    for(int i = 10000; i >= 0; i--) {
        dp[i] = Math.max(count[i] + dp[i + 2], dp[i + 1]);
    }
    return dp[0];
}

    public int deleteAndEarn(int[] nums) {
        int[] count = new int[10001];
        for (int x: nums) count[x]++;
        int avoid = 0, using = 0, prev = -1;

        for (int k = 0; k <= 10000; ++k) if (count[k] > 0) {
            int m = Math.max(avoid, using);
            if (k - 1 != prev) {
                using = k * count[k] + m;
                avoid = m;
            } else {
                using = k * count[k] + avoid;
                avoid = m;
            }
            prev = k;
        }
        return Math.max(avoid, using);
    }
class Solution(object):
    def deleteAndEarn(self, nums):
        count = collections.Counter(nums)
        prev = None
        avoid = using = 0
        for k in sorted(count):
            if k - 1 != prev:
                avoid, using = max(avoid, using), k * count[k] + max(avoid, using)
            else:
                avoid, using = max(avoid, using), k * count[k] + avoid
            prev = k
        return max(avoid, using)


下面这种解法直接使用sums数组来更新，而没有使用额外的变量。上面解法中没有讲解这个sums数组，这里的sums实际上相当于建立了数字和其总积分的映射，这里的总积分的计算方法是由数字乘以其出现次数得来的。由于题目中说了每个数字不会超过10000，所以sums的长度可以初始化为10001，然后遍历原数组，将遇到的数字都累加到该数字在数组中的位置上。然后从sums数组的第三个数字开始遍历，更新方法跟上面解法的思路很类似，当前的sums[i]值就等于前一个值sums[i-1]和前两个值sums[i-2]加上当前的sums[i]值中的较大值，其实思想就是在不拿当前数的积分，跟不拿前一个数的积分加上当前的积分之和，取二者中的较大值更新当前值sums[i]

    int deleteAndEarn(vector<int>& nums) {
        vector<int> sums(10001, 0);
        for (int num : nums) sums[num] += num;
        for (int i = 2; i < 10001; ++i) {
            sums[i] = max(sums[i - 1], sums[i - 2] + sums[i]);
        }
        return sums[10000];
    }