LeetCode 710 - Random Pick with Blacklist

https://leetcode.com/problems/random-pick-with-blacklist/

Given a blacklist B containing unique integers from [0, N), write a function to return a uniform random integer from [0, N)which is NOT in B.

Optimize it such that it minimizes the call to system’s Math.random().

Note:

1. 1 <= N <= 1000000000
2. 0 <= B.length < min(100000, N)
3. [0, N) does NOT include N. See interval notation.

Example 1:

Input: 
["Solution","pick","pick","pick"]
[[1,[]],[],[],[]]
Output: [null,0,0,0]

Example 2:

Input: 
["Solution","pick","pick","pick"]
[[2,[]],[],[],[]]
Output: [null,1,1,1]

Example 3:

Input: 
["Solution","pick","pick","pick"]
[[3,[1]],[],[],[]]
Output: [null,0,0,2]

Example 4:

Input: 
["Solution","pick","pick","pick"]
[[4,[2]],[],[],[]]
Output: [null,1,3,1]

Explanation of Input Syntax:

The input is two lists: the subroutines called and their arguments. Solution's constructor has two arguments, N and the blacklist B. pick has no arguments. Arguments are always wrapped with a list, even if there aren't any

X.
https://zxi.mytechroad.com/blog/math/leetcode-880-random-pick-with-weight/
Solution: Binary Search
Convert PDF to CDF
Uniformly sample a value s in [1, sum(weights)].
Use binary search to find first index such that PDF[index] >= s.
Time complexity: Init O(n), query O(logn)

Space complexity: O(n)
https://leetcode.com/problems/random-pick-with-blacklist/discuss/146545/Simple-Java-solution-with-Binary-Search

We need to first sort B. Let L denote its length.
Let M = N-L. We will generate numbers from the interval [0, M). Possible cases for a random value r are as follows;

• If it is in [0,B[0]), we can return r as it is.
• If it is in [B[0], B[1]-1), we can return r+1.
• If it is in [B[1]-1, B[2]-2), we can return r+2.
• ...
• If it is in [B[i]-i, B[i+1]-(i+1)), we can return r+i+1. Note that B[i] < r+i+1 < B[i+1], so it is safe.
• ...
• If it is in [B[L-1]-(L-1), M), we can return r+L. Note that B[L-1] < r+L < N, so it is safe.

So we will make a binary search on the interval boundaries (i.e. B[i]-(i+1)) and apply an offset according the the interval that the random number falls into int[] b;

    int M;
    
    public Solution(int N, int[] blacklist) {
        b = blacklist;
        this.M = N - b.length;
        
        Arrays.sort(b);
        for (int i = 0; i < b.length; i++) {
            b[i] -= (i+1);
        }
    }
    
    public int pick() {
        int r = (int) Math.floor(Math.random()*M);
        int index = Arrays.binarySearch(b, r);
        if (index < 0) {
            return r - (index+1);
        } else {
            // here is a bit tricky. we need to select the first boundary that 
            // matches, because the intervals degenerate if B[i+1]=B[i]+1.
            while (index > 0 && b[index-1] == r)
                index--;
            return r + index;
        }
    }

https://leetcode.com/problems/random-pick-with-blacklist/discuss/144441/Java-Binary-Search-Solution-O(BlogB)-for-constructor-and-O(logB)-for-pick()
https://zhanghuimeng.github.io/post/leetcode-710-random-pick-with-blacklist/

X. http://hehejun.blogspot.com/2018/07/leetcoderandom-pick-with-blacklist.html
假设blacklist的size为k，这道题第一个想法应该就是把所有不在blacklist里的数字重新map到[0, N - k)，的区间中。这样我们只需要生成一个在[0, N- k)范围中的数然后找对于map的原来的数字即可。但是鉴于这道题输入的范围，N可以达到10^9，我们是不可能开出这么大的数组的，所以我们要想其他的办法。
第一个想法就是时间换空间，既然没有那么多空间，我们在pick()多花点时间即可，比如我们可以生成一个[0, N - k)的数i，然后找第i个不在blacklist里的数返回。但是这样的话显然每次pick的时间复杂度变为了O(N)，这是我们不能接受的。
有的时候我们需要从另一个角度思考，既然我们存不下N的范围，k的范围我们总是可以存的下的。对于生成的在[0, N - k)中的数i，其可能在blacklist当中，但是如果对于所有在[0, N - k)范围中并且在blacklist当中的数，我们重新map到[N - k, N)范围中另一个不在blacklist的数(显然这两个集合的size是相等的，我们可以做到一一映射)。我们仍然可以达到我们之前所说的效果，并且这个在空间上是完全可行的。
时间复杂度的话，我们要对blacklist进行sort，所以constructor的时间复杂度为O(N * log N)，pick的话为O(1)。空间复杂度O(k)
https://leetcode.com/problems/random-pick-with-blacklist/discuss/144624/Java-O(B)-O(1)-HashMap

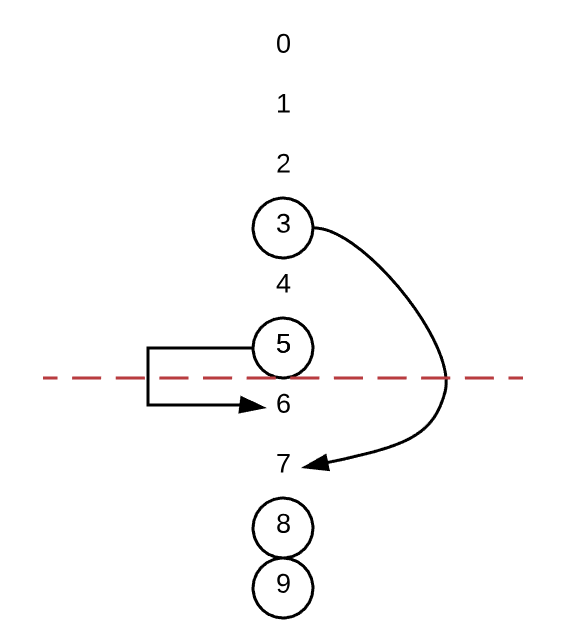
Suppose N=10, blacklist=[3, 5, 8, 9], re-map 3 and 5 to 7 and 6.

    // N: [0, N)
    // B: blacklist
    // B1: < N
    // B2: >= N
    // M: N - B1
    int M;
    Random r;
    Map<Integer, Integer> map;

    public Solution(int N, int[] blacklist) {
        map = new HashMap();
        for (int b : blacklist) // O(B)
            map.put(b, -1);
        M = N - map.size();
        
        for (int b : blacklist) { // O(B)
            if (b < M) { // re-mapping
                while (map.containsKey(N - 1))
                    N--;
                map.put(b, N - 1);
                N--;
            }
        }
        
        r = new Random();
    }
    
    public int pick() {
        int p = r.nextInt(M);
        if (map.containsKey(p))
            return map.get(p);
        return p;
    }

X. Out of memory
http://www.programmersought.com/article/756569193/
The number of random numbers in the final result is definitelyN-len(blacklist), so we have to choose the last random value, one is to map the value in the blacklist to the whitelist
The number of random numbers in the result isN-len(blacklist), then we must first take the array [0, N] beforeN-len(blacklist)Elements, but before thisN-len(blacklist)What if there are elements in the blacklist? We use a pointer to scan the array from back to front. If the latter value is not in the blacklist and the previous value is in the blacklist, replace the previous one with the following value.
After the above operation, we will range from randomNShrinked toN- len(blacklist)In the range of size, save it with a map, the key is1~N-len(blacklist), the value is the number in the white list

   def __init__(self, N, blacklist):
        """
        :type N: int
        :type blacklist: List[int]
        """
        self.map = {}
        for i in blacklist:
            self.map[i] = 1
        self.M = N - len(blacklist)
        for i in blacklist:
            if i < self.M:
                N = N-1
                while N in self.map:
                    N -= 1
                self.map[i] = N
        for i in range(self.M):
            if i not in self.map:
                self.map[i] = i
    def pick(self):
        """
        :rtype: int
        """
        import  random
        return self.map[random.randint(0,self.M-1)]