TopCoder QuickSums – SRM 197 Div 2

https://community.topcoder.com/stat?c=problem_statement&pm=2829&rd=5072

Given a string of digits, find the minimum number of additions required for the string to equal some target number. Each addition is the equivalent of inserting a plus sign somewhere into the string of digits. After all plus signs are inserted, evaluate the sum as usual. For example, consider the string "12" (quotes for clarity). With zero additions, we can achieve the number 12. If we insert one plus sign into the string, we get "1+2", which evaluates to 3. So, in that case, given "12", a minimum of 1 addition is required to get the number 3. As another example, consider "303" and a target sum of 6. The best strategy is not "3+0+3", but "3+03". You can do this because leading zeros do not change the result. Write a class QuickSums that contains the method minSums, which takes a String numbers and an int sum. The method should calculate and return the minimum number of additions required to create an expression from numbers that evaluates to sum. If this is impossible, return -1. Definition      Class: QuickSums Method: minSums Parameters: String, int Returns: int Method signature: int minSums(String numbers, int sum) (be sure your method is public)      Constraints - numbers will contain between 1 and 10 characters, inclusive. - Each character in numbers will be a digit. - sum will be between 0 and 100, inclusive. Examples 0)      "99999" 45 Returns: 4 In this case, the only way to achieve 45 is to add 9+9+9+9+9. This requires 4 additions. 1)      "1110" 3 Returns: 3 Be careful with zeros. 1+1+1+0=3 and requires 3 additions. 2)      "0123456789" 45 Returns: 8 3)      "99999" 100 Returns: -1 4)      "382834" 100 Returns: 2 There are 3 ways to get 100. They are 38+28+34, 3+8+2+83+4 and 3+82+8+3+4. The minimum required is 2. 5)      "9230560001" 71 Returns: 4 This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

https://tictactoed.wordpress.com/2013/07/16/quicksums-topcoder/

Problem (abridged): Given a string numbers of digits (such as “12” or “28475”) find the minimum number of insertions of addition signs into the string so that the resulting expression evaluates to a given number sum. If this is not possible, return -1. Resulting terms in the expression are not affected by leading zeros (so 047 reads as 47).

numbers has at most 10 characters (all digits), and sum is at most 100.

Examples:

1) numbers = “1583”, sum = 161. The minimum is 1; we can just do 158+3=161.

2) numbers = “26007”, sum = 15. The minimum is 2; we do not do 2+6+0+0+7 but instead 2+6+007=2+6+7.

3) numbers = “999999”, sum = 8. Obviously impossible, so -1.

Solution: Since numbers has at most 10 digits, at most 9 spaces are available for plus signs and we can just brute force, since 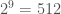 is very small. There seems to also be a dynamic programming solution, which I didn’t think of.

So many stumbles in this problem:

• When getting rid of the leading zeros in the expression fragments the first time, I just copied over all the nonzero characters. This is a problem if the string is something like “000”.
• Sometimes the sum of the expression being tested doesn’t fit in a 32-bit integer. Since sum isn’t supposed to be more than 100, I just broke if any of the fragments (without leading zeros!) were longer than 3 characters.
• When doing the above, I accidentally put the <testing longer than 3  characters> before removing the leading zeros, which is a problem if the string is something like “0004”, which is clearly not more than 100.

  static int n, min, des, numplus;

  static boolean plus[];

  static String nums;

  public int minSums(String numbers, int sum) {

    n = numbers.length();

    des = sum;

    numplus = 0;

    nums = new String(numbers);

    plus = new boolean[n - 1];

    min = n;

    genPlus(0);

    if (min < n)

      return min;

    return -1;

  }

  void genPlus(int i) {

    if (i + 1 < n) {

      plus[i] = true;

      numplus++;

      genPlus(i + 1);

      plus[i] = false;

      numplus--;

      genPlus(i + 1);

    } else {

      String manip = "";

      manip += nums.substring(0, 1);

      for (int j = 1; j < n; j++) {

        if (plus[j - 1])

          manip += "+";

        manip += nums.substring(j, j + 1);

      }

      // compute sum

      int s = 0;

      StringTokenizer k = new StringTokenizer(manip, "+");

      while (k.hasMoreTokens()) {

        String st = k.nextToken();

        for (int a = 0; a < st.length(); a++) {

          if (st.charAt(a) != '0') {

            st = st.substring(a);

            break;

          }

        }

        if (st.charAt(0) == '0')

          st = "0";

        if (st.length() > 3) {

          s = -1;

          break;

        }

        s += Integer.parseInt(st);

      }

      if (s == des) {

        min = Math.min(min, numplus);

        System.out.println(manip);

      }

    }

  }

https://blog.csdn.net/u013113958/article/details/38852631

 给一个字符串，可以在中间添加‘+’,使得和为给定的数（前导0为合法的数），返回最小的加号添加个数，没有方案，返回-1。

 ”99999“   45
答案：45   “9+9+9+9+9”
解法：
状压枚举所有情况。就ok了。
看了官方的说法，暴力可做，还想着什么暴力（难道是很暴力的那种做法嘛-组合数那种的呢），真的好巧妙，状压枚举就可以了（主要是太菜了）。最大就是1<<9(才几百，没关系的了)。
官方说法，矩阵乘法，DP均可做的。

https://community.topcoder.com/tc?module=Static&d1=match_editorials&d2=srm197

This problem is very flexible when it comes to solving it. Memoization, dynamic programming, and brute force are all good options here. With at most 10 digits, there are at most 2⁹ ways to insert plus signs into the string. Therefore, there are at most 2⁹ possibilities to consider. We can use recursion to go through all possibilities and keep track of the minimum number of additions required. The only thing to watch out for is not parsing numbers so large that they do not fit into an integer type. To avoid this problem altogether, we may use a 64-bit integer type. As a challenge, you may write a dynamic programming solution that uses the same principles as the Matrix Multiplication problem.

https://topcoder.g.hatena.ne.jp/caligue/20090905/1252116709
http://code-jedi.chintanghate.me/2014/12/01/quicksums/

    int minSums(string numbers, int sum) {
        int result = INT_MAX;
        D = numbers.length();
        for (int i = 0; i < power2(D-1); i++) {
            bitset<9> plus(i);
            int thisSum = getSum(numbers, plus);
            if (thisSum == sum) 
                result = min(result, (int)plus.count());
        }
        if (result == INT_MAX) return -1;
        else return result;
    }
private:
    int D;
    int power2(int d) {
        int ret = 1;
        while (d-- > 0) ret *= 2;
        return ret;
    }
    int getSum(const string& nums, const bitset<9>& plus) {
        int sum = 0;
        int pre = 0;
        for (int i = 0; i < D-1; i++) {
            if (plus[i]) {
                sum += atoi(nums.substr(pre,i-pre+1).c_str());
                pre = i+1;
            }
        }
        sum += atoi(nums.substr(pre,D-pre).c_str());
        return sum;
    }

X. DP
http://code.antonio081014.com/2011/10/srm197.html
This problem is a nice chance to practice my dynamic programming skill. The dp[i][j] represents the minimum number of plus should be used by using first i digits with the sum j.
dp[i] [j] = min{dp[i][j], dp[k-1][j - tmpSum]+1}, which tmpSum is the number represented by the digits from k to i.

    public int minSums(String numbers, int sum) {
        int N = numbers.length();
        long[][] dp = new long[N][sum + 1];
        for (int i = 0; i < N; i++) {
            for (int j = 0; j <= sum; j++) {
                dp[i][j] = Long.MAX_VALUE - 1;
            }
        }
        for (int i = 0; i < N; i++) {
            long tmp = Long.parseLong(numbers.substring(0, i + 1));
            if (tmp <= sum)
                dp[i][(int) tmp] = 0;
            else
                break;
        }
        // for (int i = 0; i < N; i++) {
        // for (int j = 0; j <= sum; j++) {
        // System.out.print(dp[i][j]);
        // System.out.print(", ");
        // }
        // System.out.println();
        // }
        // System.out.println();
        for (int i = 0; i < N; i++) {
            for (int k = 1; k <= i; k++) {
                long tmp = Long.parseLong(numbers.substring(k, i + 1));
                if (tmp > sum)
                    continue;
                for (int j = 0; j <= sum; j++) {
                    if (j >= tmp)
                        dp[i][j] = Math.min(dp[i][j],
                                dp[k - 1][j - (int) tmp] + 1);
                }
            }
        }
        // for (int i = 0; i < N; i++) {
        // for (int j = 0; j <= sum; j++) {
        // System.out.print(dp[i][j]);
        // System.out.print(", ");
        // }
        // System.out.println();
        // }
        if (dp[N - 1][sum] == Long.MAX_VALUE - 1)
            return -1;
        return (int) dp[N - 1][sum];
    }


dp[i][j] = min(dp[i][j],dp[i + k][sum - numbers.substr(i,k)] + 1)
http://greeness2008.blogspot.com/2008/09/memoij-min-memoik-memok1j.html
memo[i][j] = min ( memo[i][k] + memo[k+1][j] )
用类似这一recurrence的题非常多，在这汇总一下
topCoder: QuickSums
topCoder: ShortPalindromes
topCoder: TreePlanting
topCoder: SentenceDecomposition

INPUT: i, j, sum
for all  i <= k <= j   take out substring(i,k) from sum   try d[k+1][j] = solve(substring(k+1,j), sum - substring(i,k)); end for d[i][j] = min (1+d[k+1][j])         k=i...j

边缘情况注意一下，如果d[i][j]整体已经等于sum，直接返回，不用1+res

int memo[12][12][102];
void checkmin(int &a, int b) {
if(b < a) a = b;
}
int solve(string numbers, int i, int j, int s) {
if(memo[i][j][s] >= 0) return memo[i][j][s];
if(i == j) {
if (numbers[i]-'0' == s) return memo[i][j][s] = 0;
else return memo[i][j][s] = INF;
}
// the whole word match!
if(atoi(numbers.substr(i, j-i+1).c_str()) == s) return memo[i][j][s] = 0;
int res = INF;
for(int k = i; k < j; ++k) {
int left = atoi(numbers.substr(i,k-i+1).c_str());
if(left <= s){
//cout << numbers.substr(k+1, j-k+1) << "->" << s-left << endl;
int sol = 1+solve(numbers, k+1, j, s-left);
//cout << numbers.substr(k+1, j-k+1) << " (" << sol <<")" << endl;
checkmin(res, sol);
}
}
return memo[i][j][s] = res;
}

int QuickSums::minSums(string numbers, int sum) {
memset(memo, -1, sizeof(memo));
int res = solve(numbers, 0, numbers.length()-1, sum);
if(res == INF) return -1;
return res;
}

https://github.com/Fuco1/topcoder/blob/master/QuickSums/src/main/java/me/QuickSums.java
    // dynamic programming
    public static int minSums(String num, int s) {
        Map<String, int[]> t = new HashMap<String, int[]>();
        for (int l = 1; l <= num.length(); l++) {
            for (int i = 0; i + l <= num.length(); i++) {
                String c = num.substring(i, i + l);
                long ci = Long.parseLong(c);
                int[] col = new int[s+1];
                for (int cs = 0; cs <= s; cs++) {
                    col[cs] = MAX;
                    if (cs == ci) col[cs] = 0;
                    else {
                        int min = MAX;
                        for (int k = 1; k < c.length(); k++) {
                            long rest = cs - Long.parseLong(c.substring(0, k));
                            if (0 <= rest && rest <= cs) {
                                int csteps = t.get(c.substring(k))[(int)rest];
                                if (min > csteps) min = csteps;
                            }
                        }
                        col[cs] = 1 + min;
                    }
                }
                //System.out.prlongln(c + ": " + Arrays.toString(col));
                t.put(c, col);
            }
        }
        int re = t.get(num)[s];
        return re >= MAX ? -1 : re;
    }