Massive Algorithms: Sparse Table

https://mayanknatani.wordpress.com/2013/07/15/range-minimum-query/

Time Complexity : Construction O(NlogN) Query O(1) <O(NlogN),O(1)>
To get an asymptotically faster time bound, we need to think something out of the box then to just look into the trivial comparisons based algorithms. The next algorithm will take use of a special data structure known as Sparse Tables. Sparse tables stores the information from one index ‘i’ to the some index ‘j’ which is at a specific distance from ‘i’.

Here we use Sparse table to store the minimum of the elements between index ‘i’ to i+’2^j’. It can be better understood with the help of an example :
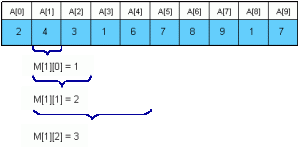
let us say, A = [2,4,3,1,6,7,8,9,1,7]
and the sparse table be two dimensional Array M( N*(log(N)+1) )

To compute M[i][j] we use dynamic programming

             M[i][j-1]  if(A[M[i][j-1]]<= A[M[i+2^(j-1)-1][j-1]])
M[i][j] = 
             M[i+2^(j-1)-1][j-1]

Now after precomputation of the table ‘M’ The RMQ can be solved in O(1) as follows :
let k = log(j-i+1)

             A[M[i][k]]  if(A[M[i][k]]<=A[M[j-2^k+1][k]])
RMQ(i,j) = 
             A[M[j-2^k+1][k]]

int M[MAXN][MAXLOGN];

void Compute_ST(int A[],int N){

    int i,j;

    for(i=0;i&lt;N;i++)

        M[i][0]=i;

    for(j=1;1&lt;&lt;j &lt;=N ;j++){

        for(i=0;i+(1&lt;&lt;(j-1))&lt;N;i++){

            if(A[M[i][j-1]]&lt;=A[M[i+(1&lt;&lt;(j-1))][j-1]])

                M[i][j]=M[i][j-1];

            else

                M[i][j]=M[i+(1&lt;&lt;(j-1))][j-1];

}

}

}

int RMQ(int A[],int s,int e){

    int k=e-s;

    k=31-__builtin_clz(k+1); // k = log(e-s+1)

    if(A[M[s][k]]&lt;=A[M[e-(1&lt;&lt;k)+1][k]])

        return A[M[s][k]];

    return A[M[e-(1&lt;&lt;k)+1][k]];

}

https://comeoncodeon.wordpress.com/2009/04/18/range-minimum-query/

A better approach is to preprocess RMQ for sub arrays of length 2^k using dynamic programming. We will keep an array preProcess[0, N-1][0, logN] where preProcess[i][j] is the index of the minimum value in the sub array starting at i having length 2^j. For example :

A[0]	A[1]	A[2]	A[3]	A[4]	A[5]
2	4	3	1	6	7

For the above array the preProcess[1][0] = 1, preProcess[1][1]=2,preProcess[1][2]=3 and so on. Specifically, we find the minimum in a block of size 2^j by comparing the two minima of its two constituent blocks of size 2^j-1. More formally, preProcess[i, j] = preProcess[i, j -1] if A[preProcess[i, j -1]] <= A[preProcess[i+2^j-1, j -1]] and preProcess[i, j] = preProcess[i+2^j-1, j -1] otherwise.

Once we have these values preprocessed, let’s show how we can use them to calculate RMQ(i, j). The idea is to select two blocks that entirely cover the interval [i..j] and find the minimum between them. We select two overlapping blocks that entirely cover the subrange: let 2k be the size of the largest block that fits into the range from i to j, that is let k = log(j – i). Then rmq(i, j) can be computed by comparing the minima of the following two blocks: i to i + 2^k – 1 (preProcess(i, k)) and j – 2^k + 1 to j (preProcess(j –2^k +1, k)). These values have already been computed, so we can find the RMQ in constant time.

https://sites.google.com/site/indy256/algo/sparse_table_rmq

public class RmqSparseTable {

  int[] logTable;
  int[][] rmq;
  int[] a;

  public RmqSparseTable(int[] a) {
    this.a = a;
    int n = a.length;

    logTable = new int[n + 1];
    for (int i = 2; i <= n; i++)
      logTable[i] = logTable[i >> 1] + 1;

    rmq = new int[logTable[n] + 1][n];

    for (int i = 0; i < n; ++i)
      rmq[0][i] = i;

    for (int k = 1; (1 << k) < n; ++k) {
      for (int i = 0; i + (1 << k) <= n; i++) {
        int x = rmq[k - 1][i];
        int y = rmq[k - 1][i + (1 << k - 1)];
        rmq[k][i] = a[x] <= a[y] ? x : y;
      }
    }
  }

  public int minPos(int i, int j) {
    int k = logTable[j - i];
    int x = rmq[k][i];
    int y = rmq[k][j - (1 << k) + 1];
    return a[x] <= a[y] ? x : y;
  }

  public static void main(String[] args) {
    int[] a = { 1, 5, -2, 3 };
    RmqSparseTable st = new RmqSparseTable(a);

    System.out.println(2 == st.minPos(0, 3));
  }
}

https://www.geeksforgeeks.org/sparse-table/
https://gist.github.com/Jangwa/8670985

Sparse Table - Range Min Query

Labels

Popular Posts