PT07X - Vertex Cover Problem

https://www.spoj.com/problems/PT07X/

You are given an unweighted, undirected tree. Write a program to find a vertex set of minimum size in this tree such that each edge has as least one of its end-points in that set.

Input

The first line of the input file contains one integer N --- number of nodes in the tree (0 < N <= 100000). Next N-1 lines contain N-1 edges of that tree --- Each line contains a pair (u, v) means there is an edge between node u and node v (1 <= u,v <= N).

Output

Print number of nodes in the satisfied vertex set on one line.

Example 1

Input:
3
1 2
1 3

Output:
1

Explanation:
The set can be {1}

Example 2

Input:
3
1 2
2 3

Output:
1

Explanation:
The set can be {2}

https://www.geeksforgeeks.org/vertex-cover-problem-set-2-dynamic-programming-solution-tree/

A vertex cover of an undirected graph is a subset of its vertices such that for every edge (u, v) of the graph, either ‘u’ or ‘v’ is in vertex cover. Although the name is Vertex Cover, the set covers all edges of the given graph.
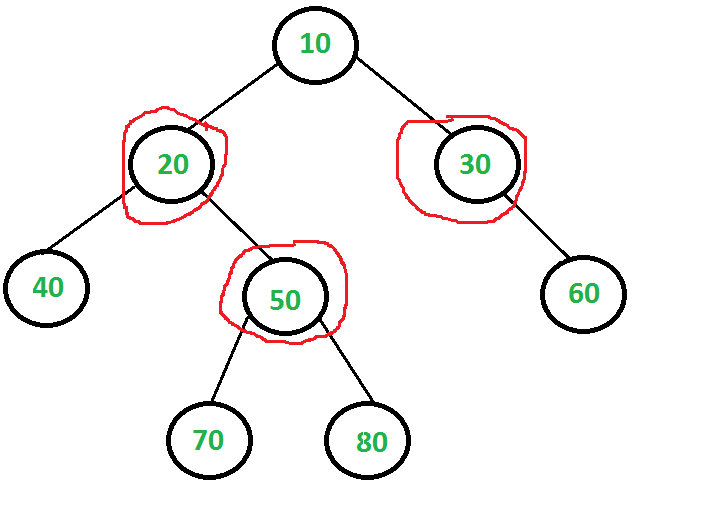
The problem to find minimum size vertex cover of a graph is NP complete. But it can be solved in polynomial time for trees. In this post a solution for Binary Tree is discussed. The same solution can be extended for n-ary trees.

1) Root is part of vertex cover: In this case root covers all children edges. We recursively calculate size of vertex covers for left and right subtrees and add 1 to the result (for root).

2) Root is not part of vertex cover: In this case, both children of root must be included in vertex cover to cover all root to children edges. We recursively calculate size of vertex covers of all grandchildren and number of children to the result (for two children of root).

http://www.voidcn.com/article/p-ehrveykf-tk.html

https://github.com/anmolvarshney05/SPOJ-Solutions/blob/master/SPOJ%20PT07X%20-%20Vertex%20Cover.cpp

http://one-problem-a-day.blogspot.com/2011/07/spoj-pt07x-vertex-cover.html

#define min(a,b) (((a)<(b))?(a):(b))
#define rep(i,n) for(i=0;i<(n);i++)
#define MAXN 100000

vector<int> adj[MAXN+2];
int n;
int dp[MAXN+2][2];

int go(int cur, int parent, bool isParentCovered) {
 if(dp[cur][isParentCovered] != -1) return dp[cur][isParentCovered];
 int &ret = dp[cur][isParentCovered];
 ret = 0;
 int i, r;
 if(isParentCovered) {
  rep(i, adj[cur].size()) if(adj[cur][i] != parent) {
   ret += go(adj[cur][i], cur, false);
  }

  r = 1;
  rep(i, adj[cur].size()) if(adj[cur][i] != parent) {
   r += go(adj[cur][i], cur, true) ;
  }
  ret = min(ret, r);
 }
 else {
  ret = 1;
  rep(i, adj[cur].size()) if(adj[cur][i] != parent) {
   ret += go(adj[cur][i], cur, true) ;
  }
 }
 return ret;
}

int main() {
 int i,u,v;
 int r1,r2;
 while(scanf(" %d",&n) == 1) {
  for(i=1;i<=n;i++) adj[i].clear();
  for(i=1;i<n;i++) {
   scanf(" %d %d",&u,&v);
   adj[u].push_back(v);
   adj[v].push_back(u);
  }
  memset(dp,-1,sizeof(dp));
  r1 = 1;
  rep(i,adj[1].size()) r1 += go(adj[1][i], 1, true);
  r2 = 0;
  rep(i, adj[1].size()) r2 += go(adj[1][i], 1, false);
  printf("%d\n",min(r1,r2));
 }
 return 0;
}

struct node

{

    int data;

    int vc;

    struct node *left, *right;

};

  

// A memoization based function that returns size of the minimum vertex cover.

int vCover(struct node *root)

{

    // The size of minimum vertex cover is zero if tree is empty or there

    // is only one node

    if (root == NULL)

        return 0;

    if (root->left == NULL && root->right == NULL)

        return 0;

  

    // If vertex cover for this node is already evaluated, then return it

    // to save recomputation of same subproblem again.

    if (root->vc != 0)

        return root->vc;

  

    // Calculate size of vertex cover when root is part of it

    int size_incl = 1 + vCover(root->left) + vCover(root->right);

  

    // Calculate size of vertex cover when root is not part of it

    int size_excl = 0;

    if (root->left)

      size_excl += 1 + vCover(root->left->left) + vCover(root->left->right);

    if (root->right)

      size_excl += 1 + vCover(root->right->left) + vCover(root->right->right);

  

    // Minimum of two values is vertex cover, store it before returning

    root->vc =  min(size_incl, size_excl);

  

    return root->vc;

}

Time complexity of the above naive recursive approach is exponential. It should be noted that the above function computes the same subproblems again and again. For example, vCover of node with value 50 is evaluated twice as 50 is grandchild of 10 and child of 20.

// The function returns size of the minimum vertex cover

int vCover(struct node *root)

{

    // The size of minimum vertex cover is zero if tree is empty or there

    // is only one node

    if (root == NULL)

        return 0;

    if (root->left == NULL && root->right == NULL)

        return 0;

  

    // Calculate size of vertex cover when root is part of it

    int size_incl = 1 + vCover(root->left) + vCover(root->right);

  

    // Calculate size of vertex cover when root is not part of it

    int size_excl = 0;

    if (root->left)

      size_excl += 1 + vCover(root->left->left) + vCover(root->left->right);

    if (root->right)

      size_excl += 1 + vCover(root->right->left) + vCover(root->right->right);

  

    // Return the minimum of two sizes

    return min(size_incl, size_excl);

}