https://leetcode.com/problems/k-th-smallest-prime-fraction/
http://www.cnblogs.com/grandyang/p/9135156.html
其实这道题比较经典的解法是用二分搜索法Binary Search,这道题使用的二分搜索法是博主归纳总结帖LeetCode Binary Search Summary 二分搜索法小结中的第四种,即二分法的判定条件不是简单的大小关系,而是可以抽离出子函数的情况,下面我们来看具体怎么弄。这种高级的二分搜索法在求第K小的数的时候经常使用,比如 Kth Smallest Element in a Sorted Matrix,Kth Smallest Number in Multiplication Table,和 Find K-th Smallest Pair Distance 等。思路都是用mid当作candidate,然后统计小于mid的个数cnt,和K进行比较,从而确定折半的方向。这道题也是如此,mid为候选的分数值,刚开始时是0.5,然后我们需要统计出不大于mid的分数都个数cnt,同时也需要找出最接近mid的分数,当作返回的候选值,因为一旦cnt等于K了,直接将这个候选值返回即可,否则如果cnt小于K,说明我们应该增大一些mid,将left赋值为mid,反之如果cnt大于K,我们需要减小mid,将right赋值为mid
上面这个算法的问题在于当K特别大的时候,算法的时间复杂度其实还挺高的。另外一种解决思路就是采用二分查找。还是以题目中给出的[1,2,3,5]为例俩说明问题:
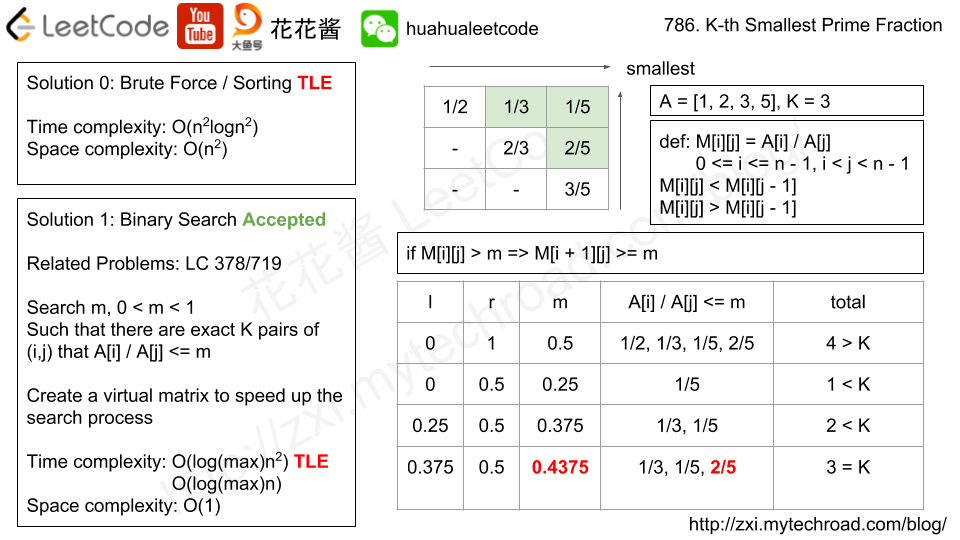
我们初始化left = 0, right = 1,作为二分查找的边界。然后每次取left和right的中间值,再分别计算每行中有多少个值小于等于mid。最后将所有行中小于等于mid的分数的个数加起来,记为count。如果发现count小于K,那么说明mid的取值过小,所以修改左边界;否则修改右边界。这样当count的个数刚好为K的时候,我们取小于等于mid的所有分数中的最大值,即为第K大的分数。二分查找法的空间复杂度为O(1),时间复杂度为O(log(r)n^2),其中r是left和right之间的差值。可以发现这个算法的时间复杂度与K无关。由于K一般情况下下是O(n^2)量级的,所以二分查找的时间复杂度还是要好于基于优先队列的方法。
https://zxi.mytechroad.com/blog/two-pointers/leetcode-786-k-th-smallest-prime-fraction/
Binary search m, 0 < m < 1, such that there are exact k pairs of (i, j) that A[i] / A[j] < m
Time complexity: O(n*C) C <= 31
https://leetcode.com/problems/k-th-smallest-prime-fraction/discuss/115505/Java-14ms-O(n*C)-C-is-the-number-of-iteration-C-30-is-enough
X. Priority Queue
https://blog.csdn.net/magicbean2/article/details/79733065
1、优先队列:
我们先找规律,观察题目中给出的的例子[1, 2, 3, 5],很容易知道:
1/5 < 1/3 < 1/2
2/5 < 2/3
3/5
也就是说,对于每个A[i],如果以它为分子,则分母从A.back()到A[i+1],与A[i]构成的分数呈严格递增序列。在这种情况下,我们可以通过优先队列来依次取出K个数,那么其取出的第K个数,就是我们所求。我们定义一个priority_queue<pair<double, pair<int, int>>>,其中pair中的第一个即为两个整数构成的分数,第二个分别为分子和分母在A中索引。以上面的例子来说明,我们在初始化的时候,将1/5, 2/5, 3/5分别加入优先队列中,然后每当取出最小元素,假如为A[p]/A[q],我们就检查p是否小于q-1,如果是,则说明A[p]/A[q-1]也是合乎要求的分数,所以就将A[p]/A[q-1]也加入优先队列中。
在实现中,为了保证最小的值首先被从pq中取出,我们将分数取负作为优先队列中的key。算法的空间复杂度为O(n),时间复杂度为O(Klogn)。
https://leetcode.com/problems/k-th-smallest-prime-fraction/discuss/116107/Java-Better-than-O(NlogN)-it-can-be-O(KlogK)
https://leetcode.com/problems/k-th-smallest-prime-fraction/discuss/115531/C%2B%2B-9lines-priority-queue
http://bookshadow.com/weblog/2018/02/18/leetcode-k-th-smallest-prime-fraction/
X. https://leetcode.com/problems/k-th-smallest-prime-fraction/discuss/115819/Summary-of-solutions-for-problems-%22reducible%22-to-LeetCode-378
X. https://blog.csdn.net/u014688145/article/details/79335163
https://leetcode.com/problems/k-th-smallest-prime-fraction/discuss/115819/Summary-of-solutions-for-problems-%22reducible%22-to-LeetCode-378
This is essentially a Young tableau. Now, given any fraction in the table, we can find its rank in
A sorted list
A contains 1, plus some number of primes. Then, for every p < q in the list, we consider the fraction p/q.
What is the
K-th smallest fraction considered? Return your answer as an array of ints, where answer[0] = p and answer[1] = q.Examples: Input: A = [1, 2, 3, 5], K = 3 Output: [2, 5] Explanation: The fractions to be considered in sorted order are: 1/5, 1/3, 2/5, 1/2, 3/5, 2/3. The third fraction is 2/5. Input: A = [1, 7], K = 1 Output: [1, 7]
Note:
Awill have length between2and2000.- Each
A[i]will be between1and30000. Kwill be between1andA.length * (A.length - 1) / 2
Binary search m, 0 < m < 1, such that there are exact k pairs of (i, j) that A[i] / A[j] < m
Time complexity: O(n*C) C <= 31
public int[] kthSmallestPrimeFraction(int[] A, int K) {
final int n = A.length;
double l = 0;
double r = 1.0;
while (l < r) {
double m = (l + r) / 2;
double max_f = 0.0;
int total = 0;
int p = 0;
int q = 0;
for (int i = 0, j = 1; i < n - 1; ++i) {
while (j < n && A[i] > m * A[j]) ++j;
if (n == j) break;
total += (n - j);
final double f = (double)A[i] / A[j];
if (f > max_f) {
p = i;
q = j;
max_f = f;
}
}
if (total == K)
return new int[]{A[p], A[q]};
else if (total > K)
r = m;
else
l = m;
}
return new int[] {};
}
其实这道题比较经典的解法是用二分搜索法Binary Search,这道题使用的二分搜索法是博主归纳总结帖LeetCode Binary Search Summary 二分搜索法小结中的第四种,即二分法的判定条件不是简单的大小关系,而是可以抽离出子函数的情况,下面我们来看具体怎么弄。这种高级的二分搜索法在求第K小的数的时候经常使用,比如 Kth Smallest Element in a Sorted Matrix,Kth Smallest Number in Multiplication Table,和 Find K-th Smallest Pair Distance 等。思路都是用mid当作candidate,然后统计小于mid的个数cnt,和K进行比较,从而确定折半的方向。这道题也是如此,mid为候选的分数值,刚开始时是0.5,然后我们需要统计出不大于mid的分数都个数cnt,同时也需要找出最接近mid的分数,当作返回的候选值,因为一旦cnt等于K了,直接将这个候选值返回即可,否则如果cnt小于K,说明我们应该增大一些mid,将left赋值为mid,反之如果cnt大于K,我们需要减小mid,将right赋值为mid
上面这个算法的问题在于当K特别大的时候,算法的时间复杂度其实还挺高的。另外一种解决思路就是采用二分查找。还是以题目中给出的[1,2,3,5]为例俩说明问题:
我们初始化left = 0, right = 1,作为二分查找的边界。然后每次取left和right的中间值,再分别计算每行中有多少个值小于等于mid。最后将所有行中小于等于mid的分数的个数加起来,记为count。如果发现count小于K,那么说明mid的取值过小,所以修改左边界;否则修改右边界。这样当count的个数刚好为K的时候,我们取小于等于mid的所有分数中的最大值,即为第K大的分数。二分查找法的空间复杂度为O(1),时间复杂度为O(log(r)n^2),其中r是left和right之间的差值。可以发现这个算法的时间复杂度与K无关。由于K一般情况下下是O(n^2)量级的,所以二分查找的时间复杂度还是要好于基于优先队列的方法。
vector<int> kthSmallestPrimeFraction(vector<int>& A, int K) { double left = 0, right = 1; int p = 0, q = 1, cnt = 0, n = A.size(); while (true) { double mid = left + (right - left) / 2.0; cnt = 0; p = 0; for (int i = 0, j = 0; i < n; ++i) { while (j < n && A[i] > mid * A[j]) ++j; cnt += n - j; if (j < n && p * A[j] < q * A[i]) { p = A[i]; q = A[j]; } } if (cnt == K) return {p, q}; else if (cnt < K) left = mid; else right = mid; } }
Binary search m, 0 < m < 1, such that there are exact k pairs of (i, j) that A[i] / A[j] < m
Time complexity: O(n*C) C <= 31
public int[] kthSmallestPrimeFraction(int[] A, int K) {
final int n = A.length;
double l = 0;
double r = 1.0;
while (l < r) {
double m = (l + r) / 2;
double max_f = 0.0;
int total = 0;
int p = 0;
int q = 0;
for (int i = 0, j = 1; i < n - 1; ++i) {
while (j < n && A[i] > m * A[j]) ++j;
if (n == j) break;
total += (n - j);
final double f = (double)A[i] / A[j];
if (f > max_f) {
p = i;
q = j;
max_f = f;
}
}
if (total == K)
return new int[]{A[p], A[q]};
else if (total > K)
r = m;
else
l = m;
}
return new int[] {};
}
https://leetcode.com/problems/k-th-smallest-prime-fraction/discuss/115505/Java-14ms-O(n*C)-C-is-the-number-of-iteration-C-30-is-enough
int p, q;
// O(n) for each check.
boolean check(double mid, int[] A, int K) {
int n = A.length;
int p1 = 0, q1 = 0;
int total = 0;
for (int i = 0, j = 0; i < n; i++) {
for (; j < n; j++) { // j will not backtrack.
if (i < j && A[i] < A[j] * mid) {
if (p1 == 0 || p1 * A[j] < A[i] * q1) {
p1 = A[i];
q1 = A[j];
}
break;
}
}
total += n - j;
}
if (total <= K) {
if (p == 0 || p * q1 < p1 * q) {
p = p1;
q = q1;
}
return true;
} else {
return false;
}
}
public int[] kthSmallestPrimeFraction(int[] A, int K) {
p = q = 0;
double low = 0.0;
double high = 1.0;
// Around 30 times of iteration
while (high - low > 1e-8) {
double mid = (low + high) / 2.0;
if (check(mid, A, K)) {
low = mid;
} else {
high = mid;
}
}
return new int[] { p, q };
}X. Priority Queue
https://blog.csdn.net/magicbean2/article/details/79733065
1、优先队列:
我们先找规律,观察题目中给出的的例子[1, 2, 3, 5],很容易知道:
1/5 < 1/3 < 1/2
2/5 < 2/3
3/5
也就是说,对于每个A[i],如果以它为分子,则分母从A.back()到A[i+1],与A[i]构成的分数呈严格递增序列。在这种情况下,我们可以通过优先队列来依次取出K个数,那么其取出的第K个数,就是我们所求。我们定义一个priority_queue<pair<double, pair<int, int>>>,其中pair中的第一个即为两个整数构成的分数,第二个分别为分子和分母在A中索引。以上面的例子来说明,我们在初始化的时候,将1/5, 2/5, 3/5分别加入优先队列中,然后每当取出最小元素,假如为A[p]/A[q],我们就检查p是否小于q-1,如果是,则说明A[p]/A[q-1]也是合乎要求的分数,所以就将A[p]/A[q-1]也加入优先队列中。
在实现中,为了保证最小的值首先被从pq中取出,我们将分数取负作为优先队列中的key。算法的空间复杂度为O(n),时间复杂度为O(Klogn)。
https://leetcode.com/problems/k-th-smallest-prime-fraction/discuss/116107/Java-Better-than-O(NlogN)-it-can-be-O(KlogK)
public int[] kthSmallestPrimeFraction(int[] A, int K) {
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> A[a[0]] * A[b[1]] - A[a[1]] * A[b[0]]);
pq.offer(new int[]{0, A.length - 1});
while (K > 1 && !pq.isEmpty()) {
int[] cur = pq.poll();
if (cur[1] == A.length - 1 && cur[0] + 1 < cur[1]) {
pq.offer(new int[]{cur[0] + 1, cur[1]});
}
if (cur[0] < cur[1] - 1) {
pq.offer(new int[]{cur[0], cur[1] - 1});
}
K--;
}
if (pq.isEmpty()) {
throw new RuntimeException("invalid input.");
}
return new int[]{A[pq.peek()[0]], A[pq.peek()[1]]};
}https://leetcode.com/problems/k-th-smallest-prime-fraction/discuss/115531/C%2B%2B-9lines-priority-queue
it is like find
k-th smallest element in n sorted array, which has a classic solution using priority_queue
consider an input of
https://leetcode.com/problems/k-th-smallest-prime-fraction/discuss/115486/Java-AC-O(max(nk)-*-logn)-Short-Easy-PriorityQueue[n1, n2, n3, n4, n5], the possible factors are:[n1/n5, n1/n4, n1/n3, n1/n2, n1/n1][n2/n5, n2/n4, n2/n3, n2/n2][n3/n5, n3/n4, n3/n3][n4/n5, n4/n4][n5/n5]http://bookshadow.com/weblog/2018/02/18/leetcode-k-th-smallest-prime-fraction/
This solution probably doesn't have the best runtime but it's really simple and easy to understand.
Says if the list is
[1, 7, 23, 29, 47], we can easily have this table of relationships1/47 < 1/29 < 1/23 < 1/7
7/47 < 7/29 < 7/23
23/47 < 23/29
29/47
So now the problem becomes "find the kth smallest element of (n-1) sorted list"
Following is my implementation using PriorityQueue, running time is O(nlogn) O(max(n,k) * logn), space is O(n)
public int[] kthSmallestPrimeFraction(int[] a, int k) {
int n = a.length;
// 0: numerator idx, 1: denominator idx
PriorityQueue<int[]> pq = new PriorityQueue<>(new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
int s1 = a[o1[0]] * a[o2[1]];
int s2 = a[o2[0]] * a[o1[1]];
return s1 - s2;
}
});
for (int i = 0; i < n-1; i++) {
pq.add(new int[]{i, n-1});
}
for (int i = 0; i < k-1; i++) {
int[] pop = pq.remove();
int ni = pop[0];
int di = pop[1];
if (pop[1] - 1 > pop[0]) {
pop[1]--;
pq.add(pop);
}
}
int[] peek = pq.peek();
return new int[]{a[peek[0]], a[peek[1]]};
}X. https://leetcode.com/problems/k-th-smallest-prime-fraction/discuss/115819/Summary-of-solutions-for-problems-%22reducible%22-to-LeetCode-378
SOLUTION THREE -- Using ZigzagSearch
- Time complexity:
O(n^2) - Space complexity:
O(1)
public int[] kthSmallestPrimeFraction(int[] A, int K) {
int n = A.length;
int row = 0;
int col = n - 1;
for (int cnt_le = 0, cnt_lt = 0; true; cnt_le = 0, cnt_lt = 0) {
for (int i = 0, j = n - 1, p = n - 1; i < n; i++) {
while (j >= 0 && A[i] * A[n - 1 - col] > A[n - 1 - j] * A[row]) j--;
cnt_le += (j + 1);
while (p >= 0 && A[i] * A[n - 1 - col] >= A[n - 1 - p] * A[row]) p--;
cnt_lt += (p + 1);
}
if (cnt_le < K) {
row++;
} else if (cnt_lt >= K) {
col--;
} else {
return new int[] {A[row], A[n - 1 - col]};
}
}
}
Remarks:
- We no longer need to keep track of the largest fraction in the matrix that is no greater than each candidate solution, because now all the candidate solutions are formed by integer pairs from the input array itself.
- The above solution can be further optimized due to the fact that there are no duplicates in the fraction matrix. This implies we always have
cnt_lt = cnt_le - 1, therefore the loop for conutingcnt_ltcan be dropped. You may refer to lixx2100's comment for more information.
X. https://blog.csdn.net/u014688145/article/details/79335163
二分,先找到这个第k小的数,接着再小范围暴力搜索,居然能过。
public int[] kthSmallestPrimeFraction(int[] a, int K) {
double low = 0, high = 1;
double eps = 1e-8;
int n = a.length;
for (int rep = 0; rep < 50; ++rep) {
double x = low + (high - low) / 2;
int num = 0;
for (int i = 0; i < n; i++) {
int ind = Arrays.binarySearch(a, (int) (x * a[i]));
if (ind < 0)
ind = -ind - 2;
num += ind + 1;
}
if (num >= K) {
high = x;
} else {
low = x;
}
}
for (int i = 0; i < n; ++i) {
double find = a[i] * high;
int idx = Arrays.binarySearch(a, (int) find);
if (idx < 0)
idx = -idx;
for (int j = -1; j <= 1; ++j) {
if (j + idx >= 0 && j + idx < n && Math.abs(a[j + idx] - find) < eps) {
return new int[] { a[j + idx], a[i] };
}
}
}
return new int[] { -1, -1 };
}
https://leetcode.com/problems/k-th-smallest-prime-fraction/discuss/115819/Summary-of-solutions-for-problems-%22reducible%22-to-LeetCode-378
SOLUTION THREE -- Using ZigzagSearch
- Time complexity:
O(n^2) - Space complexity:
O(1)
public int[] kthSmallestPrimeFraction(int[] A, int K) {
int n = A.length;
int row = 0;
int col = n - 1;
for (int cnt_le = 0, cnt_lt = 0; true; cnt_le = 0, cnt_lt = 0) {
for (int i = 0, j = n - 1, p = n - 1; i < n; i++) {
while (j >= 0 && A[i] * A[n - 1 - col] > A[n - 1 - j] * A[row]) j--;
cnt_le += (j + 1);
while (p >= 0 && A[i] * A[n - 1 - col] >= A[n - 1 - p] * A[row]) p--;
cnt_lt += (p + 1);
}
if (cnt_le < K) {
row++;
} else if (cnt_lt >= K) {
col--;
} else {
return new int[] {A[row], A[n - 1 - col]};
}
}
}
Remarks:
- We no longer need to keep track of the largest fraction in the matrix that is no greater than each candidate solution, because now all the candidate solutions are formed by integer pairs from the input array itself.
- The above solution can be further optimized due to the fact that there are no duplicates in the fraction matrix. This implies we always have
cnt_lt = cnt_le - 1, therefore the loop for conutingcnt_ltcan be dropped. You may refer to lixx2100's comment for more information.
This is essentially a Young tableau. Now, given any fraction in the table, we can find its rank in
O(n) time. Using the rank function as a blackbox, we can then find the K-th smallest fractions in O(n^2) time.