https://leetcode.com/problems/bricks-falling-when-hit/
We have a grid of 1s and 0s; the 1s in a cell represent bricks. A brick will not drop if and only if it is directly connected to the top of the grid, or at least one of its (4-way) adjacent bricks will not drop.
We will do some erasures sequentially. Each time we want to do the erasure at the location (i, j), the brick (if it exists) on that location will disappear, and then some other bricks may drop because of that erasure.
Return an array representing the number of bricks that will drop after each erasure in sequence.
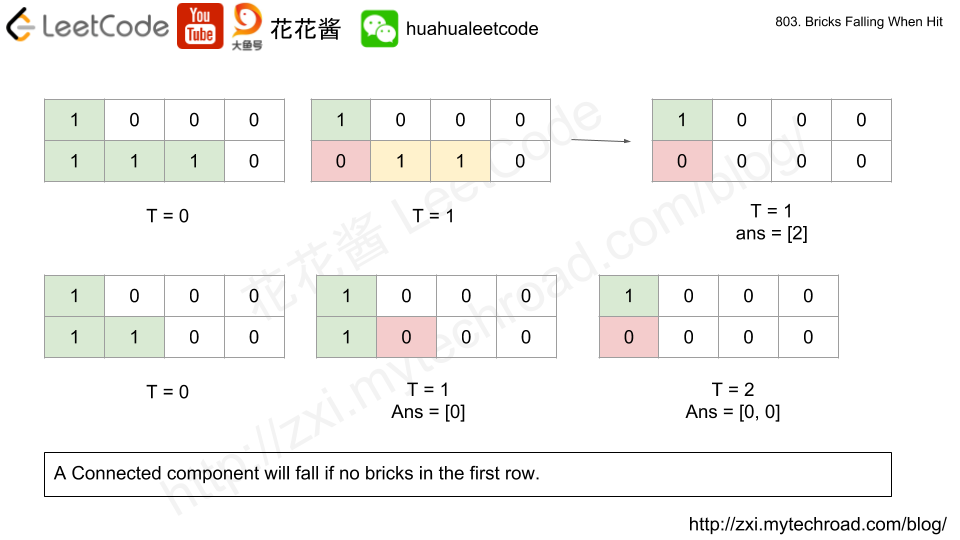
Example 1: Input: grid = [[1,0,0,0],[1,1,1,0]] hits = [[1,0]] Output: [2] Explanation: If we erase the brick at (1, 0), the brick at (1, 1) and (1, 2) will drop. So we should return 2.
Example 2: Input: grid = [[1,0,0,0],[1,1,0,0]] hits = [[1,1],[1,0]] Output: [0,0] Explanation: When we erase the brick at (1, 0), the brick at (1, 1) has already disappeared due to the last move. So each erasure will cause no bricks dropping. Note that the erased brick (1, 0) will not be counted as a dropped brick.
Note:
- The number of rows and columns in the grid will be in the range [1, 200].
- The number of erasures will not exceed the area of the grid.
- It is guaranteed that each erasure will be different from any other erasure, and located inside the grid.
- An erasure may refer to a location with no brick - if it does, no bricks drop
这道题给了我们一个由0和1组成的grid，说是1代表砖头，当砖头连着顶端的时候，就不会掉落，当某个砖头连着不会掉落的砖头时，其本身也不会掉落。然后我们要去掉一些砖头，当去掉某个砖头时，与其相连的砖头可能也会同时掉落。所以这里让我们求同时掉落的砖头个数。博主书读的不少，不会受骗，这尼玛不就是泡泡龙游戏么。其中泡泡龙的一大技巧就是挂葡萄，当关键节点处的泡泡被打掉后，这整个一串都可以直接掉下来。这里也是一样啊，grid的顶端就是游戏界面的顶端，然后砖头就是泡泡，去掉砖头就是消掉某个地方的泡泡，然后掉落的砖头就是掉下的泡泡啦。
看了discussion之后发现别人提出了很好的想法.
与其将砖头一块块按顺序敲碎，不如把砖头按相反的顺序一块块的加回来.
这样的好处是很好的解决了没敲碎一块砖头之后需要更新grid的操作!! (因为后面要敲的很可能在之前已经跟着落掉了)
而且这种方法也很好的解决了
de-union的问题. 把砖头加回来只需要union.
X. Union Find
http://hehejun.blogspot.com/2018/03/leetcodebricks-falling-when-hit.html
图的连接性的问题，很自然地会想到用并查集。这道题的问题是我们每次erase一个1，是相当于disconnect两个node，但是并查集只支持连接两个node，而不支持disconnect，所以这里我们要想办法把disconnect变成connect。如果我们按照从头到尾的顺序disconnect的话，我们反向connect就可以达到一样的效果。具体的做法是，把所有对于要抹去的brick先从grid当中消除，之后我们反向加入brick，然后看每次并查集中对应的component的size有没有变化。由于所有在顶端的点都是自动联通的，我们设定一个super node链接所有顶端的节点。假设grid有r行c列，hits长度为n，时间复杂度O((r * c + n) * lg*(r * c))，
http://hehejun.blogspot.com/2018/03/leetcodebricks-falling-when-hit.html
图的连接性的问题，很自然地会想到用并查集。这道题的问题是我们每次erase一个1，是相当于disconnect两个node，但是并查集只支持连接两个node，而不支持disconnect，所以这里我们要想办法把disconnect变成connect。如果我们按照从头到尾的顺序disconnect的话，我们反向connect就可以达到一样的效果。具体的做法是，把所有对于要抹去的brick先从grid当中消除，之后我们反向加入brick，然后看每次并查集中对应的component的size有没有变化。由于所有在顶端的点都是自动联通的，我们设定一个super node链接所有顶端的节点。假设grid有r行c列，hits长度为n，时间复杂度O((r * c + n) * lg*(r * c))，
主要思路是反向unionfind。
具体的做法是首先遍历一遍hits数组，把所有要打的砖块位置打掉（标记成2）， 然后对所有剩下的砖块做四个方向的union（上下左右），所有与上边界相邻的点都留下，统计一下剩下的个数，这个个数就是打掉所有砖块后一定会剩下的个数。 然后我们再倒序便利一遍hits数组，把后面要打的先复原回原来的board，对复原的点坐四个方向的union，这时候得到的size就是所有必须通过这块砖才能保证不掉的砖块数量，用这个数量减去原先计算的一定会剩下的个数再减去1（打掉的这块）就是这次打后剩下的数量。完成整个遍历就得到了result数组。
具体的做法是首先遍历一遍hits数组，把所有要打的砖块位置打掉（标记成2）， 然后对所有剩下的砖块做四个方向的union（上下左右），所有与上边界相邻的点都留下，统计一下剩下的个数，这个个数就是打掉所有砖块后一定会剩下的个数。 然后我们再倒序便利一遍hits数组，把后面要打的先复原回原来的board，对复原的点坐四个方向的union，这时候得到的size就是所有必须通过这块砖才能保证不掉的砖块数量，用这个数量减去原先计算的一定会剩下的个数再减去1（打掉的这块）就是这次打后剩下的数量。完成整个遍历就得到了result数组。
public int[] hitBricks(int[][] grid, int[][] hits) {
int m = grid.length;
int n = grid[0].length;
//这里的 + 1主要是多一个0来表示顶，所有的第一排的砖在unionfind的时候都会直接与这个0相连。
UnionFind uf = new UnionFind(m * n + 1);
//首先把所有要打的砖块标记为2.
for (int[]hit : hits) {
if (grid[hit[0]][hit[1]] == 1) {
grid[hit[0]][hit[1]] = 2;
}
}
//然后对打掉后的数组中的砖块进行四个方向的union
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
unionAround(i, j, grid, uf);
}
}
}
//这个count就是打完后一定会剩下的砖块数量.
int count = uf.size[uf.find(0)];
int[] res = new int[hits.length];
//反向遍历hits数组，一个一个复原回board
for (int i = hits.length - 1; i >= 0; i--) {
int[] hit = hits[i];
if (grid[hit[0]][hit[1]] == 2) {
// 对于需要复原的这个砖块做四个方向union，主要是为了得到有多少砖必须通过这块砖才能连接到顶部。
unionAround(hit[0], hit[1], grid, uf);
//由于是从后向前，做完要把这块砖重新标记回来
grid[hit[0]][hit[1]] = 1;
}
//newSize就是复原这块砖之后，有多少与顶部相连的砖块.
int newSize = uf.size[uf.find(0)];
// 打掉当前砖块会掉的数量就是 复原后的数量- 开始时的数量 - 1 （本身）
res[i] = (newSize - count > 0) ? newSize - count - 1 : 0;
//由于是从后向前，所以下次循环时，这个砖还没掉，更新count。
count = newSize;
}
return res;
}
private void unionAround(int x, int y, int[][] grid, UnionFind uf) {
int m = grid.length;
int n = grid[0].length;
int[] dx = new int[] {-1, 1, 0, 0};
int[] dy = new int[] {0, 0, -1, 1};
for (int i = 0; i < 4; i++) {
int nextX = x + dx[i];
int nextY = y + dy[i];
if (nextX < 0 || nextX >= m || nextY < 0 || nextY >= n) continue;
if (grid[nextX][nextY] == 1) {
uf.union(x * n + y + 1, nextX * n + nextY + 1);
}
}
//第一排的直接与顶相连。
if (x == 0) {
uf.union(x * n + y + 1, 0);
}
}
}
class UnionFind {
int[] id;
int[] size;
public UnionFind(int len) {
id = new int[len];
size = new int[len];
for (int i = 0; i < len; i++) {
id[i] = i;
size[i] = 1;
}
}
public int find(int toFind) {
while (id[toFind] != toFind) {
id[toFind] = id[id[toFind]];
toFind = id[toFind];
}
return toFind;
}
public void union(int a, int b) {
int rootA = find(a);
int rootB = find(b);
if (rootA != rootB) {
id[rootA] = rootB;
size[rootB] += size[rootA];
}
}
The problem is about knowing information about the connected components of a graph as we cut vertices. In particular, we'll like to know the size of the "roof" (component touching the top edge) between each cut. Here, a cut refers to the erasure of a vertex.
As we may know, a useful data structure for joining connected components is a disjoint set union structure. The key idea in this problem is that we can use this structure if we work in reverse: instead of looking at the graph as a series of sequential cuts, we'll look at the graph after all the cuts, and reverse each cut.
Algorithm
We'll modify our typical disjoint-set-union structure to include a
dsu.size operation, that tells us the size of this component. The way we do this is whenever we make a component point to a new parent, we'll also send it's size to that parent.
We'll also include
dsu.top, which tells us the size of the "roof", or the component connected to the top edge. We use an ephemeral "source" node with label R * C where all nodes on the top edge (with row number 0) are connected to the source node.- Time Complexity: , where is the number of grid squares, is the length of
hits, and is the Inverse-Ackermann function. - Space Complexity: .
public int[] hitBricks(int[][] grid, int[][] hits) {
int R = grid.length, C = grid[0].length;
int[] dr = { 1, 0, -1, 0 };
int[] dc = { 0, 1, 0, -1 };
int[][] A = new int[R][C];
for (int r = 0; r < R; ++r)
A[r] = grid[r].clone();
for (int[] hit : hits)
A[hit[0]][hit[1]] = 0;
DSU dsu = new DSU(R * C + 1);
for (int r = 0; r < R; ++r) {
for (int c = 0; c < C; ++c) {
if (A[r][c] == 1) {
int i = r * C + c;
if (r == 0)
dsu.union(i, R * C);
if (r > 0 && A[r - 1][c] == 1)
dsu.union(i, (r - 1) * C + c);
if (c > 0 && A[r][c - 1] == 1)
dsu.union(i, r * C + c - 1);
}
}
}
int t = hits.length;
int[] ans = new int[t--];
while (t >= 0) {
int r = hits[t][0];
int c = hits[t][1];
int preRoof = dsu.top();
if (grid[r][c] == 0) {
t--;
} else {
int i = r * C + c;
for (int k = 0; k < 4; ++k) {
int nr = r + dr[k];
int nc = c + dc[k];
if (0 <= nr && nr < R && 0 <= nc && nc < C && A[nr][nc] == 1)
dsu.union(i, nr * C + nc);
}
if (r == 0)
dsu.union(i, R * C);
A[r][c] = 1;
ans[t--] = Math.max(0, dsu.top() - preRoof - 1);
}
}
return ans;
}
}
class DSU {
int[] parent;
int[] rank;
int[] sz;
public DSU(int N) {
parent = new int[N];
for (int i = 0; i < N; ++i)
parent[i] = i;
rank = new int[N];
sz = new int[N];
Arrays.fill(sz, 1);
}
public int find(int x) {
if (parent[x] != x)
parent[x] = find(parent[x]);
return parent[x];
}
public void union(int x, int y) {
int xr = find(x), yr = find(y);
if (xr == yr)
return;
if (rank[xr] < rank[yr]) {
int tmp = yr;
yr = xr;
xr = tmp;
}
if (rank[xr] == rank[yr])
rank[xr]++;
parent[yr] = xr;
sz[xr] += sz[yr];
}
public int size(int x) {
return sz[find(x)];
}
public int top() {
return size(sz.length - 1) - 1;
}
}
http://reeestart.me/2018/04/22/LeetCode-803-Bricks-Falling-When-Hit/
https://zxi.mytechroad.com/blog/searching/leetcode-803-bricks-falling-when-hit/
https://leetcode.com/problems/bricks-falling-when-hit/discuss/141229/JAVA-Simple-DFS-16ms-reversely-add-bricks-back
http://morecoder.com/article/1160431.html
首先遍历hits数组去掉所有打掉的砖块，然后从第一行开始用DFS找出所有不会掉落的砖块放入notDrop集合中，然后倒序遍历hits，从被打掉的砖块开始调用DFS，如果这个砖块周围某个砖块存在于notDrop集合中，则说明该砖块与顶部相连，不会掉落，因此就可以对这个砖块的四周调用DFS，找出所有的联通块插入notDrop中，然后比较插入前后的差值，别忘了减去打掉的这一块砖头不算http://www.cnblogs.com/grandyang/p/9362777.html
X. Brute Force
https://leetcode.com/problems/bricks-falling-when-hit/discuss/120057/C%2B%2B-DFS-(similar-to-LC749)
"mark each connecting parts with a unique id in this run" -- This operation is so smart. With this operation, there is no need to reset the vst for each run!
https://xingxingpark.com/Leetcode-803-Bricks-Falling-When-Hit/
https://blog.csdn.net/brazy/article/details/79678332
typedef pair<int, int> P;
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};
int used[205][205];
int n, m;
vector<vector<int>> g;
int id;
vector<int> hitBricks(vector<vector<int>>& grid, vector<vector<int>>& hits) {
vector<int> res;
n = grid.size();
m = grid[0].size();
g.swap(grid);
id = 1;
for(int i = 0; i < hits.size(); ++i)
{
vector<int> pos = hits[i];
if(g[pos[0]][pos[1]] == 0)
{
res.push_back(0);
continue;
}
g[pos[0]][pos[1]] = 0;
int cnt = 0;
for(int j = 0; j < 4; ++j)
{
int nx = pos[0] + dx[j];
int ny = pos[1] + dy[j];
if(valid(nx, ny) && g[nx][ny] == 1 && dfs(nx, ny))
{
cnt += erase(nx, ny);
}
id += 1;
}
res.push_back(cnt);
}
return res;
}
bool valid(int x, int y)
{
return x >= 0 && x < n && y >= 0 && y < m;
}
bool dfs(int x, int y) //判断grid[x][y]是否掉落，true掉落，false不掉落
{
//if(used[x][y] == id) return true;
if(x == 0) return false;
used[x][y] = id;
for(int i = 0; i < 4; ++i)
{
int nx = x + dx[i];
int ny = y + dy[i];
if(valid(nx, ny) && g[nx][ny] == 1 && used[nx][ny] != id)
{
//used[x][y] = id;
if(!dfs(nx, ny)) return false;
}
}
return true;
}
int erase(int x, int y)
{
int res = 1;
g[x][y] = 0;
for(int i = 0; i < 4; ++i)
{
int nx = x + dx[i];
int ny = y + dy[i];
if(valid(nx, ny) && g[nx][ny] == 1)
{
res += erase(nx, ny);
}
}
return res;
}
TODO https://leetcode.com/problems/bricks-falling-when-hit/discuss/121072/Java-Solution
#Solution #1
理清思路之后很明显一看就是一道Union Find with dummy node的题目.
但是再仔细一想好像并没有这么简单, 比如最无脑的解法就是:
- 先构建一个Union Find
- 然后每次敲碎一块砖头之后更新Union Find
- 遍历一遍所有砖头看谁不再connect to top, 记录下来.
- 更新grid以及再次更新Union Find
先不提复杂度有多高, 看到
更新Union Find就知道这个解法不靠谱. 写了无数遍union find的代码至今没想过要怎么更新.
这个解法碰壁之后可能很容易会就此抛弃Union Find而改用DFS, 或者更准确的应该是
Flood Fill. 每次敲碎一块砖头之后, 利用Flood Fill找出所有还跟top连通的Components. 其余的都可以更新了. 这个解法是可行的, 但是复杂度会偏高: O(K * N), K is length of hits, N = m * n
看了discussion之后发现别人提出了很好的想法.
与其将砖头一块块按顺序敲碎，不如把砖头按相反的顺序一块块的加回来.
这样的好处是很好的解决了没敲碎一块砖头之后需要更新grid的操作!! (因为后面要敲的很可能在之前已经跟着落掉了)
而且这种方法也很好的解决了
de-union的问题. 把砖头加回来只需要union.
具体的步骤如下:
- 先把要敲掉的所有砖头都给敲了, mark成0
- 根据敲掉所有砖头之后的grid来构建Union Find
我们再来看一种使用并查集Union Find的方法来做的，接触过并查集题目的童鞋应该有印象，是专门处理群组问题的一种算法。最典型的就是岛屿问题(例如Number of Islands II)，很适合使用Union Find来做，LeetCode中有很多道可以使用这个方法来做的题，比如Friend Circles，Graph Valid Tree，Number of Connected Components in an Undirected Graph，和Redundant Connection等等。都是要用一个root数组，每个点开始初始化为不同的值，如果两个点属于相同的组，就将其中一个点的root值赋值为另一个点的位置，这样只要是相同组里的两点，通过find函数得到相同的值。当然初始化的时候也不用都赋为不同的值，如果表示的是坐标的话，我们也可以都初始化为-1，在find函数稍稍改动一下，也是可以的，这里就把判断 root[x] == x 改为 root[x] == -1 即可。这道题要稍稍复杂一些，我们不光需要并查集数组root，还需要知道每个位置右方和下方跟其相连的砖头个数数组count，还有标记每个位置是否相连且不会坠落的状态数组t，第一行各个位置的t值初始化为1。跟上面的方法类似，我们还是从最后一个砖头开始往回加，那么我们还是要把hits中所有的位置在grid中对应的值减1。然后我们要建立并查集的关系，我们遍历每一个位置，如果是砖头，那么我们对其右边和下边的位置进行检测，如果是砖头，我们就进行经典的并查集的操作，分别对当前位置和右边位置调用find函数，如果两个值不同，说明目前属于两个不同的群组，我们要链接上这两个位置，这里有个小问题需要注意一下，一般来说，我们链接群组的时候，root[x] = y 或 root[y] = x 都是可以的，但是这里我们需要使用第二种，为了跟后面的 count[x] += count[y] 对应起来，因为这里的y是在x的右边，所以count[x]要大于count[y]，这里x和y我们都使用x的群组号，这样能保证后面加到正确的相连的砖头个数。还有我们的t[x] 和 t[y] 也需要更新，因为两个位置要相连，所以只有其中有一方是跟顶端相连的，那么二者的t值都应该为1。初始化完成后，我们就从hits数组末尾开始往回加砖头，跟之前的方法一样，首先要判断之前是有砖头的，然后遍历周围四个新位置，如果位置合法且有砖头的话，再调用并查集的经典操作，对老位置和新位置分别调用find函数，如果不在同一个群组的话，我们需要一个变量cnt来记录可以掉落的砖头个数，如果新位置的t值为0，说明其除了当前位置之外不跟其他位置相连，我们将其count值加入cnt。然后就是链接两个群组，通知更新老位置的count值，新老位置的t值等等。当周围位置遍历完成后，如果当前位置的t值为1，则将cnt值存入结果res的对应位置
X. DFS
- For each day, hit and clear the specified brick.
- Find all connected components (CCs) using DFS.
- For each CC, if there is no brick that is on the first row that the entire cc will drop. Clear those CCs.
int[] dirs = new int[]{0, -1, 0, 1, 0};
int m;
int n;
int[][] g;
int seq;
int count;
public int[] hitBricks(int[][] grid, int[][] hits) {
this.g = grid;
this.m = grid.length;
this.n = grid[0].length;
int[] ans = new int[hits.length];
for (int i = 0; i < hits.length; ++i)
ans[i] = hit(hits[i][1], hits[i][0]);
return ans;
}
private int hit(int x, int y) {
if (x < 0 || x >= n || y < 0 || y >= m || g[y][x] == 0) return 0;
g[y][x] = 0;
int ans = 0;
for (int i = 0; i < 4; ++i) {
++seq;
count = 0;
if (!fall(x + dirs[i], y + dirs[i + 1], false)) continue;
ans += count;
++seq;
fall(x + dirs[i], y + dirs[i + 1], true);
}
return ans;
}
private boolean fall(int x, int y, boolean clear) {
if (x < 0 || x >= n || y < 0 || y >= m) return true;
if (g[y][x] == seq || g[y][x] == 0) return true;
if (y == 0) return false;
g[y][x] = clear ? 0 : seq;
++count;
for (int i = 0; i < 4; ++i)
if (!fall(x + dirs[i], y + dirs[i + 1], clear)) return false;
return true;
}
X. DFS reversely
理清思路之后很明显一看就是一道Union Find with dummy node的题目.
但是再仔细一想好像并没有这么简单, 比如最无脑的解法就是:
- 先构建一个Union Find
- 然后每次敲碎一块砖头之后更新Union Find
- 遍历一遍所有砖头看谁不再connect to top, 记录下来.
- 更新grid以及再次更新Union Find
先不提复杂度有多高, 看到
更新Union Find就知道这个解法不靠谱. 写了无数遍union find的代码至今没想过要怎么更新.
这个解法碰壁之后可能很容易会就此抛弃Union Find而改用DFS, 或者更准确的应该是
Flood Fill. 每次敲碎一块砖头之后, 利用Flood Fill找出所有还跟top连通的Components. 其余的都可以更新了. 这个解法是可行的, 但是复杂度会偏高: O(K * N), K is length of hits, N = m * n- Remove all bricks in hits. If the cell is originly 1, we set it to -1 so that we can add the brick back;
- DFS from the first row (roof), set all cells of bricks to 2 so that we know these cells have been visited.
- Iterate from the last hit to the first one, i.e., put the erasured bricks back. For every step:
3.1 if the cell is 0, continue;
3.2 else the cell is -1. Check if the cell is attathed to the roof (or any cell with value 2)
If no, continue;
Else, reuse the dfs function to count all the connected bricks (cells with value 1). These are bricks that fell down when we erase the hit! Remember to minus 1, which is the brick we erased.
首先遍历hits数组去掉所有打掉的砖块，然后从第一行开始用DFS找出所有不会掉落的砖块放入notDrop集合中，然后倒序遍历hits，从被打掉的砖块开始调用DFS，如果这个砖块周围某个砖块存在于notDrop集合中，则说明该砖块与顶部相连，不会掉落，因此就可以对这个砖块的四周调用DFS，找出所有的联通块插入notDrop中，然后比较插入前后的差值，别忘了减去打掉的这一块砖头不算http://www.cnblogs.com/grandyang/p/9362777.html
首先我们来想，我们肯定要统计出当前没有掉落的砖头数量，当去掉某个砖头后，我们可以统计当前还连着的砖头数量，二者做差值就是掉落的砖头数量。那么如何来统计不会掉落的砖头数量呢，由于顶层的砖头时不会掉落的，那么跟顶层相连的所有砖头肯定也不会掉落，我们就可以使用DFS来遍历，我们可以把不会掉落的砖头位置存入一个HashSet中，这样通过比较不同状态下HashSet中元素的个数，我们就知道掉落了多少砖头。然后我们再来想一个问题，在没有去除任何砖头的时候，我们DFS查找会遍历所有的砖头，当某个砖头去除后，可能没有连带其他的砖头，那么如果我们再来遍历一遍所有相连的砖头，相当于又把整个数组搜索了一遍，这样并不是很高效。我们可以试着换一个思路，如果我们先把要去掉的所有砖头都先去掉，这样我们遍历所有相连的砖头就是最终还剩下的砖头，然后我们从最后一个砖头开始往回加，每加一个砖头，我们就以这个砖头为起点，DFS遍历其周围相连的砖头，加入HashSet中，那么只会遍历那些会掉的砖头，那么增加的这些砖头就是会掉的砖头数量了，然后再不停的在增加前面的砖头，直到把hits中所有的砖头都添加回来了，那么我们也就计算出了每次会掉的砖头的个数。
好，我们使用一个HashSet来保存不会掉落的砖头，然后先遍历hits数组，把要掉落的砖头位置的值都减去一个1，这里有个需要注意的地方，hits里的掉落位置实际上在grid中不一定有砖头，就是说可能是本身为0的位置，那么我们减1后，数组中也可能会有-1，没有太大的影响，不过需要注意一下，这里不能使用 if (grid[i][j]) 来直接判断其是否为1，因为非0值-1也会返回true。然后我们对第一行的砖头都调用递归函数，因为顶端的砖头不会掉落，跟顶端的砖头相连的砖头也不会掉落，所以要遍历所有相连的砖头，将位置都存入noDrop。然后就是从最后一个位置往前加砖头，先记录noDrop当前的元素个数，然后grid中对应的值自增1，之后增加后的值为1了，才说明这块之前是有砖头的，然后我们看其上下左右位置，若有砖头，则对当前位置调用递归，还有一种情况是当前是顶层的话，还是要调用递归。递归调用完成后二者的差值再减去1就是掉落的砖头数，减1的原因是去掉的砖头不算掉落的砖头数中
vector<int> hitBricks(vector<vector<int>>& grid, vector<vector<int>>& hits) { int m = grid.size(), n = grid[0].size(), k = hits.size(); vector<int> res(k); unordered_set<int> noDrop; for (int i = 0; i < k; ++i) grid[hits[i][0]][hits[i][1]] -= 1; for (int i = 0; i < n; ++i) { if (grid[0][i] == 1) check(grid, 0, i, noDrop); } for (int i = k - 1; i >= 0; --i) { int oldSize = noDrop.size(), x = hits[i][0], y = hits[i][1]; if (++grid[x][y] != 1) continue; if ((x - 1 >= 0 && noDrop.count((x - 1) * n + y)) || (x + 1 < m && noDrop.count((x + 1) * n + y)) || (y - 1 >= 0 && noDrop.count(x * n + y - 1)) || (y + 1 < n && noDrop.count(x * n + y + 1)) || x == 0) { check(grid, x, y, noDrop); res[i] = noDrop.size() - oldSize - 1; } } return res; } void check(vector<vector<int>>& grid, int i, int j, unordered_set<int>& noDrop) { int m = grid.size(), n = grid[0].size(); if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] != 1 || noDrop.count(i * n + j)) return; noDrop.insert(i * n + j); check(grid, i - 1, j, noDrop); check(grid, i + 1, j, noDrop); check(grid, i, j - 1, noDrop); check(grid, i, j + 1, noDrop); }X.
1） 根据删除的brick 所在位置以及特性分为以下几种情况
#A, 当删除index处为0， 则drop为0.
#B, 当删除index处为1：
#B.1 当删除位置的brick 不和top相连， 则drop为0.
#B.2 当删除位置的brick 和 top 相连
#B.2.1 BFS 该brick四周的各个bricks，如果各个bricks 能够通过其他bricks 到达 top，则该子brick 不会drop
#B.2.2 否则会drop。
*/
public int[] hitBricks(int[][] grid, int[][] hits) {
if (hits.length == 0 || hits[0].length == 0) return null;
//删除 hits中所有的bricks， 进而为下面找出所有不通过 hits 就能够到达top 的bricks 做准备。
//在remove中， 如果hit[i][j]在grid中为0， 同样会--，则为-1.
removeHitBrick(grid, hits);
//标记所有剩余的bricks，如果该bricks 能够到达top，则设其为2.
markRemainBricks(grid);
//找出所有可能会drop的bricks
return searchFallingBrick(grid, hits);
}
private void removeHitBrick(int[][] grid, int[][] hits) {
for (int i = 0; i < hits.length; i++) {
//如果 hits处，没有brick 则设为-1，如果有brick 则清空为0
grid[hits[i][0]][hits[i][1]] = grid[hits[i][0]][hits[i][1]] - 1;
}
}
private void markRemainBricks(int[][] grid) {
for (int i = 0; i < grid[0].length; i++) {
//这里，只从第0行出发，dfs，找出所有能够到达top 的brick， 并将其设为2.
dfs(grid, 0, i);
}
}
private int[] searchFallingBrick(int[][] grid, int[][] hits) {
int[] result = new int[hits.length];
//从后向前遍历hits。
for (int i = hits.length - 1; i >= 0; i--) {
//如果grid 初为0，则表明hit处有brick。
if (grid[hits[i][0]][hits[i][1]] == 0) {
grid[hits[i][0]][hits[i][1]] = 1;
//如果hit处的brick能够到达top
if (isConnectToTop(grid, hits[i][0], hits[i][1])) {
//找出 删掉该brick 后， 有多少 其他的bricks 会掉落。
//因为从top出发能够到达的bricks 已经都设为2了，所以这些brick 不会再dfs中再次找到。
//同样的，当从hit处的brick出发，找到被影响的brick后，设这些brick为2，以便于后面的hit 不会重复计数。
result[i] = dfs(grid, hits[i][0], hits[i][1]) - 1;
} else {
//如果hit处的brick 无法到达top，则不会有任何brick 掉落。
result[i] = 0;
}
}
}
return result;
}
//判断从i,j出发，能否到达 top.
private boolean isConnectToTop(int[][] grid, int i, int j) {
if(i == 0) return true;
if (i - 1 >= 0 && grid[i - 1][j] == 2) {
return true;
}
if (i + 1 < grid.length && grid[i + 1][j] == 2) {
return true;
}
if (j - 1 >= 0 && grid[i][j - 1] == 2) {
return true;
}
if (j + 1 < grid[0].length && grid[i][j + 1] == 2) {
return true;
}
return false;
}
private int dfs(int[][] data, int row, int column) {
int arrayRow = data.length;
int arrayLine = data[0].length;
int effectBricks = 0;
if (row < 0 || row >= arrayRow) return effectBricks;
if (column < 0 || column >= arrayLine) return effectBricks;
if (data[row][column] == 1) {
data[row][column] = 2;
effectBricks = 1;
effectBricks += dfs(data, row + 1, column);
effectBricks += dfs(data, row - 1, column);
effectBricks += dfs(data, row, column + 1);
effectBricks += dfs(data, row, column - 1);
}
return effectBricks;
}
X. Brute Force
https://leetcode.com/problems/bricks-falling-when-hit/discuss/120057/C%2B%2B-DFS-(similar-to-LC749)
- when there is a hit, we change grid cell to 0.
- we assign all the resulting connecting parts a unique id and judge if it falls.
- for each falling parts, we count the number, reset the falling cell = 0.
- ++id (prepare to check another resulting parts of this run/start a new run of hit).
"mark each connecting parts with a unique id in this run" -- This operation is so smart. With this operation, there is no need to reset the vst for each run!
https://xingxingpark.com/Leetcode-803-Bricks-Falling-When-Hit/
每次落下一个砖块, 要从砖块的上下左右四个方向分别做
DFS, 第一遍判断DFS经过的砖块是否与顶部砖块连通, 如果不连通, 则该砖块会落下, 并且所有与之相连的砖块都不与顶部砖块连通, 因此做第二遍DFS, 标记访问过的砖块为落下. 注意每一次DFS都是一次新的遍历, 因此我们使用_id的来标记第_id次DFS, 并且在新的一次遍历前更新id.vector<vector<int>> _g; // 用一个私有变量 _g 可以减少 fall 函数的参数数量 int _m, _n; int _id = 1; vector<int> dx = {-1, 0, 0, 1}; vector<int> dy = {0, -1, 1, 0}; bool fall(int x, int y, bool isClear, int& cnt) { if (x < 0 || x >= _m || y < 0 || y >= _n) { return true; } if (_g[x][y] == _id || _g[x][y] == 0) { return true; } if (x == 0) { return false; } _g[x][y] = isClear ? 0 : _id; ++cnt; for (int i = 0; i < 4; ++i) { int xx = x + dx[i], yy = y + dy[i]; if (!fall(xx, yy, isClear, cnt)) { return false; } } return true; } public: vector<int> hitBricks(vector<vector<int>>& grid, vector<vector<int>>& hits) { _m = grid.size(); _n = grid[0].size(); _g.swap(grid); vector<int> rets; for (auto& hit : hits) { int ret = 0; int x = hit[0], y = hit[1]; _g[x][y] = 0; for (int i = 0; i < 4; ++i) { ++_id; int xx = x + dx[i]; int yy = y + dy[i]; int cnt = 0; if (!fall(xx, yy, false, cnt)) { continue; } ++_id; ret += cnt; fall(xx, yy, true, cnt); } rets.push_back(ret); } return rets; }
https://blog.csdn.net/brazy/article/details/79678332
typedef pair<int, int> P;
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};
int used[205][205];
int n, m;
vector<vector<int>> g;
int id;
vector<int> hitBricks(vector<vector<int>>& grid, vector<vector<int>>& hits) {
vector<int> res;
n = grid.size();
m = grid[0].size();
g.swap(grid);
id = 1;
for(int i = 0; i < hits.size(); ++i)
{
vector<int> pos = hits[i];
if(g[pos[0]][pos[1]] == 0)
{
res.push_back(0);
continue;
}
g[pos[0]][pos[1]] = 0;
int cnt = 0;
for(int j = 0; j < 4; ++j)
{
int nx = pos[0] + dx[j];
int ny = pos[1] + dy[j];
if(valid(nx, ny) && g[nx][ny] == 1 && dfs(nx, ny))
{
cnt += erase(nx, ny);
}
id += 1;
}
res.push_back(cnt);
}
return res;
}
bool valid(int x, int y)
{
return x >= 0 && x < n && y >= 0 && y < m;
}
bool dfs(int x, int y) //判断grid[x][y]是否掉落，true掉落，false不掉落
{
//if(used[x][y] == id) return true;
if(x == 0) return false;
used[x][y] = id;
for(int i = 0; i < 4; ++i)
{
int nx = x + dx[i];
int ny = y + dy[i];
if(valid(nx, ny) && g[nx][ny] == 1 && used[nx][ny] != id)
{
//used[x][y] = id;
if(!dfs(nx, ny)) return false;
}
}
return true;
}
int erase(int x, int y)
{
int res = 1;
g[x][y] = 0;
for(int i = 0; i < 4; ++i)
{
int nx = x + dx[i];
int ny = y + dy[i];
if(valid(nx, ny) && g[nx][ny] == 1)
{
res += erase(nx, ny);
}
}
return res;
}
TODO https://leetcode.com/problems/bricks-falling-when-hit/discuss/121072/Java-Solution
