Segment tree Part 2

Applications
https://cp-algorithms.com/data_structures/segment_tree.html

Finding the maximum and the number of times it appears

This task is very similar to the previous one. In addition of finding the maximum, we also have to find the number of occurrences of the maximum.

To solve this problem, we store a pair of numbers at each vertex in the tree: in addition to the maximum we also store the number of occurrences of it in the corresponding segment. Determining the correct pair to store at t[v]$t[v]$ can still be done in constant time using the information of the pairs stored at the child vertices. Combining two such pairs should be done in a separate function, since this will be a operation that we will do while building the tree, while answering maximum queries and while performing modifications.

Compute the greatest common divisor / least common multiple

In this problem we want to compute the GCD / LCM of all numbers of given ranges of the array.

This interesting variation of the Segment Tree can be solved in exactly the same way as the Segment Trees we derived for sum / minimum / maximum queries: it is enough to store the GCD / LCM of the corresponding vertex in each vertex of the tree. Combining two vertices can be done by computing the GCM / LCM of both vertices.

Counting the number of zeros, searching for the k$k$-th zero

In this problem we want to find the number of zeros in a given range, and additionally find the index of the k$k$-th zero using a second function.

Again we have to change the store values of the tree a bit: This time we will store the number of zeros in each segment in t[]$t[]$. It is pretty clear, how to implement the build$\text{build}$, update$\text{update}$ and count_zero$\text{count\_zero}$ functions, we can simple use the ideas from the sum query problem. Thus we solved the first part of the problem.

Now we learn how to solve the of problem of finding the k$k$-th zero in the array a[]$a[]$. To do this task, we will descend the Segment Tree, starting at the root vertex, and moving each time to either the left or the right child, depending on which segment contains the k$k$-th zero. In order to decide to which child we need to go, it is enough to look at the number of zeros appearing in the segment corresponding to the left vertex. If this precomputed count is greater or equal to k$k$, it is necessary to descend to the left child, and otherwise descent to the right child. Notice, if we chose the right child, we have to subtract the number of zeros of the left child from k$k$.

In the implementation we can handle the special case, a[]$a[]$ containing less than k$k$ zeros, by returning -1.

int find_kth(int v, int tl, int tr, int k) {
    if (k > t[v])
        return -1;
    if (tl == tr)
        return tl;
    int tm = (tl + tr) / 2;
    if (t[v*2] >= k)
        return find_kth(v*2, tl, tm, k);
    else 
        return find_kth(v*2+1, tm+1, tr, k - t[v*2]);
}

Saving the entire subarrays in each vertex

This is a separate subsection that stands apart from the others, because at each vertex of the Segment Tree we don't store information about the corresponding segment in compressed form (sum, minimum, maximum, ...), but store all element of the segment. Thus the root of the Segment Tree will store all elements of the array, the left child vertex will store the first half of the array, the right vertex the second half, and so on.

In its simplest application of this technique we store the elements in sorted order. In more complex versions the elements are not stored in lists, but more advanced data structures (sets, maps, ...). But all this methods have the common factor, that each vertex requires linear memory (i.e. proportional to the length of the corresponding segment).

The first natural question, when considering these Segment Trees, is about memory consumption. Intuitively this might look like O(n2)$O(n^2)$memory, but it turns out that the complete tree will only need O(nlogn)$O(n\log n)$ memory. Why is this so? Quite simply, because each element of the array falls into O(logn)$O(\log n)$ segments (remember the height of the tree is O(logn)$O(\log n)$).

So in spite of the apparent extravagance of such a Segment Tree, of consumes only slightly more memory than the usual Segment Tree.

Several typical applications of this data structure are described below. It is worth noting the similarity of these Segment Trees with 2D data structures (in fact this is a 2D data structure, but with rather limited capabilities).

https://www.geeksforgeeks.org/segment-tree-set-1-sum-of-given-range/

1. Leaf Nodes are the elements of the input array.
2. Each internal node represents some merging of the leaf nodes. The merging may be different for different problems. For this problem, merging is sum of leaves under a node.

An array representation of tree is used to represent Segment Trees. For each node at index i, the left child is at index 2*i+1, right child at 2*i+2 and the parent is at .

How does above segment tree look in memory?
Like Heap, segment tree is also represented as array. The difference here is, it is not a complete binary tree. It is rather a full binary tree (every node has 0 or 2 children) and all levels are filled except possibly the last level. Unlike Heap, the last level may have gaps between nodes. 

Below is memory representation of segment tree for input array {1, 3, 5, 7, 9, 11}
st[] = {36, 9, 27, 4, 5, 16, 11, 1, 3, DUMMY, DUMMY, 7, 9, DUMMY, DUMMY}

The dummy values are never accessed and have no use. This is some wastage of space due to simple array representation. We may optimize this wastage using some clever implementations, but code for sum and update becomes more complex.

Time Complexity for tree construction is O(n). There are total 2n-1 nodes, and value of every node is calculated only once in tree construction.

Time complexity to query is O(Logn). To query a sum, we process at most four nodes at every level and number of levels is O(Logn).

The time complexity of update is also O(Logn). To update a leaf value, we process one node at every level and number of levels is O(Logn).

Construction of Segment Tree from given array
We start with a segment arr[0 . . . n-1]. and every time we divide the current segment into two halves(if it has not yet become a segment of length 1), and then call the same procedure on both halves, and for each such segment, we store the sum in the corresponding node.
All levels of the constructed segment tree will be completely filled except the last level. Also, the tree will be a Full Binary Tree because we always divide segments in two halves at every level. Since the constructed tree is always a full binary tree with n leaves, there will be n-1 internal nodes. So total number of nodes will be 2*n – 1.
Height of the segment tree will be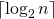 . Since the tree is represented using array and relation between parent and child indexes must be maintained, size of memory allocated for segment tree will be .

Query for Sum of given range
Once the tree is constructed, how to get the sum using the constructed segment tree. Following is the algorithm to get the sum of elements.

int getSum(node, l, r) 
{
   if the range of the node is within l and r
        return value in the node
   else if the range of the node is completely outside l and r
        return 0
   else
    return getSum(node's left child, l, r) + 
           getSum(node's right child, l, r)
}

Update a value
Like tree construction and query operations, the update can also be done recursively. We are given an index which needs to be updated. Let diff be the value to be added. We start from root of the segment tree and add diff to all nodes which have given index in their range. If a node doesn’t have given index in its range, we don’t make any changes to that node.

    int st[]; // The array that stores segment tree nodes

  

    /* Constructor to construct segment tree from given array. This

       constructor  allocates memory for segment tree and calls

       constructSTUtil() to  fill the allocated memory */

    SegmentTree(int arr[], int n)

    {

        // Allocate memory for segment tree

        //Height of segment tree

        int x = (int) (Math.ceil(Math.log(n) / Math.log(2)));

  

        //Maximum size of segment tree

        int max_size = 2 * (int) Math.pow(2, x) - 1;

  

        st = new int[max_size]; // Memory allocation

  

        constructSTUtil(arr, 0, n - 1, 0);

    }

  

    // A utility function to get the middle index from corner indexes.

    int getMid(int s, int e) {

        return s + (e - s) / 2;

    }

  

    /*  A recursive function to get the sum of values in given range

        of the array.  The following are parameters for this function.

  

      st    --> Pointer to segment tree

      si    --> Index of current node in the segment tree. Initially

                0 is passed as root is always at index 0

      ss & se  --> Starting and ending indexes of the segment represented

                    by current node, i.e., st[si]

      qs & qe  --> Starting and ending indexes of query range */

    int getSumUtil(int ss, int se, int qs, int qe, int si)

    {

        // If segment of this node is a part of given range, then return

        // the sum of the segment

        if (qs <= ss && qe >= se)

            return st[si];

  

        // If segment of this node is outside the given range

        if (se < qs || ss > qe)

            return 0;

  

        // If a part of this segment overlaps with the given range

        int mid = getMid(ss, se);

        return getSumUtil(ss, mid, qs, qe, 2 * si + 1) +

                getSumUtil(mid + 1, se, qs, qe, 2 * si + 2);

    }

  

    /* A recursive function to update the nodes which have the given 

       index in their range. The following are parameters

        st, si, ss and se are same as getSumUtil()

        i    --> index of the element to be updated. This index is in

                 input array.

       diff --> Value to be added to all nodes which have i in range */

    void updateValueUtil(int ss, int se, int i, int diff, int si)

    {

        // Base Case: If the input index lies outside the range of 

        // this segment

        if (i < ss || i > se)

            return;

  

        // If the input index is in range of this node, then update the

        // value of the node and its children

        st[si] = st[si] + diff;

        if (se != ss) {

            int mid = getMid(ss, se);

            updateValueUtil(ss, mid, i, diff, 2 * si + 1);

            updateValueUtil(mid + 1, se, i, diff, 2 * si + 2);

        }

    }

  

    // The function to update a value in input array and segment tree.

   // It uses updateValueUtil() to update the value in segment tree

    void updateValue(int arr[], int n, int i, int new_val)

    {

        // Check for erroneous input index

        if (i < 0 || i > n - 1) {

            System.out.println("Invalid Input");

            return;

        }

  

        // Get the difference between new value and old value

        int diff = new_val - arr[i];

  

        // Update the value in array

        arr[i] = new_val;

  

        // Update the values of nodes in segment tree

        updateValueUtil(0, n - 1, i, diff, 0);

    }

  

    // Return sum of elements in range from index qs (quey start) to

   // qe (query end).  It mainly uses getSumUtil()

    int getSum(int n, int qs, int qe)

    {

        // Check for erroneous input values

        if (qs < 0 || qe > n - 1 || qs > qe) {

            System.out.println("Invalid Input");

            return -1;

        }

        return getSumUtil(0, n - 1, qs, qe, 0);

    }

  

    // A recursive function that constructs Segment Tree for array[ss..se].

    // si is index of current node in segment tree st

    int constructSTUtil(int arr[], int ss, int se, int si)

    {

        // If there is one element in array, store it in current node of

        // segment tree and return

        if (ss == se) {

            st[si] = arr[ss];

            return arr[ss];

        }

  

        // If there are more than one elements, then recur for left and

        // right subtrees and store the sum of values in this node

        int mid = getMid(ss, se);

        st[si] = constructSTUtil(arr, ss, mid, si * 2 + 1) +

                 constructSTUtil(arr, mid + 1, se, si * 2 + 2);

        return st[si];

    }




https://www.geeksforgeeks.org/lazy-propagation-in-segment-tree/

In the previous post, update function was called to update only a single value in array. Please note that a single value update in array may cause multiple updates in Segment Tree as there may be many segment tree nodes that have a single array element in their ranges.

Below is simple logic used in previous post.
1) Start with root of segment tree.
2) If array index to be updated is not in current node’s range, then return
3) Else update current node and recur for children.

What if there are updates on a range of array indexes?
For example add 10 to all values at indexes from 2 to 7 in array. The above update has to be called for every index from 2 to 7. We can avoid multiple calls by writing a function updateRange() that updates nodes accordingly.

/* Function to update segment tree for range update in input     array.     si -> index of current node in segment tree     ss and se -> Starting and ending indexes of elements for                  which current nodes stores sum.     us and ue -> starting and ending indexes of update query     diff -> which we need to add in the range us to ue */ void updateRangeUtil(int si, int ss, int se, int us,                      int ue, int diff) {     // out of range     if (ss>se || ss>ue || se<us)         return ;        // Current node is a leaf node     if (ss==se)     {         // Add the difference to current node         tree[si] += diff;         return;     }        // If not a leaf node, recur for children.     int mid = (ss+se)/2;     updateRangeUtil(si*2+1, ss, mid, us, ue, diff);     updateRangeUtil(si*2+2, mid+1, se, us, ue, diff);        // Use the result of children calls to update this     // node     tree[si] = tree[si*2+1] + tree[si*2+2]; }