LeetCode 715 - Range Module

https://leetcode.com/problems/range-module/

A Range Module is a module that tracks ranges of numbers. Your task is to design and implement the following interfaces in an efficient manner.

addRange(int left, int right) Adds the half-open interval [left, right), tracking every real number in that interval. Adding an interval that partially overlaps with currently tracked numbers should add any numbers in the interval [left, right) that are not already tracked.

queryRange(int left, int right) Returns true if and only if every real number in the interval [left, right) is currently being tracked.

removeRange(int left, int right) Stops tracking every real number currently being tracked in the interval [left, right).

Example 1:

addRange(10, 20): null
removeRange(14, 16): null
queryRange(10, 14): true (Every number in [10, 14) is being tracked)
queryRange(13, 15): false (Numbers like 14, 14.03, 14.17 in [13, 15) are not being tracked)
queryRange(16, 17): true (The number 16 in [16, 17) is still being tracked, despite the remove operation)

Note:

A half open interval [left, right) denotes all real numbers left <= x < right.

0 < left < right < 10^9 in all calls to addRange, queryRange, removeRange.

The total number of calls to addRange in a single test case is at most 1000.

The total number of calls to queryRange in a single test case is at most 5000.

The total number of calls to removeRange in a single test case is at most 1000.

Approach #1: Maintain Sorted Disjoint Intervals [Accepted]

Because left, right < 10^9, we need to deal with the coordinates abstractly. Let's maintain some sorted structure of disjoint intervals. These intervals will be closed (eg. we don't store [[1, 2], [2, 3]]; we would store [[1, 3]]instead.)

We will maintain the structure as a TreeSet ranges = new TreeSet<Interval>();. We introduce a new Comparableclass Interval to represent our half-open intervals. They compare by right-most coordinate as later we will see that it simplifies our work. Also note that this ordering is consistent with equals, which is important when dealing with Sets.

Adding and Removing a Range

The basic structure of adding and removing a range is the same. First, we must iterate over the relevant subset of ranges. This is done using iterators so that we can itr.remove on the fly, and breaking when the intervals go too far to the right.

The critical logic of addRange is simply to make left, right the smallest and largest seen coordinates. After, we add one giant interval representing the union of all intervals seen that touched [left, right].

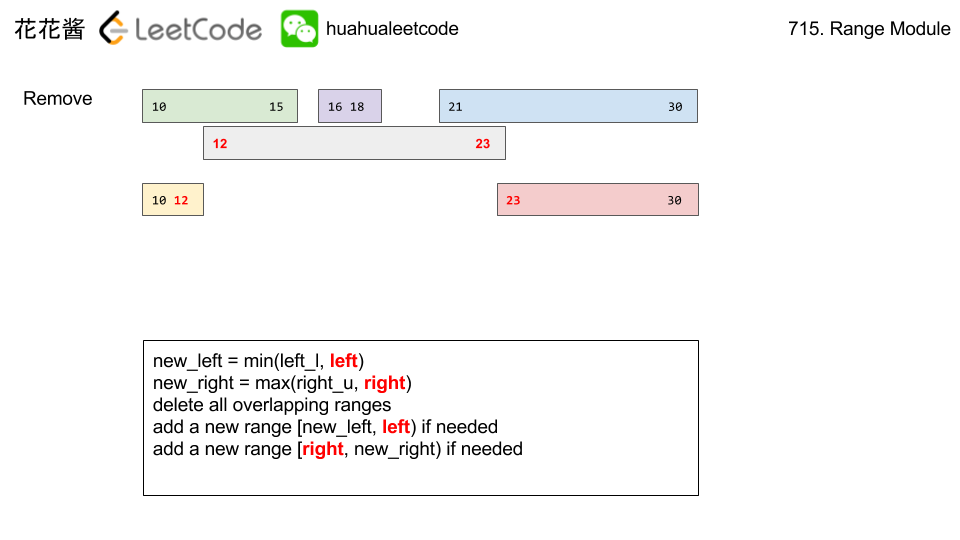
The logic of removeRange is to remember in todo the intervals we wanted to replace the removed interval with. After, we can add them all back in.

Querying a Range

As the intervals are sorted, we search to find the single interval that could intersect [left, right), then verify that it does. As the TreeSet uses a balanced (red-black) tree, this has logarithmic complexity.

• Time Complexity: Let $K$ be the number of elements in ranges. addRange and removeRange operations have $O(K)$ complexity. queryRange has $O(\log K)$ complexity. Because addRange, removeRange adds at most 1 interval at a time, you can bound these further. For example, if there are $A$ addRange, $R$ removeRange, and $Q$queryRange number of operations respectively, we can express our complexity as $O((A+R)^2 Q \log(A+R))$.
• Space Complexity: $O(A+R)$, the space used by ranges.

class RangeModule { TreeSet<Interval> ranges; public RangeModule() { ranges = new TreeSet(); } public void addRange(int left, int right) { Iterator<Interval> itr = ranges.tailSet(new Interval(0, left - 1)).iterator(); while (itr.hasNext()) { Interval iv = itr.next(); if (right < iv.left) break; left = Math.min(left, iv.left); right = Math.max(right, iv.right); itr.remove(); } ranges.add(new Interval(left, right)); } public boolean queryRange(int left, int right) { Interval iv = ranges.higher(new Interval(0, left)); return (iv != null && iv.left <= left && right <= iv.right); } public void removeRange(int left, int right) { Iterator<Interval> itr = ranges.tailSet(new Interval(0, left)).iterator(); ArrayList<Interval> todo = new ArrayList(); while (itr.hasNext()) { Interval iv = itr.next(); if (right < iv.left) break; if (iv.left < left) todo.add(new Interval(iv.left, left)); if (right < iv.right) todo.add(new Interval(right, iv.right)); itr.remove(); } for (Interval iv: todo) ranges.add(iv); } } class Interval implements Comparable<Interval>{ int left; int right; public Interval(int left, int right){ this.left = left; this.right = right; } public int compareTo(Interval that){ if (this.right == that.right) return this.left - that.left; return this.right - that.right; } }


X. https://leetcode.com/problems/range-module/discuss/108925/Java-Segment-Tree

X. TreeMap

http://www.cnblogs.com/grandyang/p/8586531.html

我们使用TreeMap来建立范围的起始位置和结束位置之间的映射，利用了TreeMap的自动排序功能，其会根据起始位置从小到大进行排序。既然是有序的，我们就可以利用二分法来快速进行查找了。

在加入范围函数中，我们首先用upper_bound函数来查找第一个大于left的位置，标记为l，再用upper_bound函数来查找第一个大于right的位置，标记为r。我们其实是想找第一个不大于left和right的位置的，由于C++没有floorKey这个函数，所以我们只能用upper_bound找大于left和right的位置，然后再往前移一个。如果l不是TreeMap中的第一个位置，且前面一个范围的结束位置小于left，说明和前一个范围没有交集，那么还是回到当前这个范围吧。如果此时l和r指向同一个位置，说明当前要加入的范围没有跟其他任何一个范围有交集，所以我们直接返回即可，不需要其他任何操作。否则的话我们将left和l指向范围的起始位置中的较小值赋给i，将right和r指向的前一个位置的结束位置的较大值赋给j，然后将l和r之间的范围都删除掉（注意这里r自增了1，是因为之前先自减了1），然后将i和j返回即可。返回后我们建立起这个映射即可。

在查找范围函数中，我们先用upper_bound找出第一个大于left位置的范围it，然后看如果it不是第一个范围，并且如果其前面的一个范围的结束位置大于等于right，说明已经完全包括这个要查找的范围，因为前一个范围的起始位置小于left，且结束位置大于等于right，直接返回true。

在删除范围函数中，查找重叠范围的方法跟加入范围函数中的操作一样，所以抽出来放到了find函数中，由于删除的范围有可能完全覆盖了原有范围，也有可能只是部分覆盖，将一个大的范围拆成了一个或者两个范围。所以我们判断，如果left大于覆盖范围的起始位置，那么将这段建立映射，同理，如果覆盖范围的结束位置大于right，同样建立这段的映射

X. https://blog.csdn.net/magicbean2/article/details/79327658
本题目可以用线段树来实现，但是这里我们用二分查找树来实现。我们定义一个map<int, int> invals，用来表示互不相交的线段，例如invales[left] = right就可以表示一个左闭右开的区间[left, right)。下面就看看各个函数分别怎么实现：
1）addRange(int left, int right)：首先找出[left, right)的前一个interval，然后判断我们是否需要在插入interval之前合并已有的interval，如果需要，则首先将待合并的interval删除，并更新left和right，最后将[left, right)插入二分查找树中。该函数的时间复杂度是O(nlogn)。

2）queryRange(int left, int right)：首先找出小于等于[left, right)的一个interval，然后判断它的右边是否覆盖掉了[left, right)，如果是，则返回false，否则说明该interval覆盖掉了[left, right)，所以返回true。该函数的时间复杂度仍然是O(nlogn)。

3）removeRange(int left, int right)：和addRange类似，我们首先找出和[left, right)重合的interval(s)，然后将该区间内的interval(s)都移除掉。但是需要注意的是，如果左边有残余的interval或者右边有残余的interval，则需要分别将它们保留。该函数的时间复杂度仍然是O(nlogn)。

整个算法的空间复杂度是O(n)。

https://leetcode.com/problems/range-module/discuss/108910/Java-TreeMap

TreeMap<Integer, Integer>, key is the starting index and value is the ending index of the interval.
Maintainence is done to make sure no overlap intervals exist in the Map.

    TreeMap<Integer, Integer> intervals = new TreeMap<>();
    
    public void addRange(int left, int right) {
        Integer start = intervals.floorKey(left);
        Integer end = intervals.floorKey(right);
        if(start != null && intervals.get(start) >= left){
            left = start;
        }
        if(end != null && intervals.get(end) > right){
            right = intervals.get(end);
        }
        intervals.put(left, right);
       
        intervals.subMap(left, false, right, true).clear();
    }
    
    public boolean queryRange(int left, int right) {
        Integer start = intervals.floorKey(left);
        if(start == null) return false;
        return intervals.get(start) >= right;
    }
    
    public void removeRange(int left, int right) {
        Integer start = intervals.floorKey(left);
        Integer end = intervals.floorKey(right);

        if(end != null && intervals.get(end) > right){
            intervals.put(right, intervals.get(end));
        }
        if(start != null && intervals.get(start) > left){
            intervals.put(start, left);
        }
        intervals.subMap(left, true, right, false).clear();
    }

X. http://www.cnblogs.com/grandyang/p/8586531.html
其实不管范围也好，区间也好，都是一回事，跟之前的区间的题目Insert Interval和Merge Intervals没有什么不同。这里的插入范围函数的实现方法跟之前那道Insert Interval的解法一样，直接抄过来就好。然后对于查找范围函数，由于题目中说只要有数字未被包括，就返回false。那么我们反过来想，只有当某个范围完全覆盖了这个要查找的范围才会返回true，所以我们可以遍历所有的范围，然后看是否有一个范围完全覆盖了要查找的范围，有的话返回true，循环结束后返回false。最后来看删除范围函数，其实现方法跟插入范围函数很类似，但又有少许不同。首先我们还是新建一个数组res存结果，然后遍历已有的范围，如果当前范围的结束位置小于等于要删除的范围的起始位置，由于题目中的范围定义是左开右闭，那么说明没有重叠，加入结果res，并且用变量cur自增1来记录当前位置。如果当前范围的起始位置大于等于要删除的范围的结束位置，说明咩有重叠，加入结果res。否则就是有重叠的情况，这里跟插入范围有所不同的是，插入范围只需要加入一个范围，而删除范围操作有可能将原来的大范围break成为两个小的范围，所以我们用一个临时数组t来存break掉后的小范围。如果当前范围的起始位置小于要删除的范围的起始位置left，说明此时一定有一段范围留下来了，即从当前范围的起始位置到要删除的范围的起始位置left，将这段范围加入临时数组t，同理，如果当前范围的结束位置大于要删除的范围的结束位置right，将这段范围加入临时数组t。最后将数组t加入结果res中的cur位置即可

    void addRange(int left, int right) {
        vector<pair<int, int>> res;
        int n = v.size(), cur = 0;
        for (int i = 0; i < n; ++i) {
            if (v[i].second < left) {
                res.push_back(v[i]);
                ++cur;
            } else if (v[i].first > right) {
                res.push_back(v[i]);
            } else {
                left = min(left, v[i].first);
                right = max(right, v[i].second);
            }
        }
        res.insert(res.begin() + cur, {left, right});
        v = res;
    }
    
    bool queryRange(int left, int right) {
        for (auto a : v) {
            if (a.first <= left && a.second >= right) return true;
        }
        return false;
    }
    
    void removeRange(int left, int right) {
        vector<pair<int, int>> res, t;
        int n = v.size(), cur = 0;
        for (int i = 0; i < n; ++i) {
            if (v[i].second <= left) {
                res.push_back(v[i]);
                ++cur;
            } else if (v[i].first >= right) {
                res.push_back(v[i]);
            } else {
                if (v[i].first < left) {
                    t.push_back({v[i].first, left});
                }
                if (v[i].second > right) {
                    t.push_back({right, v[i].second});
                }
            }
        }
        res.insert(res.begin() + cur, t.begin(), t.end());
        v = res;
    }

private:
    vector<pair<int, int>> v;

https://leetcode.com/problems/range-module/discuss/108912/C%2B%2B-vector-O(n)-and-map-O(logn)-compare-two-solutions

X. Videos
花花酱 LeetCode. 715 Range Module - 刷题找工作 EP96