https://codeforces.com/blog/entry/18169
https://web.stanford.edu/class/cs97si/04-dynamic-programming.pdf
◮ When working with subsets, it’s good to have a nice
representation of sets
◮ Idea: Use an integer to represent a set
– Concise representation of subsets of small integers {0, 1, . . .}
– If the ith (least significant) digit is 1, i is in the set
– If the ith digit is 0, i is not in the set
– e.g., 19 = 010011(2) in binary represent a set {0, 1, 4}
https://rameshaditya.wordpress.com/2017/10/06/dynamic-programming-sum-over-subset/
TODO https://github.com/cormacpayne/Data-Structures-and-Algorithms/blob/master/dynamic-programming/bitmask-dynamic-programming/bitmask-dynamic-programming.md
DP is a technique to avoid repetitive computing by using a memo to track the result of each subproblem. In some scenarios, the state of a subproblem can be represented as a bitmask, and then the memo becomes an array. For the properties of bitmask, it fits the problem whose subproblems are defined on the subsets of variables
https://medium.com/@sudsjaiswal/day-1-bit-masks-and-dp-monthofcode-6a0043d74549
https://codeforces.com/blog/entry/337
https://www.hackerearth.com/practice/algorithms/dynamic-programming/bit-masking/tutorial/
here number of set bits in .
This is just one problem that can be solved using DP+bitmasking. There's a whole lot.
Let's go to another problem, suppose we are given a graph and we want to find out if it contains a Hamiltonian Path. This problem can also be solved using DP+bitmasking in time complexity and space complexity. Here's a link to it's solution.
Iterating Over All Subsets of a Set
A subset of a set is a set that contains all or some of the elements of that set. For example if the set is {3, 5, 7} then some of its subsets are {} - the empty set, {3, 7}, {5, 7}, {5} and {3, 5, 7} - the original set. Often we need to find a subset with a particular property. If the original set is small, ie. has a small number of elements then it is sufficient to generate and test all its subsets. If the original set has n elements then it will contain 2^n subsets. Assuming that the computation required for each subset is small, we can usually do this for n up to 20.
Let us represent a subset with a unique binary number i. This way there will be a total of 2^n such unique numbers. The k-th element of the set can be either included or not included in the subset. We can associate the inclusion of the k-th element with a value of 1 at the k-th bit of i, similarly if the k-th bit is 0 then the k-th element is not included. For example, here is how we can associate a unique binary number from 0 to 7 with every subset of {3, 5, 7}:
Now all that remains is to iterate over all the subsets. Since these are just binary numbers, it suffices to iterate from 0 to 2^n-1 inclusive. In the following Java example we iterate over all the subsets of the set {"appple", "banana", "carrot"}. After generating a subset we can perform any action. Here for simplicity we print it. Notice that the 0-th subset is the empty subset, as it contains no elements.
The above procedure is very useful as it can be applied to many problems. One simple extension is to only generate subsets with no more than m elements. To achieve this we can modify the i-loop so that it only iterates over i that do not have more than m bits set to 1:
Let us decipher i=Integer.bitCount(i) < m ? i+1 : (i|(i-1))+1. We know that i+1 can only add at most one extra bit to i. So if the number of bits in i is less than m, then i+1 will not have more than m bits. Otherwise if the number of bits in i is m, we set i to (i|(i-1))+1. This value is i plus its lowest bit, ie it is the smallest integer greater than i whose bit count is no more than i's bit count. Since i starts with 0, we can see that this approach can never lead to i that has more than m bits. Warning: this does not work for m=0.
Another trick is to iterate over all the subsets of a subset in O(3^n) time:
Warning: i=0 (empty subset) is a special case and must be treated separately.
Finally, there are many other operations that can be performed on sets: union, intersection, subtraction, element addition, element deletion. All of these can be done with simple and extremely fast bitwise operations. If A and B are two sets whose bit-masks are a and b respectively then we have the following:
Union of A and B: a|b
Intersection of A and B: a&b
A "minus" B: a&(~b). This is a set of elements in A that are not in B.
Add k-th element to set A: a |= 1 << k
Delete k-th element of set A: a &= ~(1 << k)
For an excellent description of bitwise operations take a look at bmerry’s recipe.
https://apps.topcoder.com/forums/?module=Thread&threadID=671561&start=0
Problem: There are many ways to represent a subset of a set, but most of them are slow. This recipe shows how subsets from a domain of up to 64 elements can be very efficiently represented and manipulated as integers.
Solution: Consider a subset of the set {0, 1, ..., N - 1}. This can be represented by an N-bit binary number, where bit i (representing 2i) is 1 if element i is present, and 0 if element i is absent. Most modern languages support integers of up to 64 bits, allowing subsets of 64-element sets to be encoded (some languages also allow for arbitrary numbers of bits). In code examples, it is assumed that a 32-bit integer is being used.
TODO https://codeforces.com/blog/entry/45223
I am going to share my little knowledge on how to solve some problems involving calculation of Sum over Subsets(SOS)using dynamic programming. Thus the name SOS DP
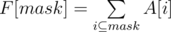
Bruteforce
3. Add the jth object to the subset (set the jth bit from 0 to 1):
use the bitwise OR operation A |= (1 << j).
4. Remove the jth object from the subset (set the jth bit from 1 to 0):
use the bitwise AND operation A &= ∼(1 << j).
5. Check whether the jth object is in the subset (check whether jth bit is 1): use the bitwise AND operation T = A & (1 << j). If T = 0, then the j-th item of the set is off. If T != 0 (to be precise, T = (1 << j)), then the j-th item of the set is on.
6. To toggle (flip the status of) the j-th item of the set: use the bitwise XOR operation A ∧ = (1 << j).
7. To get the value of the least significant bit that is on (first from the right): use T = (A & (-A)).
8. To turn on all bits in a set of size n: (be careful with overflows)
use A = (1 << n) - 1 ;
9. Iterate through all subsets of a set of size n:
for ( x = 0; x < (1 << n); ++x )
10. Iterate through all subsets of a subset y (not including empty set):
for ( x = y; x > 0; x = ( y & (x-1) ) )
Example of a subset problem: given a set of numbers, we want to find the sum of all subsets.
Sol: This is easy to code using bitmasks. we can use an array to store all the results.
int sum_of_all_subset ( vector< int > s ){
int n = s.size() ;
int results[ ( 1 << n ) ] ; // ( 1 << n )= 2^n
//initialize results to 0
memset( results, 0, sizeof( results ) ) ;
// iterate through all subsets
for( int i = 0 ; i < ( 1 << n ) ; ++ i ) { // for each subset, O(2^n)
for ( int j = 0; j < n ; ++ j ) { // check membership, O(n)
i f ( ( i & ( 1 << j ) ) ! = 0 ) // test if bit ‘j’ is turned on in subset ‘i’?
results[i] += s [j] ; // if yes, process ‘j’
}
}
}
11. LIMITATIONS:
a. Always check the size of the set to determine whether to use an int or long long or not using bitmask at all
b. Always use parenthesis to indicate the precedence of operations when doing bitwise operations!
When it involves bitwise operators and not putting parenthesis can yield undesirable results!
For example, let x = 5. Then x - 1 << 2 = 16, but x - (1 << 2) = 1
◮ When working with subsets, it’s good to have a nice
representation of sets
◮ Idea: Use an integer to represent a set
– Concise representation of subsets of small integers {0, 1, . . .}
– If the ith (least significant) digit is 1, i is in the set
– If the ith digit is 0, i is not in the set
– e.g., 19 = 010011(2) in binary represent a set {0, 1, 4}
https://rameshaditya.wordpress.com/2017/10/06/dynamic-programming-sum-over-subset/
TODO https://github.com/cormacpayne/Data-Structures-and-Algorithms/blob/master/dynamic-programming/bitmask-dynamic-programming/bitmask-dynamic-programming.md
Bitmask DP is a type of dynamic programming that uses bitmasks, in order to keep track of our current state in a problem.
A bitmask is nothing more than a number that defines which bits are on and off, or a binary string representation of the number.
http://my-zhang.github.io/blog/2014/04/20/dynamic-programming-with-bitmask/DP is a technique to avoid repetitive computing by using a memo to track the result of each subproblem. In some scenarios, the state of a subproblem can be represented as a bitmask, and then the memo becomes an array. For the properties of bitmask, it fits the problem whose subproblems are defined on the subsets of variables
https://medium.com/@sudsjaiswal/day-1-bit-masks-and-dp-monthofcode-6a0043d74549
This is a good first tutorial to learn about bit masks, it discusses the example given above and another problem called the Assignment problem. Here we get to use Dynamic Programming with Bit Masks to get a O(n*2^n) from a naive recursive solution of O(N!).
https://www.geeksforgeeks.org/bitmasking-and-dynamic-programming-set-1-count-ways-to-assign-unique-cap-to-every-person/
What is Bitmasking?
Suppose we have a collection of elements which are numbered from 1 to N. If we want to represent a subset of this set then it can be encoded by a sequence of N bits (we usually call this sequence a “mask”). In our chosen subset the i-th element belongs to it if and only if the i-th bit of the mask is set i.e., it equals to 1. For example, the mask 10000101 means that the subset of the set [1… 8] consists of elements 1, 3 and 8. We know that for a set of N elements there are total 2N subsets thus 2N masks are possible, one representing each subset. Each mask is, in fact, an integer number written in binary notation.
Suppose we have a collection of elements which are numbered from 1 to N. If we want to represent a subset of this set then it can be encoded by a sequence of N bits (we usually call this sequence a “mask”). In our chosen subset the i-th element belongs to it if and only if the i-th bit of the mask is set i.e., it equals to 1. For example, the mask 10000101 means that the subset of the set [1… 8] consists of elements 1, 3 and 8. We know that for a set of N elements there are total 2N subsets thus 2N masks are possible, one representing each subset. Each mask is, in fact, an integer number written in binary notation.
Our main methodology is to assign a value to each mask (and, therefore, to each subset) and thus calculate the values for new masks using values of the already computed masks. Usually our main target is to calculate value/solution for the complete set i.e., for mask 11111111. Normally, to find the value for a subset X we remove an element in every possible way and use values for obtained subsets X’1, X’2… ,X’k to compute the value/solution for X. This means that the values for X’i must have been computed already, so we need to establish an ordering in which masks will be considered. It’s easy to see that the natural ordering will do: go over masks in increasing order of corresponding numbers. Also, We sometimes, start with the empty subset X and we add elements in every possible way and use the values of obtained subsets X’1, X’2… ,X’k to compute the value/solution for X.
https://codeforces.com/blog/entry/337
https://www.hackerearth.com/practice/algorithms/dynamic-programming/bit-masking/tutorial/
First thing to make sure before using bitmasks for solving a problem is that it must be having small constraints, as solutions which use bitmasking generally take up exponential time and memory.
Let's first try to understand what Bitmask means. Mask in Bitmask means hiding something. Bitmask is nothing but a binary number that represents something. Let's take an example. Consider the set
Let's take a problem, given a set, count how many subsets have sum of elements greater than or equal to a given value.
Algorithm is simple:
solve(set, set_size, val)
count = 0
for x = 0 to power(2, set_size)
sum = 0
for k = 0 to set_size
if kth bit is set in x
sum = sum + set[k]
if sum >= val
count = count + 1
return count
To iterate over all the subsets we are going to each number from 0 to 2set_size-1
The above problem simply uses bitmask and complexity is O(2nn).
The above problem simply uses bitmask and complexity is O(2nn).
Assignment Problem:
There are persons and tasks, each task is to be alloted to a single person. We are also given a matrix of size , where denotes, how much person is going to charge for task . Now we need to assign each task to a person in such a way that the total cost is minimum. Note that each task is to be alloted to a single person, and each person will be alloted only one task.
There are persons and tasks, each task is to be alloted to a single person. We are also given a matrix of size , where denotes, how much person is going to charge for task . Now we need to assign each task to a person in such a way that the total cost is minimum. Note that each task is to be alloted to a single person, and each person will be alloted only one task.
The brute force approach here is to try every possible assignment. Algorithm is given below:
assign(N, cost)
for i = 0 to N
assignment[i] = i //assigning task i to person i
res = INFINITY
for j = 0 to factorial(N)
total_cost = 0
for i = 0 to N
total_cost = total_cost + cost[i][assignment[i]]
res = min(res, total_cost)
generate_next_greater_permutation(assignment)
return res
Let's try to improve it using dynamic programming. Suppose the state of is , where represents that person to have been assigned a task, and is a binary number, whose bit represents if the task has been assigned or not.
Now, suppose, we have , we can assign a task to person , iff task is not yet assigned to any peron i.e. then, will be given as:
Now, suppose, we have , we can assign a task to person , iff task is not yet assigned to any peron i.e. then, will be given as:
One thing to note here is is always equal to the number set bits in , so we can remove that. So the dp state now is just , and if we have , then
assign(N, cost)
for i = 0 to power(2,N)
dp[i] = INFINITY
dp[0] = 0
for mask = 0 to power(2, N)
x = count_set_bits(mask)
for j = 0 to N
if jth bit is not set in i
dp[mask|(1<<j)] = min(dp[mask|(1<<j)], dp[mask]+cost[x][j])
return dp[power(2,N)-1] This is just one problem that can be solved using DP+bitmasking. There's a whole lot.
Let's go to another problem, suppose we are given a graph and we want to find out if it contains a Hamiltonian Path. This problem can also be solved using DP+bitmasking in time complexity and space complexity. Here's a link to it's solution.
A subset of a set is a set that contains all or some of the elements of that set. For example if the set is {3, 5, 7} then some of its subsets are {} - the empty set, {3, 7}, {5, 7}, {5} and {3, 5, 7} - the original set. Often we need to find a subset with a particular property. If the original set is small, ie. has a small number of elements then it is sufficient to generate and test all its subsets. If the original set has n elements then it will contain 2^n subsets. Assuming that the computation required for each subset is small, we can usually do this for n up to 20.
Let us represent a subset with a unique binary number i. This way there will be a total of 2^n such unique numbers. The k-th element of the set can be either included or not included in the subset. We can associate the inclusion of the k-th element with a value of 1 at the k-th bit of i, similarly if the k-th bit is 0 then the k-th element is not included. For example, here is how we can associate a unique binary number from 0 to 7 with every subset of {3, 5, 7}:
Binary Number Subset
000 {}
001 {7}
010 {5}
011 {5, 7}
100 {3}
101 {3, 7}
110 {3, 5}
111 {3, 5, 7}
Now all that remains is to iterate over all the subsets. Since these are just binary numbers, it suffices to iterate from 0 to 2^n-1 inclusive. In the following Java example we iterate over all the subsets of the set {"appple", "banana", "carrot"}. After generating a subset we can perform any action. Here for simplicity we print it. Notice that the 0-th subset is the empty subset, as it contains no elements.
String[] set={"apple", "banana", "carrot"}; int n=set.length; // iterate over all the subsets for (int i=0; i < (1<<n); i++) { // generate the i-th subset Vector subset=new Vector(); for (int k=0; k < n; k++) { if ((i&(1<<k)) > 0) subset.add(set[k]); } // perform an action over the subset, here just print it System.out.print("Subset "+i+":"); for (int k=0; k<subset.size(); k++) System.out.print(" "+subset.get(k)); System.out.println(); }
The above procedure is very useful as it can be applied to many problems. One simple extension is to only generate subsets with no more than m elements. To achieve this we can modify the i-loop so that it only iterates over i that do not have more than m bits set to 1:
// iterate over all the subsets with no more than m elements for (int i = 0; i < (1<<n); i=Integer.bitCount(i) < m ? i+1 : (i|(i-1))+1) { ... }
Let us decipher i=Integer.bitCount(i) < m ? i+1 : (i|(i-1))+1. We know that i+1 can only add at most one extra bit to i. So if the number of bits in i is less than m, then i+1 will not have more than m bits. Otherwise if the number of bits in i is m, we set i to (i|(i-1))+1. This value is i plus its lowest bit, ie it is the smallest integer greater than i whose bit count is no more than i's bit count. Since i starts with 0, we can see that this approach can never lead to i that has more than m bits. Warning: this does not work for m=0.
Another trick is to iterate over all the subsets of a subset in O(3^n) time:
// iterate over all the subsets for (int i=0; i < (1<<n); i++) { // iterate over all the subsets of the i-th subset for(int i2 = i; i2 > 0; i2 = (i2-1) & i) { // generate the subset induced by i2 ... } }
Warning: i=0 (empty subset) is a special case and must be treated separately.
Finally, there are many other operations that can be performed on sets: union, intersection, subtraction, element addition, element deletion. All of these can be done with simple and extremely fast bitwise operations. If A and B are two sets whose bit-masks are a and b respectively then we have the following:
Union of A and B: a|b
Intersection of A and B: a&b
A "minus" B: a&(~b). This is a set of elements in A that are not in B.
Add k-th element to set A: a |= 1 << k
Delete k-th element of set A: a &= ~(1 << k)
For an excellent description of bitwise operations take a look at bmerry’s recipe.
https://apps.topcoder.com/forums/?module=Thread&threadID=671561&start=0
Problem: There are many ways to represent a subset of a set, but most of them are slow. This recipe shows how subsets from a domain of up to 64 elements can be very efficiently represented and manipulated as integers.
Solution: Consider a subset of the set {0, 1, ..., N - 1}. This can be represented by an N-bit binary number, where bit i (representing 2i) is 1 if element i is present, and 0 if element i is absent. Most modern languages support integers of up to 64 bits, allowing subsets of 64-element sets to be encoded (some languages also allow for arbitrary numbers of bits). In code examples, it is assumed that a 32-bit integer is being used.
TODO https://codeforces.com/blog/entry/45223
I am going to share my little knowledge on how to solve some problems involving calculation of Sum over Subsets(SOS)using dynamic programming. Thus the name SOS DP
Given a fixed array A of 2N integers, we need to calculate ∀ x function F(x) = Sum of all A[i]such that x&i = i, i.e., i is a subset of x.
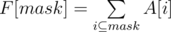
for(int mask = 0;mask < (1<<N); ++mask){
for(int i = 0;i < (1<<N); ++i){
if((mask&i) == i){
F[mask] += A[i];
}
}
}
This solution is quite straightforward and inefficient with time complexity of O(4N)
Suboptimal Solution
// iterate over all the masks
for (int mask = 0; mask < (1<<n); mask++){
F[mask] = A[0];
// iterate over all the subsets of the mask
for(int i = mask; i > 0; i = (i-1) & mask){
F[mask] += A[i];
}
}
Not as trivial, this solution is more efficient with time complexity of O(3N). To calculate the time complexity of this algorithm, notice that for each mask we iterate only over its subsets. Therefore if a mask has K on bits, we do 2K iterations. Also total number of masks with Kon bits is 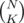 . Therefore total iterations =
. Therefore total iterations = 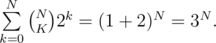
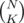 . Therefore total iterations =
. Therefore total iterations =