https://leetcode.com/problems/cat-and-mouse/
Approach 1: Minimax / Percolate from Resolved States
https://leetcode.com/problems/cat-and-mouse/discuss/181681/5ms-Java-solution-with-brief-comment
A game on an undirected graph is played by two players, Mouse and Cat, who alternate turns.
The graph is given as follows:
graph[a] is a list of all nodes b such that ab is an edge of the graph.
Mouse starts at node 1 and goes first, Cat starts at node 2 and goes second, and there is a Hole at node 0.
During each player's turn, they must travel along one edge of the graph that meets where they are. For example, if the Mouse is at node
1, it must travel to any node in graph[1].
Additionally, it is not allowed for the Cat to travel to the Hole (node 0.)
Then, the game can end in 3 ways:
- If ever the Cat occupies the same node as the Mouse, the Cat wins.
- If ever the Mouse reaches the Hole, the Mouse wins.
- If ever a position is repeated (ie. the players are in the same position as a previous turn, and it is the same player's turn to move), the game is a draw.
Given a
graph, and assuming both players play optimally, return 1 if the game is won by Mouse, 2 if the game is won by Cat, and 0 if the game is a draw.
Example 1:
Input: [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]] Output: 0 Explanation: 4---3---1 | | 2---5 \ / 0
Note:
3 <= graph.length <= 50- It is guaranteed that
graph[1]is non-empty. - It is guaranteed that
graph[2]contains a non-zero element.
The state of the game can be represented as
(m, c, t) where m is the location of the mouse, c is the location of the cat, and t is 1 if it is the mouse's move, else 2. Let's call these states nodes. These states form a directed graph: the player whose turn it is has various moves which can be considered as outgoing edges from this node to other nodes.
Some of these nodes are already resolved: if the mouse is at the hole
(m = 0), then the mouse wins; if the cat is where the mouse is (c = m), then the cat wins. Let's say that nodes will either be colored , , or depending on which player is assured victory.
As in a standard minimax algorithm, the Mouse player will prefer nodes first, nodes second, and nodes last, and the Cat player prefers these nodes in the opposite order.
Algorithm
We will color each
node marked according to the following rule. (We'll suppose the node has node.turn = Mouse: the other case is similar.)- ("Immediate coloring"): If there is a child that is colored , then this node will also be colored .
- ("Eventual coloring"): If all children are colored , then this node will also be colored .
We will repeatedly do this kind of coloring until no
node satisfies the above conditions. To perform this coloring efficiently, we will use a queue and perform a bottom-up percolation:- Enqueue any node initially colored (because the Mouse is at the Hole, or the Cat is at the Mouse.)
- For every
nodein the queue, for eachparentof thatnode:- Do an immediate coloring of
parentif you can. - If you can't, then decrement the side-count of the number of children marked . If it becomes zero, then do an "eventual coloring" of this parent.
- All
parentsthat were colored in this manner get enqueued to the queue.
Proof of Correctness
Our proof is similar to a proof that minimax works.
Say we cannot color any nodes any more, and say from any node colored or we need at most moves to win. If say, some node marked is actually a win for Mouse, it must have been with moves. Then, a path along optimal play (that tries to prolong the loss as long as possible) must arrive at a node colored (as eventually the Mouse reaches the Hole.) Thus, there must have been some transition along this path.
If this transition occurred at a
node with node.turn = Mouse, then it breaks our immediate coloring rule. If it occured with node.turn = Cat, and all children of node have color , then it breaks our eventual coloring rule. If some child has color , then it breaks our immediate coloring rule. Thus, in this case nodewill have some child with , which breaks our optimal play assumption, as moving to this child ends the game in moves, whereas moving to the colored neighbor ends the game in moves.- Time Complexity: , where is the number of nodes in the graph. There are states, and each state has an outdegree of , as there are at most different moves.
- Space Complexity: .
public int catMouseGame(int[][] graph) {
int N = graph.length;
final int DRAW = 0, MOUSE = 1, CAT = 2;
int[][][] color = new int[50][50][3];
int[][][] degree = new int[50][50][3];
// degree[node] : the number of neutral children of this node
for (int m = 0; m < N; ++m)
for (int c = 0; c < N; ++c) {
degree[m][c][1] = graph[m].length;
degree[m][c][2] = graph[c].length;
for (int x : graph[c])
if (x == 0) {
degree[m][c][2]--;
break;
}
}
// enqueued : all nodes that are colored
Queue<int[]> queue = new LinkedList();
for (int i = 0; i < N; ++i)
for (int t = 1; t <= 2; ++t) {
color[0][i][t] = MOUSE;
queue.add(new int[] { 0, i, t, MOUSE });
if (i > 0) {
color[i][i][t] = CAT;
queue.add(new int[] { i, i, t, CAT });
}
}
// percolate
while (!queue.isEmpty()) {
// for nodes that are colored :
int[] node = queue.remove();
int i = node[0], j = node[1], t = node[2], c = node[3];
// for every parent of this node i, j, t :
for (int[] parent : parents(graph, i, j, t)) {
int i2 = parent[0], j2 = parent[1], t2 = parent[2];
// if this parent is not colored :
if (color[i2][j2][t2] == DRAW) {
// if the parent can make a winning move (ie. mouse to MOUSE), do so
if (t2 == c) {
color[i2][j2][t2] = c;
queue.add(new int[] { i2, j2, t2, c });
} else {
// else, this parent has degree[parent]--, and enqueue
// if all children of this parent are colored as losing moves
degree[i2][j2][t2]--;
if (degree[i2][j2][t2] == 0) {
color[i2][j2][t2] = 3 - t2;
queue.add(new int[] { i2, j2, t2, 3 - t2 });
}
}
}
}
}
return color[1][2][1];
}
// What nodes could play their turn to
// arrive at node (m, c, t) ?
public List<int[]> parents(int[][] graph, int m, int c, int t) {
List<int[]> ans = new ArrayList();
if (t == 2) {
for (int m2 : graph[m])
ans.add(new int[] { m2, c, 3 - t });
} else {
for (int c2 : graph[c])
if (c2 > 0)
ans.add(new int[] { m, c2, 3 - t });
}
return ans;
}
https://leetcode.com/problems/cat-and-mouse/discuss/176177/Most-of-the-DFS-solutions-are-WRONG-check-this-case
https://leetcode.com/problems/cat-and-mouse/discuss/176268/Perfect-Wrong-DFSDP-code-explained-in-detail-(Revised)
Basically the DFS with memo solutions generate status nodes like
(cat, mouse, turn). Before DFS to next level, we mark current node to 0 which means Draw. However, there might be cycles in the status graph.
i.e, We mark current node to
Draw. Then we go into the cycle and mark all nodes in the cycle to Draw. However, the right answer to current node could be Cat or Mouse, this can only be figured out in the later DFS. But the nodes in the cycle have already been marked to Draw mistakenly.
Check this case:
[[6],[4],[9],[5],[1,5],[3,4,6],[0,5,10],[8,9,10],[7],[2,7],[6,7]]
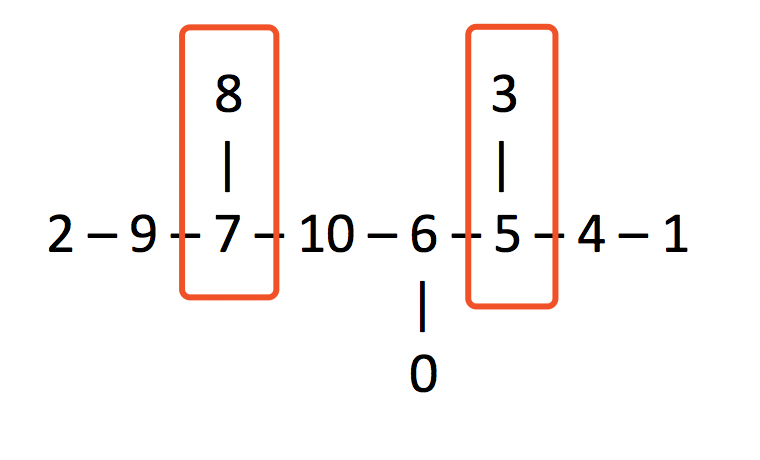
[[6],[4],[9],[5],[1,5],[3,4,6],[0,5,10],[8,9,10],[7],[2,7],[6,7]]

We will first get a
Draw in node (7, 5, mouse) then later we use this information to mark (9, 5, cat) to Draw. However (9, 5, cat) should be Mouse.
I believe the right solution should be using Topological traversal and coloring like the post in solution to solve the cycle problem. Also I noticed that many people used DP to solve this problem correctly but I don't understand those solutions. Can anyone help?
This test case was generated manually. Correct me if I'm wrong.
The idea of Topological traversal is start from each ending status, topologically traversal to color the previous status.
Similar to the solution, my code for reference:
public int catMouseGame(int[][] graph) {
int n = graph.length;
// (cat, mouse, mouseMove = 0)
int[][][] color = new int[n][n][2];
int[][][] outdegree = new int[n][n][2];
for (int i = 0; i < n; i++) { // cat
for (int j = 0; j < n; j++) { // mouse
outdegree[i][j][0] = graph[j].length;
outdegree[i][j][1] = graph[i].length;
for (int k : graph[i]) {
if (k == 0) {
outdegree[i][j][1]--;
break;
}
}
}
}
Queue<int[]> q = new LinkedList<>();
for (int k = 1; k < n; k++) {
for (int m = 0; m < 2; m++) {
color[k][0][m] = 1;
q.offer(new int[]{k, 0, m, 1});
color[k][k][m] = 2;
q.offer(new int[]{k, k, m, 2});
}
}
while (!q.isEmpty()) {
int[] cur = q.poll();
int cat = cur[0], mouse = cur[1], mouseMove = cur[2], c = cur[3];
if (cat == 2 && mouse == 1 && mouseMove == 0) {
return c;
}
int prevMouseMove = 1 - mouseMove;
for (int prev : graph[prevMouseMove == 1 ? cat : mouse]) {
int prevCat = prevMouseMove == 1 ? prev : cat;
int prevMouse = prevMouseMove == 1 ? mouse : prev;
if (prevCat == 0) {
continue;
}
if (color[prevCat][prevMouse][prevMouseMove] > 0) {
continue;
}
if (prevMouseMove == 1 && c == 2 || prevMouseMove == 0 && c == 1
|| --outdegree[prevCat][prevMouse][prevMouseMove] == 0) {
color[prevCat][prevMouse][prevMouseMove] = c;
q.offer(new int[]{prevCat, prevMouse, prevMouseMove, c});
}
}
}
return color[2][1][0];
}
https://leetcode.com/problems/cat-and-mouse/discuss/176268/Perfect-Wrong-DFSDP-code-explained-in-detail-(Revised)
Step 1 How to recognize a DP problem
Consider using DP whenever you have to make choices to arrive at the solution, specifically, when the solution relates to subproblems.
In <7 Steps to Solve any DP Interview Problem>, the second step is
Step 2 Identify problems variables
We come to identify a unique problem by defining three variable: when
cat_position is 2, mouse_position is 1, and it is the mouse's_turn to move, what is the answer to the current state (2, 1, True)?
We use
(cat, mouse, m_turn) to represent them.
The next step is:
step 3 Clearly express the recurrence relation
4---3---1
| |
2---5
\ /
0
Remember:
0 means a tie, 2 means the cat win, 1 means the mouse win.
Assume we know the answers to the states
(2, 3, False) is 0 (We don't care how do we know), thus we can know (2, 1, True) is 0, cause there is only one way from (2, 1, True) to its next move.
And by the same logic, if we want to know the answer to
(2, 3, False), which means the current cat position is 2, the current mouse position is 3, and it is the cat's turn to move, we need to know the answer to (4, 3, True), (5, 3, True). (In question, the cat cannot go to 0).
One question may occur to us: what's optimal in the context?
Ans: when it is the cat's turn to move, if the cat plays optimally (win
2 > draw 0 > lose 1),the cat will choose the next move state that returns 2 as long as there exists such one next move that returns 2(the cat wins). If not, he will the next move state that returns 0. Eventually, the cat will be faced with lose if all next moves that return 1.
Step 4: Identify the base cases
For the cat, the result will be 2 when the cat's next move position is the mouse's current position. Otherwise, the result come from its next move states.
For the mouse, the result will be 1 when the mouse's next move position is the hole
0. Otherwise, the result comes from its next move states.
Now we got the base cases. The next step is
Step 5: Decide if you want to implement it iteratively or recursively
Normally, recursive is more intuitive and easier to implement. For this problem, recursive way is easier to reason about, just as explained as above.
To make it more efficient, the next step is
To make it more efficient, the next step is
Step 6: Add memoization
Thus we don't have to calculate again when we encounter the same subproblems with memoization. Those repetitions very often lead to exponential time complexities.
The last step is
Step 7: Determine the time Complexity
Time Complexity: O(N^3), where N is the number of nodes in the graph. There are O(N^2) states, and each state has an outdegree of N, as there are at most N different moves.
Space Complexity: O(N^2). There are O(N^2) at most that we need to record.
Why it is wrong?
For example, if mouse is one step away from the hole, and dfs picks another root before the hole root, if that root is a loop and return to this node again, dfs would think that's a draw(return to previous state) instead of mouse win. —— Unicorn
def catMouseGame(self, graph):
"""
:type graph: List[List[int]]
:rtype: int
"""
n = len(graph)
state = [[-1]*n for _ in range(n)]
return self.search(state, graph, 1, 2)
def search(self, state, graph, m_pos, c_pos):
if state[m_pos][c_pos] != -1:
return state[m_pos][c_pos]
if m_pos == c_pos:
state[m_pos][c_pos] = 2
return 2
if m_pos == 0:
state[m_pos][c_pos] = 1
return 1
state[m_pos][c_pos] = 0
all_cat_win = True
for nxt_mouse in graph[m_pos]:
if nxt_mouse != c_pos:
all_mouse_win = True
exist_cat_win = False
for nxt_cat in graph[c_pos]:
if nxt_cat != 0:
nxt_state = self.search(state, graph, nxt_mouse, nxt_cat)
if nxt_state != 1:
all_mouse_win = False
if nxt_state == 2:
exist_cat_win = True
if not all_mouse_win and exist_cat_win:
break
if all_mouse_win:
state[m_pos][c_pos] = 1
return 1
if not exist_cat_win:
all_cat_win = False
state[m_pos][c_pos] = 2 if all_cat_win else 0
return state[m_pos][c_pos]
public int catMouseGame(int[][] graph) {
int size = graph.length;
int dp[][] = new int[size][size];
for (int i = 0; i < size; i++) Arrays.fill(dp[i], -1);
for (int i = 0; i < size; ++i) {
dp[0][i] = 1; // mouse reached home, m win
dp[i][i] = 2; // cat met mouse, cat win
}
return helper(graph, 1, 2, dp);
}
public int helper(int[][] graph, int mouse, int cat, int dp[][]) {
if (dp[mouse][cat] != -1) return dp[mouse][cat]; // use cached value
dp[mouse][cat] = 0; // if there is a cycle, draw
int mouseDefault = 2; // default cat win, try to update this number to 1 or 0
int[] mouseGoList = graph[mouse], catGoList = graph[cat];
for (int mouseGo : mouseGoList) {
if (mouseGo == cat) continue; // I'm a mouse, why go for a cat?
int catDefault = 1; // default mouse win, try to update this number to 2 or 0
for (int catGo : catGoList) {
if (catGo == 0) continue; // cannot go to hole
int next = helper(graph, mouseGo, catGo, dp);
if (next == 2) { // if cat win in this path, no need to continue
catDefault = 2;
break;
}
if (next == 0) { // at least it's a draw
catDefault = 0;
}
}
if (catDefault == 1) { // if mouse can win in this path, no need to continue
mouseDefault = 1;
break;
}
if (catDefault == 0) { // at least it's a draw
mouseDefault = 0;
}
}
dp[mouse][cat] = mouseDefault;
return dp[mouse][cat];
}