Related:
LeetCode 223 - Rectangle Area
LeetCode 850 - Rectangle Area II
LeetCode 939 - Minimum Area Rectangle
LeetCode 963 - Minimum Area Rectangle II
https://leetcode.com/problems/rectangle-area-ii/
https://www.hackerearth.com/practice/math/geometry/line-sweep-technique/tutorial/
The events for this problem are the vertical edges.When we encounter a left edge, we do some action and when we encounter a right edge, we do some other action.Left edge is represented by lower-left point and right edge by upper-right point
We start our algorithm by sorting the events by x coordinates. When a lower left point of a rectangle is hit (i.e., we encounter left edge of rectangle), we insert the rectangle into the set . When we hit an upper right point of a rectangle (we encounter right edge of rectangle), we remove the rectangle from the set. At any instance, the set contains only the rectangles which intersect the sweep line (rectangles whose left edges are visited but right edges are not).
The area swept at any instance is = y * x where y is the length of the sweep line which is actually cut by the rectangle(s) (sum of the vertical lengths of the orange region, in the figure below) and x is the distance between two events of this sweep line.
But here we just know which are the rectangles intersecting the sweep line. So, here we have a new problem: how to find the length of the sweep line cut by the rectangles?
The solution to this problem is pretty the same we have been doing by now. We use the line sweep technique to find this but this time we apply it 90 degrees rotated, i.e., we sweep a horizontal line from bottom to up . The events for this sweep line would be the horizontal edges of the active rectangles(rectangles cut by vertical sweep line). When we encounter a bottom horizontal edge of an active rectangle, we increment the counter (counter here maintains the number of rectangles that overlap at current time) and we decrement it on top horizontal edge of active rectangle. When the counter becomes zero from some non zero value, we have found cut length of the vertical sweep line, so we add the area to our final answer.
Let's see it running now:




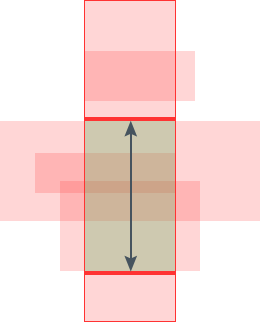
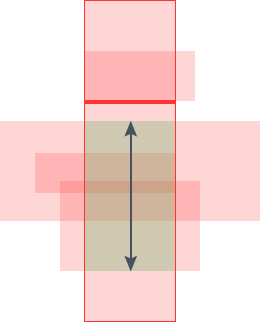
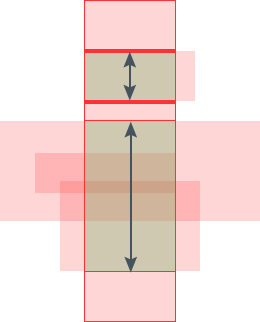
The images above show how we're doing the horizontal sweep bottom up. y is the sum of the length of the two arrows shown in the last image. This we do, for all events of vertical sweep line.
This was our algorithm. So, let's come to implementation part. For every event of vertical sweep line , we need to find the length of the cut on the sweep line, that means we need to go for horizontal sweep line. Here, we may use boolean array as our data structure because we would have once sorted the rectangles in order of vertical edges(vertical sweep) and once in order of horizontal edges(horizontal sweep), so we would have the sorting in both the directions.
The complexity of the algorithm can be easily seen to be . The complexity can be reduced by some other data structures such as BST instead of boolean array.
http://www.cnblogs.com/scau20110726/archive/2013/04/12/3016765.html

Approach #4: Segment Tree
Approach #3: Line Sweep
https://leetcode.com/problems/rectangle-area-ii/discuss/139835/TopJava-Solution-with-detailed-explaination-check-this-one-!
https://leetcode.com/problems/rectangle-area-ii/discuss/188832/Java-Line-Sweep-With-Sub-Class-Interval
X. https://www.hackerearth.com/practice/math/geometry/line-sweep-technique/practice-problems/algorithm/area-of-rectangles/editorial/
Approach #2: Coordinate Compression
思路是将坐标映射缩小范围,然后暴力标记,之后映射回去计算面积
Approach #1: Principle of Inclusion-Exclusion
https://www.cnblogs.com/sfzyk/p/9321181.html
https://www.gjxhlan.me/2018/06/10/leetcode-contest-88-solution/
https://blog.csdn.net/Bob__yuan/article/details/81394230
Find the total area covered by two rectilinear rectangles in a 2D plane.
Each rectangle is defined by its bottom left corner and top right corner as shown in the figure.
int computeArea(int A, int B, int C, int D, int E, int F, int G, int H)
{
int cross = 0; // 重叠区域
int top = min(D, H), bottom = max(B, F), left = max(A, E), right = min(C, G);
if(top > bottom && left < right)
cross = (top - bottom) * (right - left);
return (((C - A) * (D - B)) + ((G - E) * (H - F)) - cross);
}
LeetCode 223 - Rectangle Area
LeetCode 850 - Rectangle Area II
LeetCode 939 - Minimum Area Rectangle
LeetCode 963 - Minimum Area Rectangle II
https://leetcode.com/problems/rectangle-area-ii/
We are given a list of (axis-aligned)
rectangles. Each rectangle[i] = [x1, y1, x2, y2] , where (x1, y1) are the coordinates of the bottom-left corner, and (x2, y2) are the coordinates of the top-right corner of the ith rectangle.
Find the total area covered by all
rectangles in the plane. Since the answer may be too large, return it modulo 10^9 + 7.
Example 1:
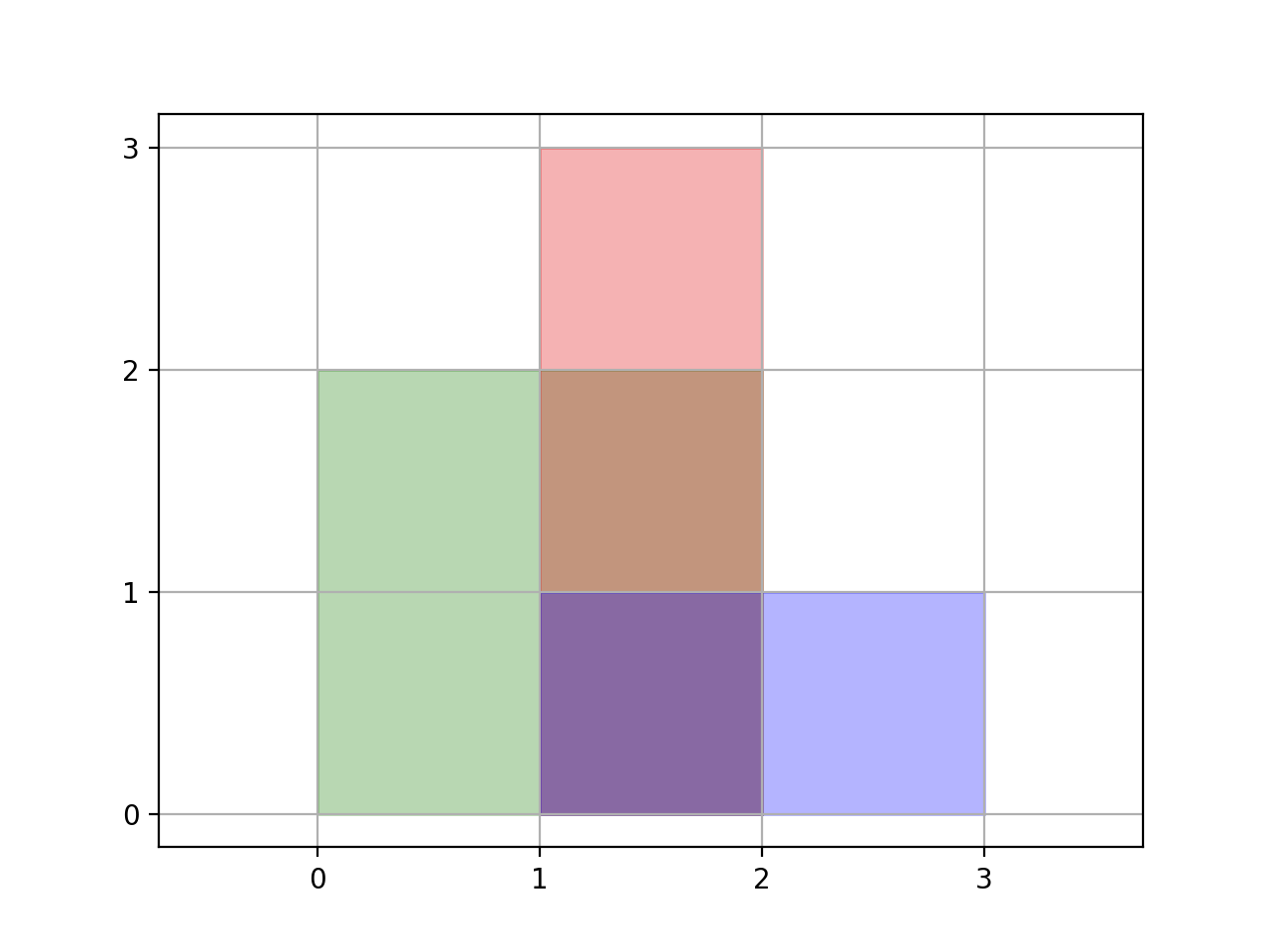
Input: [[0,0,2,2],[1,0,2,3],[1,0,3,1]] Output: 6 Explanation: As illustrated in the picture.
Example 2:
Input: [[0,0,1000000000,1000000000]] Output: 49 Explanation: The answer is 10^18 modulo (10^9 + 7), which is (10^9)^2 = (-7)^2 = 49.
1 <= rectangles.length <= 200rectanges[i].length = 40 <= rectangles[i][j] <= 10^9- The total area covered by all rectangles will never exceed
2^63 - 1and thus will fit in a 64-bit signed integer.
https://www.hackerearth.com/practice/math/geometry/line-sweep-technique/tutorial/
The events for this problem are the vertical edges.When we encounter a left edge, we do some action and when we encounter a right edge, we do some other action.Left edge is represented by lower-left point and right edge by upper-right point
We start our algorithm by sorting the events by x coordinates. When a lower left point of a rectangle is hit (i.e., we encounter left edge of rectangle), we insert the rectangle into the set . When we hit an upper right point of a rectangle (we encounter right edge of rectangle), we remove the rectangle from the set. At any instance, the set contains only the rectangles which intersect the sweep line (rectangles whose left edges are visited but right edges are not).
The area swept at any instance is = y * x where y is the length of the sweep line which is actually cut by the rectangle(s) (sum of the vertical lengths of the orange region, in the figure below) and x is the distance between two events of this sweep line.
But here we just know which are the rectangles intersecting the sweep line. So, here we have a new problem: how to find the length of the sweep line cut by the rectangles?
The solution to this problem is pretty the same we have been doing by now. We use the line sweep technique to find this but this time we apply it 90 degrees rotated, i.e., we sweep a horizontal line from bottom to up . The events for this sweep line would be the horizontal edges of the active rectangles(rectangles cut by vertical sweep line). When we encounter a bottom horizontal edge of an active rectangle, we increment the counter (counter here maintains the number of rectangles that overlap at current time) and we decrement it on top horizontal edge of active rectangle. When the counter becomes zero from some non zero value, we have found cut length of the vertical sweep line, so we add the area to our final answer.
Let's see it running now:







The images above show how we're doing the horizontal sweep bottom up. y is the sum of the length of the two arrows shown in the last image. This we do, for all events of vertical sweep line.
This was our algorithm. So, let's come to implementation part. For every event of vertical sweep line , we need to find the length of the cut on the sweep line, that means we need to go for horizontal sweep line. Here, we may use boolean array as our data structure because we would have once sorted the rectangles in order of vertical edges(vertical sweep) and once in order of horizontal edges(horizontal sweep), so we would have the sorting in both the directions.
The complexity of the algorithm can be easily seen to be . The complexity can be reduced by some other data structures such as BST instead of boolean array.
struct event
{
int ind; // Index of rectangle in rects
bool type; // Type of event: 0 = Lower-left ; 1 = Upper-right
event() {};
event(int ind, int type) : ind(ind), type(type) {};
};
struct point
{
int x, y;
};
point rects [MAX][12]; // Each rectangle consists of 2 points: [0] = lower-left ; [1] = upper-right
bool compare_x(event a, event b) { return rects[a.ind][a.type].x<rects[b.ind][b.type].x; }
bool compare_y(event a, event b) { return rects[a.ind][a.type].y<rects[b.ind][b.type].y; }
int union_area(event events_v[],event events_h[],int n,int e)
{
//n is the number of rectangles, e=2*n , e is the number of points (each rectangle has two points as described in declaration of rects)
bool in_set[MAX]={0};int area=0;
sort(events_v, events_v+e, compare_x); //Pre-sort of vertical edges
sort(events_h, events_h+e, compare_y); // Pre-sort set of horizontal edges
in_set[events_v[0].ind] = 1;
for (int i=1;i<e;++i)
{ // Vertical sweep line
event c = events_v[i];
int cnt = 0; // Counter to indicate how many rectangles are currently overlapping
// Delta_x: Distance between current sweep line and previous sweep line
int delta_x = rects[c.ind][c.type].x - rects[events_v[i-1].ind][events_v[i-1].type].x;
int begin_y;
if (delta_x==0){
in_set[c.ind] = (c.type==0);
continue;
}
for (int j=0;j<e;++j)
if (in_set[events_h[j].ind]==1) //Horizontal sweep line for active rectangle
{
if (events_h[j].type==0) //If it is a bottom edge of rectangle
{
if (cnt==0) begin_y = rects[events_h[j].ind][0].y; // Block starts
++cnt; //incrementing number of overlapping rectangles
}
else //If it is a top edge
{
--cnt; //the rectangle is no more overlapping, so remove it
if (cnt==0) //Block ends
{
int delta_y = (rects[events_h[j].ind][13].y-begin_y);//length of the vertical sweep line cut by rectangles
area+=delta_x * delta_y;
}
}
}
in_set[c.ind] = (c.type==0);//If it is a left edge, the rectangle is in the active set else not
}
return area;
}
http://www.cnblogs.com/scau20110726/archive/2013/04/12/3016765.html
1.矩形比较多,坐标也很大,所以横坐标需要离散化(纵坐标不需要),熟悉离散化后这个步骤不难,所以这里不详细讲解了,不明白的还请百度
2.重点:扫描线法:假想有一条扫描线,从左往右(从右往左),或者从下往上(从上往下)扫描过整个多边形(或者说畸形。。多个矩形叠加后的那个图形)。如果是竖直方向上扫描,则是离散化横坐标,如果是水平方向上扫描,则是离散化纵坐标。下面的分析都是离散化横坐标的,并且从下往上扫描的。
扫描之前还需要做一个工作,就是保存好所有矩形的上下边,并且按照它们所处的高度进行排序,另外如果是上边我们给他一个值-1,下边给他一个值1,我们用一个结构体来保存所有的上下边
struct segment
{
double l,r,h; //l,r表示这条上下边的左右坐标,h是这条边所处的高度
int f; //所赋的值,1或-1
}
{
double l,r,h; //l,r表示这条上下边的左右坐标,h是这条边所处的高度
int f; //所赋的值,1或-1
}
接着扫描线从下往上扫描,每遇到一条上下边就停下来,将这条线段投影到总区间上(总区间就是整个多边形横跨的长度),这个投影对应的其实是个插入和删除线段操作。还记得给他们赋的值1或-1吗,下边是1,扫描到下边的话相当于往总区间插入一条线段,上边-1,扫描到上边相当于在总区间删除一条线段(如果说插入删除比较抽象,那么就直白说,扫描到下边,投影到总区间,对应的那一段的值都要增1,扫描到上边对应的那一段的值都要减1,如果总区间某一段的值为0,说明其实没有线段覆盖到它,为正数则有,那会不会为负数呢?是不可能的,可以自己思考一下)。
每扫描到一条上下边后并投影到总区间后,就判断总区间现在被覆盖的总长度,然后用下一条边的高度减去当前这条边的高度,乘上总区间被覆盖的长度,就能得到一块面积,并依此做下去,就能得到最后的面积
http://tryalgo.org/en/geometry/2016/06/25/union-of-rectangles/
This problem can be solved in time using the sweep line algorithm. Sweep a vertical line from left to right over the rectangles. Divide the y axis into elementary y-intervals by considering all y coordinates from the input. Maintain a counter for each y-interval, which keeps track of how many rectangles currently cover this interval on the sweep line. These counters are index from 0 to say n-1, using the ordering along the y-axis. Whenever the sweep line reaches the left side of a rectangle, the counters need to be incremented at indices corresponding to included intervals. Whenever the sweep line reaches the right side of a rectangle this operation is inverted by decreasing the counters.
Now to keep track of the area of the union of rectangles over the part seen so far, we need to determine the total length over all intervals who’s counter is positive.
So we need a data structure that maintains an array of counters, each has an associated constant length. The data structure must implement the following operations.
- increment all entries between given indices i and j
- decrement all entries between given indices i and j
- query the total length of all intervals whose counter is positive.
The segment tree is the right choice for this data structure. It has complexity for the update operations and for the query. We need to augment the segment tree with a score per node, with the following properties.
- every node corresponds to a y-interval being the union of the elementary y-intervals over all the indices in the span of the node.
- if the node value is zero, the score is the sum of the scores of the descendants (or 0 if the node is a leaf).
- if the node value is positive, the score is the length of the y-interval corresponding to the node.
The sweep line algorithm consists of processing an event list. An event consists of a y-interval, a delta value +1 or -1 (left or right side), and an x-value. Events are ordered according to their x-values.
Approach #4: Segment Tree
As in Approach #3, we want to support
add(x1, x2), remove(x1, x2), and query(). While outside the scope of a typical interview, this is the perfect setting for using a segment tree. For completeness, we include the following implementation.
You can learn more about Segment Trees by visiting the articles of these problems: Falling Squares, Number of Longest Increasing Subsequence.
- Time Complexity: , where is the number of rectangles.
- Space Complexity: .
public int rectangleArea(int[][] rectangles) {
int OPEN = 1, CLOSE = -1;
int[][] events = new int[rectangles.length * 2][];
Set<Integer> Xvals = new HashSet();
int t = 0;
for (int[] rec : rectangles) {
events[t++] = new int[] { rec[1], OPEN, rec[0], rec[2] };
events[t++] = new int[] { rec[3], CLOSE, rec[0], rec[2] };
Xvals.add(rec[0]);
Xvals.add(rec[2]);
}
Arrays.sort(events, (a, b) -> Integer.compare(a[0], b[0]));
Integer[] X = Xvals.toArray(new Integer[0]);
Arrays.sort(X);
Map<Integer, Integer> Xi = new HashMap();
for (int i = 0; i < X.length; ++i)
Xi.put(X[i], i);
Node active = new Node(0, X.length - 1, X);
long ans = 0;
long cur_x_sum = 0;
int cur_y = events[0][0];
for (int[] event : events) {
int y = event[0], typ = event[1], x1 = event[2], x2 = event[3];
ans += cur_x_sum * (y - cur_y);
cur_x_sum = active.update(Xi.get(x1), Xi.get(x2), typ);
cur_y = y;
}
ans %= 1_000_000_007;
return (int) ans;
}
}
class Node {
int start, end;
Integer[] X;
Node left, right;
int count;
long total;
public Node(int start, int end, Integer[] X) {
this.start = start;
this.end = end;
this.X = X;
left = null;
right = null;
count = 0;
total = 0;
}
public int getRangeMid() {
return start + (end - start) / 2;
}
public Node getLeft() {
if (left == null)
left = new Node(start, getRangeMid(), X);
return left;
}
public Node getRight() {
if (right == null)
right = new Node(getRangeMid(), end, X);
return right;
}
public long update(int i, int j, int val) {
if (i >= j)
return 0;
if (start == i && end == j) {
count += val;
} else {
getLeft().update(i, Math.min(getRangeMid(), j), val);
getRight().update(Math.max(getRangeMid(), i), j, val);
}
if (count > 0)
total = X[end] - X[start];
else
total = getLeft().total + getRight().total;
return total;
}
数据范围很大,但分布很稀疏,比较裸的离散化了。
主要是判断离散化后的某个单独小块在原图中的面积比较麻烦,画个图就清楚了。
Approach #3: Line Sweep
https://leetcode.com/problems/rectangle-area-ii/discuss/139835/TopJava-Solution-with-detailed-explaination-check-this-one-!
Imagine we pass a horizontal line from bottom to top over the shape. We have some active intervals on this horizontal line, which gets updated twice for each rectangle. In total, there are events, and we can update our (up to ) active horizontal intervals for each update.
Algorithm
For a rectangle like
rec = [1,0,3,1], the first update is to add [1, 3] to the active set at y = 0, and the second update is to remove [1, 3] at y = 1. Note that adding and removing respects multiplicity - if we also added [0, 2] at y = 0, then removing [1, 3] at y = 1 will still leave us with [0, 2] active.
This gives us a plan: create these two events for each rectangle, then process all the events in sorted order of
y. The issue now is deciding how to process the events add(x1, x2) and remove(x1, x2) such that we are able to query() the total horizontal length of our active intervals.
We can use the fact that our
remove(...) operation will always be on an interval that was previously added. Let's store all the (x1, x2) intervals in sorted order. Then, we can query() in linear time using a technique similar to a classic LeetCode problem, Merge Intervals.- Time Complexity: , where is the number of rectangles.
- Space Complexity: .
added a sub class called
Interval, and used TreeMap for addition & removal, which should reduce both operations complexity to O(logn).- order every line from the rectangle by y index. mark start of rectangle line (bottom) as OPEN, mark end of rectangle line (top) as CLOSE.
- sweep line from bottom to top, each time y coordinate changed, means all intervals on current y is sweeped, merge the length back together, multiply by the y coordinate diff.
private static class Interval {
public int start;
public int end;
public Interval(int start, int end) {
this.start = start;
this.end = end;
}
}
public int rectangleArea(int[][] rectangles) {
int OPEN = 0, CLOSE = 1;
int[][] events = new int[rectangles.length * 2][4];
int t = 0;
/**
open of rectangle: add to active set
close of rectangle: remove from active set
*/
for (int[] rec: rectangles) {
// y, open_or_close, start, end
events[t++] = new int[]{ rec[1], OPEN, rec[0], rec[2] };
events[t++] = new int[]{ rec[3], CLOSE, rec[0], rec[2] };
}
/**
sort by current y index
*/
Arrays.sort(events, (a, b) -> Integer.compare(a[0], b[0]));
TreeMap<Interval, Integer> active = new TreeMap<>((a, b) -> {
if (a.start != b.start) return a.start - b.start;
return a.end - b.end;
});
// first y coordinate at the bottom
int currentY = events[0][0];
long ans = 0;
for (int[] event : events) {
int y = event[0], typ = event[1], x1 = event[2], x2 = event[3];
// Calculate sum of intervals in active set, that's the active intervals in prev line
if (y > currentY) {
ans += calculateInterval(active) * (y - currentY);
currentY = y;
}
/**
add or remove new interval to current active
*/
if (typ == OPEN) {
addInterval(active, x1, x2);
} else {
removeInterval(active, x1, x2);
}
}
ans %= 1_000_000_007;
return (int) ans;
}
/**
using tree map, should be able to insert in logn time
*/
private void addInterval(TreeMap<Interval, Integer> map, int x1, int x2) {
Interval interval = new Interval(x1, x2);
map.put(interval, map.getOrDefault(interval, 0) + 1);
}
/**
using tree map, should be able to remove in logn time
*/
private void removeInterval(TreeMap<Interval, Integer> map, int x1, int x2) {
Interval interval = new Interval(x1, x2);
map.put(interval, map.getOrDefault(interval, 0) - 1);
if (map.get(interval) == 0) map.remove(interval);
}
private long calculateInterval(TreeMap<Interval, Integer> map) {
long query = 0;
int cur = -1;
for (Interval interval : map.keySet()) {
cur = Math.max(cur, interval.start);
query += Math.max(interval.end - cur, 0);
cur = Math.max(cur, interval.end);
}
return query;
}X. https://www.hackerearth.com/practice/math/geometry/line-sweep-technique/practice-problems/algorithm/area-of-rectangles/editorial/
This problem is one of the most basic applications of line sweep. We plan to sweep a vertical line from to , while maintaining some data structure to know which rectangles are currently contributing to the total area. Notice that , and hence an would also work in time!
Let's define rectangles by their left and right boundaries. Hence, a rectangle would be defined as starting at [,{}] and ending at [,{}]. Now, for every , we know information about all rectangles starting and ending at that point. This is our list of events.
Now, you just need to sweep over the range of x, and at every step add the count of y such that there is a rectangle covering that at this point. Refer to setter and tester solutions for more information on how to maintain such a data structure.
This problem can also be done in , by keeping a segment tree instead of arrays.
Let's define rectangles by their left and right boundaries. Hence, a rectangle would be defined as starting at [,{}] and ending at [,{}]. Now, for every , we know information about all rectangles starting and ending at that point. This is our list of events.
Now, you just need to sweep over the range of x, and at every step add the count of y such that there is a rectangle covering that at this point. Refer to setter and tester solutions for more information on how to maintain such a data structure.
This problem can also be done in , by keeping a segment tree instead of arrays.
scanf("%d", &n);for (int i=0;i<n;++i){scanf("%d %d %d %d", &rects[i][0].x, &rects[i][0].y,&rects[i][1].x, &rects[i][1].y);events_v[e] = event(i, 0);events_h[e++] = event(i, 0);events_v[e] = event(i, 1);events_h[e++] = event(i, 1);}sort(events_v, events_v+e, compare_x);sort(events_h, events_h+e, compare_y);in_set[events_v[0].ind] = 1;for (int i=1;i<e;++i){event c = events_v[i];int cnt = 0;int delta_x = rects[c.ind][c.type].x - rects[events_v[i-1].ind][events_v[i-1].type].x;int begin_y;if (delta_x==0){in_set[c.ind] = (c.type==0);continue;}for (int j=0;j<e;++j)if (in_set[events_h[j].ind]==1){if (events_h[j].type==0){if (cnt==0) begin_y = rects[events_h[j].ind][0].y;++cnt;}else{--cnt;if (cnt==0){int delta_y = (rects[events_h[j].ind][1].y-begin_y);area+=(ll)delta_x * (ll)delta_y;}}}in_set[c.ind] = (c.type==0);}printf("%lld\n", area);
Approach #2: Coordinate Compression
Suppose instead of
rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]], we had [[0,0,200,200],[100,0,200,300],[100,0,300,100]]. The answer would just be 100 times bigger.
What about if
rectangles = [[0,0,2,2],[1,0,2,3],[1,0,30002,1]] ? Only the blue region would have area 30000 instead of 1.
Our idea is this: we'll take all the
x and y coordinates, and re-map them to 0, 1, 2, ... etc. For example, if rectangles = [[0,0,200,200],[100,0,200,300],[100,0,300,100]], we could re-map it to [[0,0,2,2],[1,0,2,3],[1,0,3,1]]. Then, we can solve the problem with brute force. However, each region may actually represent some larger area, so we'll need to adjust for that at the end.
Algorithm
Re-map each
x coordinate to 0, 1, 2, .... Independently, re-map all y coordinates too.
We then have a problem that can be solved by brute force: for each rectangle with re-mapped coordinates
(rx1, ry1, rx2, ry2), we can fill the grid grid[x][y] = True for rx1 <= x < rx2 and ry1 <= y < ry2.
Afterwards, each
grid[rx][ry] represents the area (imapx(rx+1) - imapx(rx)) * (imapy(ry+1) - imapy(ry)), where if x got remapped to rx, then imapx(rx) = x ("inverse-map-x of remapped-x equals x"), and similarly for imapy.- Time Complexity: , where is the number of rectangles.
- Space Complexity: .
public int rectangleArea(int[][] rectangles) {
int N = rectangles.length;
Set<Integer> Xvals = new HashSet();
Set<Integer> Yvals = new HashSet();
for (int[] rec : rectangles) {
Xvals.add(rec[0]);
Xvals.add(rec[2]);
Yvals.add(rec[1]);
Yvals.add(rec[3]);
}
Integer[] imapx = Xvals.toArray(new Integer[0]);
Arrays.sort(imapx);
Integer[] imapy = Yvals.toArray(new Integer[0]);
Arrays.sort(imapy);
Map<Integer, Integer> mapx = new HashMap();
Map<Integer, Integer> mapy = new HashMap();
for (int i = 0; i < imapx.length; ++i)
mapx.put(imapx[i], i);
for (int i = 0; i < imapy.length; ++i)
mapy.put(imapy[i], i);
boolean[][] grid = new boolean[imapx.length][imapy.length];
for (int[] rec : rectangles)
for (int x = mapx.get(rec[0]); x < mapx.get(rec[2]); ++x)
for (int y = mapy.get(rec[1]); y < mapy.get(rec[3]); ++y)
grid[x][y] = true;
long ans = 0;
for (int x = 0; x < grid.length; ++x)
for (int y = 0; y < grid[0].length; ++y)
if (grid[x][y])
ans += (long) (imapx[x + 1] - imapx[x]) * (imapy[y + 1] - imapy[y]);
ans %= 1_000_000_007;
return (int) ans;
}
https://blog.csdn.net/u011439455/article/details/80665208?utm_source=blogxgwz8思路是将坐标映射缩小范围,然后暴力标记,之后映射回去计算面积
Approach #1: Principle of Inclusion-Exclusion
Say we have two rectangles, and . The area of their union is:
Say we have three rectangles, . The area of their union is:
This can be seen by drawing a Venn diagram.
Say we have four rectangles, . The area of their union is:
In general, the area of the union of rectangles will be:
Algorithm
If we do not know the above fact, we can prove it by considering any point in . Say this point occurs in all , and let . Then on the right side, it is counted times. By considering the binomial expansion of , this is in fact equal to .
From Rectangle Area I, we know that the intersection of two axis-aligned rectangles is another axis-aligned rectangle (or nothing). So in particular, the intersection is always a rectangle (or nothing).
Now our algorithm proceeds as follows: for every subset of (where is the number of rectangles), we'll calculate the intersection of the rectangles in that subset , and then the area of that rectangle. This allows us to calculate algorithmically the right-hand side of the general equation we wrote earlier.
- Time Complexity: , where is the number of rectangles.
- Space Complexity: .
public int rectangleArea(int[][] rectangles) {
int N = rectangles.length;
long ans = 0;
for (int subset = 1; subset < (1 << N); ++subset) {
int[] rec = new int[] { 0, 0, 1_000_000_000, 1_000_000_000 };
int parity = -1;
for (int bit = 0; bit < N; ++bit)
if (((subset >> bit) & 1) != 0) {
rec = intersect(rec, rectangles[bit]);
parity *= -1;
}
ans += parity * area(rec);
}
long MOD = 1_000_000_007;
ans %= MOD;
if (ans < 0)
ans += MOD;
return (int) ans;
}
public long area(int[] rec) {
long dx = Math.max(0, rec[2] - rec[0]);
long dy = Math.max(0, rec[3] - rec[1]);
return dx * dy;
}
public int[] intersect(int[] rec1, int[] rec2) {
return new int[] { Math.max(rec1[0], rec2[0]), Math.max(rec1[1], rec2[1]), Math.min(rec1[2], rec2[2]),
Math.min(rec1[3], rec2[3]), };
}
- Add the new rectangle into a LinkedList
listone by one. - traverse all previous rectangles in list and check whether is any overlap area between the new rectangle and existing one.
- if yes, , remove the existing rectangle from list and split it into at most 4 new rectangles without the overlap area, using a
cachelist to avoid the Fail-fast exception. - add these new rectangles into
list.
public int rectangleArea(int[][] rectangles) {
List<int[]> list = new LinkedList<>();
long sum = 0;
for (int[] cur : rectangles) {
sum += join(list, cur);
sum = sum % (1000000007);
}
return (int)sum;
}
public long join(List<int[]> list, int[] cur) {
if (list.size() == 0) {
list.add(cur);
return area(cur);
}
Iterator<int[]> iter = list.iterator();
List<int[]> cache = new LinkedList<>();
long sum = 0;
while (iter.hasNext()) {
int[] tmp = iter.next();
if (cur[2] >= tmp[0] && cur[0] <= tmp[2] && cur[3] >= tmp[1] && cur[1] <= tmp[3]) {
sum -= area(tmp);
iter.remove();
if (cur[0] > tmp[0])
cache.add(new int[]{tmp[0], tmp[1], cur[0], tmp[3]});
if (cur[3] < tmp[3])
cache.add(new int[]{Math.max(cur[0], tmp[0]), cur[3], tmp[2], tmp[3]});
if (cur[1] > tmp[1])
cache.add(new int[]{Math.max(cur[0], tmp[0]), tmp[1], tmp[2], cur[1]});
if (cur[2] < tmp[2])
cache.add(new int[]{cur[2], Math.max(tmp[1], cur[1]), tmp[2], Math.min(cur[3], tmp[3])});
}
}
cache.add(cur);
for (int[] x : cache) {
list.add(x);
sum += area(x);
sum = sum % 1000000007;
}
return sum;
}
public long area(int[] cur) {
return ((cur[2] - cur[0]) * (long)(cur[3] - cur[1])) % 1000000007;
}
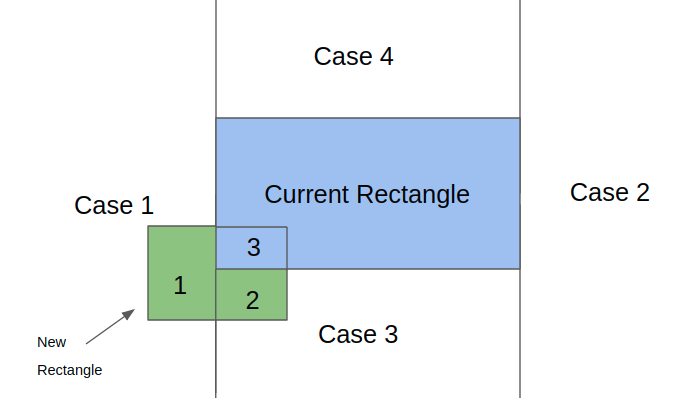
The idea here is to maintain a list of non-overlapping rectangles to calculate final area.
If a new rectangle does not overlap with any of the existing rectanlges, add it to the list.
If there is an overlap, split the non-overlapping regions of the rectangle into smaller rectangles and compare with the rest of the list.
If a new rectangle does not overlap with any of the existing rectanlges, add it to the list.
If there is an overlap, split the non-overlapping regions of the rectangle into smaller rectangles and compare with the rest of the list.
For example, when a new rectangle (green) is compared with the current rectangle (blue), the non-overlapping regions can be split into two smaller rectangles. Rectangle 1 will be covered by the first overlapping case in addRectangle() and rectangle 2 will be covered by the third case. Rectangle 3 overlaps with the current rectangle and need not be considered.

https://www.cnblogs.com/sfzyk/p/9321181.html
算法1 朴素思想 虽然朴素但是代码却有意思
利用容斥原理
复杂度高达 N*2^N
利用容斥原理
复杂度高达 N*2^N
def intersect(rec1,rec2):
return [max(rec1[1],rec2[1]),
max(rec1[2],rec2[2]),
min(rec1[3],rec2[3]),
min(rec1[4],rec2[4]
]
#这里是两个矩形的两点式求 矩形的相交子矩形 *非常值得思考
def area(rec):
dx=max(0,rec[2]-rec[0])
dy=max(0,rec[3]-rec[1])
return dx*dy
ans=0
for size in range(1,len(rectangles)+1):
for group in itertools.combinations(rectangles,size):
ans = ans +(-1)** (size+1) * area(reduce(intersect,group))
return ans%mod
https://www.gjxhlan.me/2018/06/10/leetcode-contest-88-solution/
- 第一种按纵轴 y 扫一遍,每次求两条 y 边之间的 area 和。
- 第二种是每次读矩阵,用一个 list 存储所有不重叠的矩阵,当新矩阵 r 和 list 中的矩阵重合时,将 list 中的矩阵和 r 重叠的部分拆除,将 list 中的矩阵拆分成多个矩阵(最多4个),然后将 r 存入 list,这种方法的时间惊人的短。
https://blog.csdn.net/Bob__yuan/article/details/81394230
Find the total area covered by two rectilinear rectangles in a 2D plane.
Each rectangle is defined by its bottom left corner and top right corner as shown in the figure.
int computeArea(int A, int B, int C, int D, int E, int F, int G, int H)
{
int cross = 0; // 重叠区域
int top = min(D, H), bottom = max(B, F), left = max(A, E), right = min(C, G);
if(top > bottom && left < right)
cross = (top - bottom) * (right - left);
return (((C - A) * (D - B)) + ((G - E) * (H - F)) - cross);
}
