Related:
LeetCode 924 - Minimize Malware Spread
LeetCode 928 - Minimize Malware Spread II
https://leetcode.com/problems/minimize-malware-spread-ii/
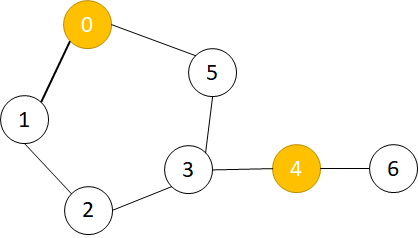
as picture shows, the yellow node is the initial infected node.
for the safe node [1,2,3,5,6], we analyze one by one.
def dfs(self, from_, g, vis, ini_):
X. BFS
http://hehejun.blogspot.com/2018/10/leetcodeminimize-malware-spread-ii.html
http://www.noteanddata.com/leetcode-928-Minimize-Malware-Spread-II-java-solution-note-2.html
LeetCode 924 - Minimize Malware Spread
LeetCode 928 - Minimize Malware Spread II
https://leetcode.com/problems/minimize-malware-spread-ii/
(This problem is the same as Minimize Malware Spread, with the differences bolded.)
In a network of nodes, each node
i is directly connected to another node j if and only if graph[i][j] = 1.
Some nodes
initial are initially infected by malware. Whenever two nodes are directly connected and at least one of those two nodes is infected by malware, both nodes will be infected by malware. This spread of malware will continue until no more nodes can be infected in this manner.
Suppose
M(initial) is the final number of nodes infected with malware in the entire network, after the spread of malware stops.
We will remove one node from the initial list, completely removing it and any connections from this node to any other node. Return the node that if removed, would minimize
M(initial). If multiple nodes could be removed to minimize M(initial), return such a node with the smallest index.
Example 1:
Input: graph = [[1,1,0],[1,1,0],[0,0,1]], initial = [0,1] Output: 0
Example 2:
Input: graph = [[1,1,0],[1,1,1],[0,1,1]], initial = [0,1] Output: 1
Example 3:
Input: graph = [[1,1,0,0],[1,1,1,0],[0,1,1,1],[0,0,1,1]], initial = [0,1] Output: 1
Approach 2: Union-Find
https://leetcode.com/problems/minimize-malware-spread-ii/discuss/187715/C%2B%2B
https://www.acwing.com/solution/leetcode/content/583/
https://leetcode.com/problems/minimize-malware-spread-ii/discuss/187715/C%2B%2B
https://www.acwing.com/solution/leetcode/content/583/
首先我们先将所有的病毒节点去掉,然后将所有连通块合并成一个节点。
这是因为一个连通块中的节点,要么全部被感染,要么全部不被感染,所以我们可以将它们当成一个整体来考虑。
这是因为一个连通块中的节点,要么全部被感染,要么全部不被感染,所以我们可以将它们当成一个整体来考虑。
然后我们统计一下所有连通块,直接相邻的病毒节点的个数。
对于一个连通块:
对于一个连通块:
- 如果直接相邻的病毒节点的个数为0,则一定不会被感染,忽略之;
- 如果直接相邻的病毒节点的个数为1,则将该病毒节点删除后,整个连通块就可以避免被感染;
- 如果直接相邻的病毒节点的个数大于等于2,则不管删除哪个病毒节点,该连通块都仍会被感染,忽略之;
所以我们只需在所有第二种连通块(直接相邻的病毒节点的个数为1的连通块)中,找出节点个数最多的连通块,与它相邻的病毒节点就是我们要删除的节点;如果有多个连通块节点个数相同,我们找出与之对应的编号最小的病毒节点即可。
时间复杂度分析:
- 合并所有非病毒节点的连通块:O(n²);
- 统计每个连通块节点的个数:O(n) ;
- 统计每个连通块连接的病毒节点个数:O(n²);
- 遍历所有连通块,求需要删除的节点:O(n) ;
所以总时间复杂度是 O(n²)。
vector<int> p;
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int minMalwareSpread(vector<vector<int>>& graph, vector<int>& initial) {
unordered_set<int> S;
for (auto v : initial) S.insert(v);
int n = graph.size();
for (int i = 0; i < n; i ++ ) p.push_back(i); // 初始化并查集
for (int i = 0; i < n; i ++ ) // 合并所有没有被病毒感染的点
for (int j = 0; j < n; j ++ )
if (S.count(i) == 0 && S.count(j) == 0 && graph[i][j])
{
p[find(i)] = find(j);
}
unordered_map<int, int> comp_cnt; // 统计每个连通块的节点个数
for (int i = 0; i < n; i ++ )
if (S.count(i) == 0)
comp_cnt[find(i)] ++ ;
unordered_map<int, unordered_set<int>> comp_infect; // 统计每个连通块连接的病毒节点个数
for (auto i : initial)
for (int j = 0; j < n; j ++ )
if (S.count(j) == 0 && graph[i][j])
comp_infect[find(j)].insert(i);
int m = -1, res = initial[0];
for (auto v : initial) res = min(res, v);
for (auto item : comp_infect)
{
if (item.second.size() == 1)
{
int ver = *item.second.begin();
int cnt = comp_cnt[item.first];
if (cnt > m)
{
m = cnt;
res = ver;
}
else if (cnt == m && res > ver)
res = ver;
}
}
return res;
}
Let
G be the graph with all the nodes in initial removed. For each component of G, either it neighbors 0, 1, or >= 2 nodes from initial. The result only changes if there is exactly 1 neighbor from initial, so we need a way to count this.
Algorithm
It is clear that we will need to consider components of the graph. A "Disjoint Set Union" (DSU) data structure is ideal for this.
We will skip the explanation of how a DSU structure is implemented. Please refer to https://leetcode.com/problems/redundant-connection/solution/ for a tutorial on DSU.
As above, lets consider the components of
G: the graph without any nodes from initial.
Then, for every edge
uv in the original graph, where u is in initial and v is not, we can count that the component at v of G neighbors 1 more infected node.
Now, for each node
u in initial, for each component of G it neighbors, if that component would only be infected by u ("uniquely infected"), then the size of that component contributes to the answer for removing u.
We take the best possible answer.
- Time Complexity: , where is the length of
graph, as the graph is given in adjacent matrix form. - Space Complexity: .
public int minMalwareSpread(int[][] graph, int[] initial) {
int N = graph.length;
DSU dsu = new DSU(N);
// clean[u] == 1 if its a node in the graph not in initial.
int[] clean = new int[N];
Arrays.fill(clean, 1);
for (int x : initial)
clean[x] = 0;
for (int u = 0; u < N; ++u)
if (clean[u] == 1)
for (int v = 0; v < N; ++v)
if (clean[v] == 1)
if (graph[u][v] == 1)
dsu.union(u, v);
// dsu now represents the components of the graph without
// any nodes from initial. Let's call this graph G.
int[] count = new int[N];
Map<Integer, Set<Integer>> nodeToCompo = new HashMap();
for (int u : initial) {
Set<Integer> components = new HashSet();
for (int v = 0; v < N; ++v)
if (clean[v] == 1) {
if (graph[u][v] == 1)
components.add(dsu.find(v));
}
nodeToCompo.put(u, components);
for (int c : components)
count[c]++;
}
// For each node u in initial, nodeToCompo.get(u)
// now has every component from G that u neighbors.
int ans = -1, ansSize = -1;
for (int u : nodeToCompo.keySet()) {
Set<Integer> components = nodeToCompo.get(u);
int score = 0;
for (int c : components)
if (count[c] == 1) // uniquely infected
score += dsu.size(c);
if (score > ansSize || score == ansSize && u < ans) {
ansSize = score;
ans = u;
}
}
return ans;
}
}
class DSU {
int[] p, sz;
DSU(int N) {
p = new int[N];
for (int x = 0; x < N; ++x)
p[x] = x;
sz = new int[N];
Arrays.fill(sz, 1);
}
public int find(int x) {
if (p[x] != x)
p[x] = find(p[x]);
return p[x];
}
public void union(int x, int y) {
int xr = find(x);
int yr = find(y);
p[xr] = yr;
sz[yr] += sz[xr];
}
public int size(int x) {
return sz[find(x)];
}
The key point of these two questions is to analyze how to change a node from an infected state to a safe one.

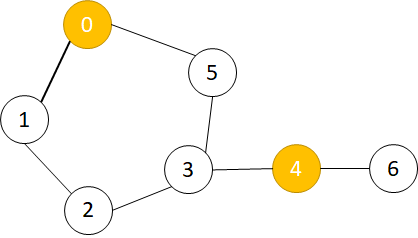
as picture shows, the yellow node is the initial infected node.
for the safe node [1,2,3,5,6], we analyze one by one.
we define
node a are directly infected by node b if node a will be infected by node b without through any other infected node.
For
For
For
For
For
node 1, it will be directly infected by node 0 and node 4,(0->1, 4->3->2->1)For
node 2, it is same as node 1(0->1->2, 4->3->2)For
node 3, it is same as node 1For
node 5, it is same as node 1For
node 6, it will be directly infected by node 4. (4 - > 6)
for node [1,2,3,5], even if we delete one node from the initial infected node, it will be infected by another node in the end.
So, a node may be safe if and only if it's just
we can use bfs solution to find the all
Finally, we count which node in the stored node appears the most.
directly infected by one node. I called it s_nodewe can use bfs solution to find the all
s_node, and store the only node that can infect it.Finally, we count which node in the stored node appears the most.
def minMalwareSpread(self, graph, initial):
n = len(graph)
d = collections.defaultdict(list)
for init in initial:
vis = set(initial)
Q = collections.deque([init])
while Q:
infect = Q.popleft()
for node in range(len(graph[infect])):
if graph[infect][node] == 0: continue
if node in vis: continue
vis.add(node)
d[node].append(init)
Q.append(node)
# count the most frequent node
res = [0] * n
for key in d:
if len(d[key]) == 1:
res[d[key][0]] += 1
if max(res) == 0: return min(initial)
return res.index(max(res))
Approach 1: Depth First Search
Let
G be the graph with all the nodes from initial removed.
For each node
v not in initial, we want to know which nodes u from initial can reach v in the graph G [with u (and its edges) added to G]. Let's say these nodes u "infect" v.
Afterwards, we want to know which nodes
v are uniquely infected by only one u. For each such pair, it contributes 1 to the answer for u.- Time Complexity: , where is the length of
graph, as the graph is given in adjacent matrix form. - Space Complexity: .
public int minMalwareSpread(int[][] graph, int[] initial) {
int N = graph.length;
int[] clean = new int[N];
Arrays.fill(clean, 1);
for (int x : initial)
clean[x] = 0;
// For each node u in initial, dfs to find
// 'seen': all nodes not in initial that it can reach.
ArrayList<Integer>[] infectedBy = new ArrayList[N];
for (int i = 0; i < N; ++i)
infectedBy[i] = new ArrayList();
for (int u : initial) {
Set<Integer> seen = new HashSet();
dfs(graph, clean, u, seen);
for (int v : seen)
infectedBy[v].add(u);
}
// For each node u in initial, for every v not in initial
// that is uniquely infected by u, add 1 to the contribution for u.
int[] contribution = new int[N];
for (int v = 0; v < N; ++v)
if (infectedBy[v].size() == 1)
contribution[infectedBy[v].get(0)]++;
// Take the best answer.
Arrays.sort(initial);
int ans = initial[0], ansSize = -1;
for (int u : initial) {
int score = contribution[u];
if (score > ansSize || score == ansSize && u < ans) {
ans = u;
ansSize = score;
}
}
return ans;
}
public void dfs(int[][] graph, int[] clean, int u, Set<Integer> seen) {
for (int v = 0; v < graph.length; ++v)
if (graph[u][v] == 1 && clean[v] == 1 && !seen.contains(v)) {
seen.add(v);
dfs(graph, clean, v, seen);
}
}
Idea is that, first, we disable all the nodes from initial list. And build the union find set.
Then we try removing each node from the initial list in way of brute-force .
Say in this trial, we will remove initial[i]. We execute the trial by marking all the components linked by the elements from the init list except initial[i]. Then we sum up the number of all the linked components at the end of the trial, we compare the sum to a global_min. Hence we may find a node that results in a minimum M(initial)
Say in this trial, we will remove initial[i]. We execute the trial by marking all the components linked by the elements from the init list except initial[i]. Then we sum up the number of all the linked components at the end of the trial, we compare the sum to a global_min. Hence we may find a node that results in a minimum M(initial)
Note in my implementation of UFS, I use a parent array. In my array, if a node is not root, then its value is its parent index, else if this is a root, its value equals negative (number of this component). Hence we may mark the root node and the parent relationship using only one value.
(Check this out if you don't know UFS: https://zh.wikipedia.org/wiki/并查集)
int[] parent;
public int minMalwareSpread(int[][] graph, int[] initial) {
int N = graph.length;
parent = new int[N];
Arrays.fill(parent, -1);
Arrays.sort(initial); // sort the initial list to get the min index of result in case of a tie
Set<Integer> set = new HashSet<>();
for (int n : initial) set.add(n);
// build the union find set disabling the init elements
for (int i = 0; i < N; i++) {
if (set.contains(i)) continue;
for (int j = 0; j < N; j++) {
if (set.contains(j)) continue;
if (graph[i][j] == 1) {
union(i, j);
}
}
}
int total = Integer.MAX_VALUE;
int res = -1;
for (int skip = 0; skip < initial.length; skip++) {
Map<Integer, Integer> cnts = new HashMap<>();
for (int mal = 0; mal < initial.length; mal++) {
if (mal == skip) continue;
int malId = initial[mal];
for (int i = 0; i < N; i++) {
if (i == initial[skip]) continue;
if (graph[malId][i] == 1) {
int root = find(i);
cnts.putIfAbsent(root, -parent[root]);
}
}
}
int sum = 0;
for (int v : cnts.values()) {
sum += v;
}
// if removing initial[skip] causes less spread
if (sum < total) {
total = sum;
res = initial[skip];
}
}
return res;
}
private int find(int x) {
if (parent[x] < 0) return x;
parent[x] = find(parent[x]);
return parent[x];
}
private void union(int x, int y) {
x = find(x);
y = find(y);
if (x == y) return;
if (parent[x] <= parent[y]) {
parent[x] += parent[y];
parent[y] = x;
} else {
parent[y] += parent[x];
parent[x] = y;
}
}
https://zhanghuimeng.github.io/post/leetcode-928-minimize-malware-spread-ii/
优化过的DFS
https://www.hrwhisper.me/leetcode-contest-107-solution/
呃,这道题的题意正好和我上次看错的是一样的……于是我当然直接用了最暴力的方法,手动模拟每个初始感染结点被删除之后的感染状况。当然我觉得这种方法看起来还不差,因为DFS的复杂度是
O(N),DFSN次的复杂度就是O(N^2);不过显然我这样想的时候没有考虑到题目里给出的图是邻接矩阵表示(而非邻接表),所以实际复杂度应该是O(N^3)。不过反正N <= 300,N^2和N^3也差不多。(……)优化过的DFS
首先将所有初始感染结点从图里移除;然后对于每个初始感染结点,通过DFS找到它能够感染的结点集合;然后对于每个普通结点,找出它会被多少个结点感染。如果它只能被某一个结点感染,移除该结点就可以使得该普通结点不会被感染。然后找到其中的最大值即可。[1]
我的一个疑惑是,为何是把所有初始感染结点都移除,而不是把所有的结点都留在图里,然后找到某一个结点能感染的结点集合?这两点的区别显然是,把其他的结点留在图里之后,某一个结点能感染的结点集合就会变大,甚至包含一些移除了别的结点之后不能被感染的结点,这大约是不合适的。
另一个问题是,考虑到邻接矩阵的问题,这个方法的时间复杂度是不是仍然是
O(N^3)……事实证明运行时间差不多。void dfs(int cur, vector<vector<int>>& graph, int &cnt, const int& removed, bool visited[]) { for (int y = 0; y < graph[cur].size(); y++) { if (graph[cur][y] && !visited[y] && y != removed) { visited[y] = true; cnt++; dfs(y, graph, cnt, removed, visited); } } } public: int minMalwareSpread(vector<vector<int>>& graph, vector<int>& initial) { // completely remove sort(initial.begin(), initial.end()); int n = graph.size(); int ans = n + 1, index = -1; bool visited[n]; for (int x: initial) { memset(visited, false, sizeof(visited)); int cnt = 0; for (int y: initial) { if (x != y && !visited[y]) { visited[y] = true; cnt++; dfs(y, graph, cnt, x, visited); } } if (cnt < ans) { index = x; ans = cnt; } } return index; }
优化过的DFS
void dfs(int cur, const int& x, vector<vector<int>>& graph, bool isRemoved[], unordered_set<int> affect[]) { for (int i = 0; i < graph.size(); i++) { if (graph[cur][i] && !isRemoved[i] && affect[x].find(i) == affect[x].end()) { affect[x].insert(i); dfs(i, x, graph, isRemoved, affect); } } } public: int minMalwareSpread(vector<vector<int>>& graph, vector<int>& initial) { int n = graph.size(); bool isRemoved[n]; memset(isRemoved, 0, sizeof(isRemoved)); for (int x: initial) isRemoved[x] = true; // 分别DFS unordered_set<int> affect[n]; for (int x: initial) { isRemoved[x] = false; affect[x].insert(x); dfs(x, x, graph, isRemoved, affect); isRemoved[x] = true; } // 每个结点会被哪些结点感染 unordered_set<int> affectedBy[n]; for (int i = 0; i < n; i++) { for (int x: affect[i]) affectedBy[x].insert(i); } // 只被一个结点感染的结点 int singleCnt[n]; memset(singleCnt, 0, sizeof(singleCnt)); for (int i = 0; i < n; i++) { if (!isRemoved[i] && affectedBy[i].size() == 1) singleCnt[*affectedBy[i].begin()]++; } // 取最大值 int index = -1, maximum = -1; for (int i = 0; i < n; i++) { if (isRemoved[i] && singleCnt[i] > maximum) { index = i; maximum = singleCnt[i]; } } return index; }
https://www.hrwhisper.me/leetcode-contest-107-solution/
思路:和924题类似,那题可以贪心的计算出某个结点最大可达的结点个数,这题就计算去掉之后被感染的,然后找最小的即可。
def dfs(self, from_, g, vis, ini_):
vis[from_] = True
for to in range(len(g[from_])):
if not g[from_][to] or vis[to] or to == ini_:
continue
self.dfs(to, g, vis, ini_)
def minMalwareSpread(self, graph, initial):
"""
:type graph: List[List[int]]
:type initial: List[int]
:rtype: int
"""
cnt = [0] * len(graph)
initial.sort()
for ini_ in initial:
vis = [False] * len(graph)
for i in initial:
if i != ini_:
self.dfs(i, graph, vis, ini_)
cnt[ini_] = sum(vis)
min_node = initial[0]
for node in initial:
if cnt[node] < cnt[min_node]:
min_node = node
return min_node
http://hehejun.blogspot.com/2018/10/leetcodeminimize-malware-spread-ii.html
http://www.noteanddata.com/leetcode-928-Minimize-Malware-Spread-II-java-solution-note-2.html
- 这里主要的区别是重复的部分, 也就是两个initial会连到一起,然后污染同一批机器
假如有如下图, 然后initial是[1,5]
如果删除1, 就是剩下5,被感染的机器是[2,3,4,5,6]
如果删除5, 就是剩下1,被感染的机器是[1,2,3,4]
1---2---3---4
|
|
5---6
从这个例子可以看出,有一些节点可能会被两个initial都感染到,而有一些节点只能被某一些initial感染到。
如果移除某个initial并且把相关的连接都切断以后, 那么那些只能被这个initial感染的节点就不能被感染, 这实际上就是真正被移除的节点。
如果移除某个initial并且把相关的连接都切断以后, 那么那些只能被这个initial感染的节点就不能被感染, 这实际上就是真正被移除的节点。
- 所以, 可以bfs访问每个initial节点,然后看只能被这个节点感染的节点有哪些。
a. 如果在bfs的过程中遇到其他initial节点就不访问
b. 如果任意某一个节点被一个initial节点访问到过,那就不算是“只能被某个initial节点感染的节点”, 应该从记录中删除
public int minMalwareSpread(int[][] graph, int[] initial) {
Set<Integer> initialSet = new HashSet<>();
for(int node: initial) {
initialSet.add(node);
}
Map<Integer,Integer> uniqueSourceMap = new HashMap<>();
Set<Integer> uniqueSourceSet = new HashSet<>();
for(int node: initial) {
Set<Integer> visited = new HashSet<>();
Queue<Integer> queue = new LinkedList<>();
queue.add(node);
while(queue.size() > 0) {
int v = queue.poll();
visited.add(v);
if(!uniqueSourceSet.contains(v)) {
uniqueSourceSet.add(v);
uniqueSourceMap.put(v, node);
}
else {
uniqueSourceMap.remove(v);
}
for(int i = 0; i < graph.length; ++i) {
if(graph[v][i] == 1 && !initialSet.contains(i) && !visited.contains(i)) {
queue.add(i);
}
}
}
}
int[] countTable = new int[graph.length];
int maxi = 0;
for(Map.Entry<Integer, Integer> entry: uniqueSourceMap.entrySet()) {
int i = entry.getValue();
countTable[i]++;
if(countTable[i] > countTable[maxi]) maxi = i;
else if(countTable[i] == countTable[maxi] && i < maxi) maxi = i;
}
return maxi;
}
这道题Brute Force的做法就可以,我们依次把每个节点从initial list和图中移除,然后bfs看最后能够感染多少节点,取最少的就是答案。时间复杂度O((V + E) * N),V为节点数,E为边数,N为initial list的长度
这道题关键点在于想到,要想把一个点从本来要被感染的状态变成不被感染,那么需要把能把它感染的结点全部删除!!!
对于
对于
1结点来说,0,4能从不同的路径将其感染,即使删除一个,另一个也会将其感染。对于
6节点来说,虽然0,4也能将其感染,但是是从相同路径(要经过4),也就是如果我们删除4,即可避免6被感染!
所以我们要找的就是那些只会被一个结点感染的点(如图中的6),然后存储那个唯一可以感染他的结点,我们采用bfs来完成。如果在bfs过程中遍历到
其他被感染结点则不再遍历下去。
最后我们统计存储的结点中哪个结点出现得最多即可,如果都是0则输出index最小的结点
def minMalwareSpread(self, graph, initial): n = len(graph) d = collections.defaultdict(list) # 对每个初始感染节点依次bfs,因为节点总数不超过300,所以不会超时 for init in initial: vis = set(initial) Q = collections.deque([init]) while Q: infect = Q.popleft() for node in range(len(graph[infect])): if graph[infect][node] == 0: continue if node in vis: continue vis.add(node) d[node].append(init) Q.append(node) # 统计出现最多次的感染节点 res = [0] * n for key in d: if len(d[key]) == 1: res[d[key][0]] += 1 if max(res) == 0: return min(initial) return res.index(max(res))
其实就是渲染每个污染点所在的连通分支,然后观察每个节点被几个污染点污染。对于一个污染点,我们需要找出只被这个污染点污染的个数。然后我们要找出这些数中的最大值。需要注意的是,bfs的过程中,如果遇到另一个污染点,那么就不能将它加入队列中。
def minMalwareSpread(self, graph, initial):
"""
:type graph: List[List[int]]
:type initial: List[int]
:rtype: int
"""
initial.sort()
mi,res=float('inf'),initial[0]
def bfs(target):
cnt=0
vis=[False]*len(graph)
for i in initial:
if vis[i] or i==target: continue
vis[i]=True
cnt+=1
q=[i]
while q:
s=q.pop()
for t in range(len(graph)):
if graph[s][t] and not vis[t] and t!=target:
vis[t]=True
cnt+=1
q.append(t)
return cnt
for i in initial:
t=bfs(i)
# print(i,t)
if t<mi:
mi=t
res=i
return res