LeetCode 920 - Number of Music Playlists

https://leetcode.com/problems/number-of-music-playlists/

Your music player contains N different songs and she wants to listen to L (not necessarily different) songs during your trip.  You create a playlist so that:

• Every song is played at least once
• A song can only be played again only if K other songs have been played

Return the number of possible playlists.  As the answer can be very large, return it modulo 10^9 + 7.

Example 1:

Input: N = 3, L = 3, K = 1
Output: 6
Explanation: There are 6 possible playlists. [1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1].

https://zhanghuimeng.github.io/post/leetcode-920-number-of-music-playlists/

如果用DP来做，第一个问题是状态方程应该包含哪些变量。不妨先把状态方程设置成dp[n][l][k]。然后显然需要思考从哪些状态进行递推这个问题。我觉得之前我总会知道递归的状态的，但现在这好像是一个值得思考的问题。

• dp[n-1][l][k]：比现在少一首歌，但播放列表长度仍然是l。如何把多出来的歌塞进播放列表中是一个问题。
• dp[n][l-1][k]：和现在歌的数量相同，但播放列表长度是l-1。任何在[l-1-k, l-1]位置没有被播放过的歌都可以被再播一遍；而且这一区间内的歌必然是没有重复的。这大概是此题的一个重要性质：合法的播放列表中，任何长度为k的区间内的歌都是互不重复的。很好。所以答案+= dp[n][l-1][k] * (n - k)。
• dp[n][l][k-1]：因为破坏了之前的性质，所以感到很难用这个方法来递推。
• dp[n-1][l-1][k]：比现在少一首歌，播放列表长度也少一首。把新歌插入到播放列表的任何位置都可以（不会缩小任何两首相同的歌之间的间隔），因此答案+= dp[n-1][l-1][k] * (l + 1)。只需把新歌插入到播放列表的最后位置。这首歌可以是任意一首，因此答案+= dp[n-1][l-1][k] * n。[1]

结论是，我们需要考虑的子状态只包括dp[n][l-1][k]和dp[n-1][l-1][k]。由于题目中有N <= L的要求，这一设置是合理的。同时，由于发现根本没有用到k，不妨把k去掉，得到dp[n][l-1]和dp[n-1][l-1]。

以及上面被划掉的部分说明我没有理解清楚此处DP到底意味着什么。DP的状态本身表示什么是很容易说明的：dp[n][l]表示长度为l且有n首不同的歌的播放列表的总数；而dp[n][l] += dp[n-1][l-1][k] * n表示的是，从当前的n首歌里任选一首删除，用n-1首歌组成长度为l-1的播放列表；最后再把选出来的这首歌放在播放列表最后。之所以不是把这首歌插入到播放列表的各个位置，是因为那样就会得到与其他歌重复的状态，因此需要加以限制。

显然上述代码还有很多可以优化的地方，包括但不限于[1]：

• 显然只有j >= i时f[i][j]才有意义。
• 当i == K + 1时，意味着我们只能先播放K + 1首歌曲，然后按相同顺序继续播放同样的歌曲，因此总的可能性数量为i!。
• 当i == j时，歌曲数量和播放列表长度相同，不需要考虑K的问题，因此总的可能性数量也为i!。

https://blog.csdn.net/zjucor/article/details/82956847

思路： 如果先去掉 每首歌必须放一次  这个限制，用DP，dp[i]=dp[i-1]*(n-K)

如果加上这个限制，dp[n][l]表示已经听过了n首歌，一共放了l首歌的总数，dp[n][l]=dp[n-1][l-1]*n+dp[n][l-1]*(n-K)

https://leetcode.com/articles/number-of-music-playlists/
Approach 1: Dynamic Programming

Let dp[i][j] be the number of playlists of length i that have exactly j unique songs. We want dp[L][N], and it seems likely we can develop a recurrence for dp.

Algorithm

Consider dp[i][j]. Last song, we either played a song for the first time or we didn't. If we did, then we had dp[i-1][j-1] * (N-j) ways to choose it. If we didn't, then we repeated a previous song in dp[i-1][j] * max(j-K, 0) ways (j of them, except the last K ones played are banned.)

• Time Complexity: $O(NL)$.
• Space Complexity: $O(NL)$. (However, we can adapt this algorithm to only store the last row of dp to easily get $O(L)$ space complexity.) 

  public int numMusicPlaylists(int N, int L, int K) {

    int MOD = 1_000_000_007;

    long[][] dp = new long[L + 1][N + 1];

    dp[0][0] = 1;

    for (int i = 1; i <= L; ++i)

      for (int j = 1; j <= N; ++j) {

        dp[i][j] += dp[i - 1][j - 1] * (N - j + 1);

        dp[i][j] += dp[i - 1][j] * Math.max(j - K, 0);

        dp[i][j] %= MOD;

      }

    return (int) dp[L][N];

  }

https://leetcode.com/problems/number-of-music-playlists/discuss/180338/DP-solution-that-is-Easy-to-understand

dp[i][j] denotes the solution of i songs with j different songs. So the final answer should be dp[L][N]

Think one step before the last one, there are only cases for the answer of dp[i][j]
case 1 (the last added one is new song): listen i - 1 songs with j - 1 different songs, then the last one is definitely new song with the choices of N - (j - 1).
Case 2 (the last added one is old song): listen i - 1 songs with j different songs, then the last one is definitely old song with the choices of j
if without the constraint of K, the status equation will be
dp[i][j] = dp[i-1][j-1] * (N - (j-1)) + dp[i-1][j] * j

If with the constaint of K, there are also two cases
Case 1: no changes since the last added one is new song. Hence, there is no conflict
Case 2: now we don't have choices of j for the last added old song. It should be updated j - k because k songs can't be chosed from j - 1 to j - k. However, if j <= K, this case will be 0 because only after choosing K different other songs, old song can be chosen.

if (j > k)
dp[i][j] = dp[i-1][j-1] * (N- (j-1)) + dp[i-1][j] * (j-k)
else
dp[i][j] = dp[i-1][j-1] * (N- (j-1))

    public int numMusicPlaylists(int N, int L, int K) {
        int mod = (int)Math.pow(10, 9) + 7;
        long[][] dp = new long[L+1][N+1];
        dp[0][0] = 1;
        for (int i = 1; i <= L; i++){
            for (int j = 1; j <= N; j++){
                dp[i][j] = (dp[i-1][j-1] * (N - (j-1)))%mod; 
                if (j > K){
                    dp[i][j] = (dp[i][j] + (dp[i-1][j] * (j-K))%mod)%mod;
                }
            }
        }
        return (int)dp[L][N];
    }

https://buptwc.github.io/2018/10/08/Leetcode-920-Number-of-Music-Playlists/

这道题一看像一个排列组合问题，熟悉排列组合的人对下面这个式子肯定不陌生

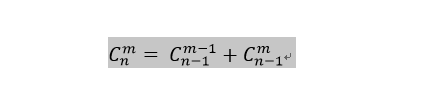
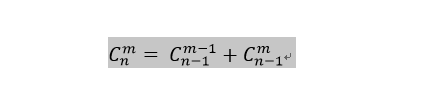
这个式子可以这样描述，在n个人里面挑选m个人，我们从挑不挑得到某个特定人X来考虑。
若挑得到，那么我们从剩下的n-1个人中再挑m-1个人。
若挑不到，那么我们从剩下的n-1个人中挑m个人。

这道题也是用类似的思路，我们定义f(n,l,k)为题目所求，则有：
f(n,l,k) = f(n-1,l-1,k) \* n + f(n,l-1,k) \* (n-k)
其中f(n-1,l-1,k)代表某个特定的歌只最后出现一次，其余n-1首歌填充了前面l-1个位置，因为有n首不同的歌所以乘n。
f(n,l-1,k)代表最后出现的某个特定的歌前面已经出现过了，这个最后出现的歌和当前最后k个位置的歌应当不相同，故乘(n-k)。

递推式已经找到，那么初始状态是什么呢？
显然当n==l时，则就是一个全排列，即为n!
当n > l or k > n时，都不存在解，故为0

注意到在递推式中k其实始终无变化，所以实际定义dp时k可以省去

c(m,n)=c(m-1,n-1)+c(m-1,n)

等式左边表示从m个元素中选取n个元素，而等式右边表示这一个过程的另一种实现方法：任意选择m中的某个备选元素为特殊元素，从m中选n个元素可以由此特殊元素的被包含与否分成两类情况，即n个被选择元素包含了特殊元素和n个被选择元素不包含该特殊元素。前者相当于从m-1个元素中选出n-1个元素的组合，即c(m-1,n-1)；后者相当于从m-1个元素中选出n个元素的组合，即c(m-1,n)。

https://zxi.mytechroad.com/blog/dynamic-programming/leetcode-920-number-of-music-playlists/

dp[i][j] := # of playlists of length i using j different songs.

dp[i][j] = dp[i – 1][j – 1] * (N – (j – 1))  +  // Adding a new song. j – 1 used, choose any one from (N – (j – 1)) unused.
dp[i -1][j] * max(j – K, 0)         // Reuse an existing song.

Time complexity: O(LN)

Space complexity: O(LN) -> O(N)

TODO
https://leetcode.com/articles/number-of-music-playlists/
Approach 2: Partitions + Dynamic Programming

Approach 3: Generating Functions