LeetCode 887 - Super Egg Drop

https://leetcode.com/problems/super-egg-drop/

You are given K eggs, and you have access to a building with N floors from 1 to N. 

Each egg is identical in function, and if an egg breaks, you cannot drop it again.

You know that there exists a floor F with 0 <= F <= N such that any egg dropped at a floor higher than F will break, and any egg dropped at or below floor F will not break.

Each move, you may take an egg (if you have an unbroken one) and drop it from any floor X (with 1 <= X <= N). 

Your goal is to know with certainty what the value of F is.

What is the minimum number of moves that you need to know with certainty what F is, regardless of the initial value of F?

Example 1:

Input: K = 1, N = 2
Output: 2
Explanation: 
Drop the egg from floor 1.  If it breaks, we know with certainty that F = 0.
Otherwise, drop the egg from floor 2.  If it breaks, we know with certainty that F = 1.
If it didn't break, then we know with certainty F = 2.
Hence, we needed 2 moves in the worst case to know what F is with certainty.

Example 2:

Input: K = 2, N = 6
Output: 3

X.

https://leetcode.com/problems/super-egg-drop/discuss/159055/Java-DP-solution-from-O(KN2)-to-O(KNlogN)
We can easily come up with an O(KN^2) DP solution, where dp[k][n] = min(1 + max(dp[k - 1][i - 1], dp[k][n - i])) i = 1...n
In this implementation, we use recursion to simulate each move.

    public int superEggDrop(int K, int N) {
        int[][] memo = new int[K + 1][N + 1];
        return helper(K, N, memo);
    }
    private int helper(int K, int N, int[][] memo) {
        if (N <= 1) {
            return N;
        }
        if (K == 1) {
            return N;
        }
        if (memo[K][N] > 0) {
            return memo[K][N];
        }
        int min = N;
        for (int i = 1; i <= N; i++) {
            int left = helper(K - 1, i - 1, memo);
            int right = helper(K, N - i, memo);
            min = Math.min(min, Math.max(left, right) + 1);
        }
        memo[K][N] = min;
        return min;
    }

https://www.cnblogs.com/Phantom01/p/9490508.html

O(K * N^2)
首先，这个题比较绕。需要求一个最优决策使得步数最小，但是实际的步数是随着真实结果变化而变化的。
于是，为了保证在我们假设的步数内一定能够解完，我们可以假设每次决策都会得到最坏结果。

dp[n][k] 表示用k个鸡蛋测n层最少需要多少步。
我们可以枚举第一次在第i层扔鸡蛋，会得到两种结果:

1. 鸡蛋坏掉: 我们接下来需要面对的情形是: 用 k-1 个鸡蛋来测量 i-1 层，所以最少需要 dp[i-1][k-1] 步。
2. 鸡蛋没坏: 我们接下来要面对的情形是: 用 k 个鸡蛋来测量 n-i 层，所以最少需要 dp[n-i][k] 步。
   因为我们总会面对最坏情况，所以，在第i层扔，会用 max(dp[i-1][k-1], dp[n-i][k]) + 1 步。

所以我们的递推式如下:
dp[n][k] = min{ max(dp[i-1][k-1], dp[n-i][k]) + 1 } (1 <= i <= n)

int superEggDrop(int K, int N) {
    int dp[MAXN+2][MAXK+2];
    for (int i = 0; i <= MAXN; i++) {
        dp[i][0] = 0;
        dp[i][1] = i;
    }
    for (int j = 2; j <= MAXK; j++) {
        for (int i = 1; i <= MAXN; i++) {
            dp[i][j] = i;
            for (int k = 1; k < i; k++) {
                dp[i][j] = min(dp[i][j], max(dp[k-1][j-1], dp[i-k][j]) + 1);
            }
        }
    }
    return dp[N][K];
}

https://blog.csdn.net/XX_123_1_RJ/article/details/82284902
（1）先考虑原问题：100层楼，2个鸡蛋的情况。 
（2）设dp[n]表示从第n层丢下鸡蛋，没有摔碎的最少操作次数。先给出dp方程式为：

dp[n] = min(1 + max(i-1, dp[n-i]))   其中：(i in [1, n])  # dp[n]通过遍历之前的值得到。
dp[1] = 1
1
2
   解释： 
   假设：第一个鸡蛋从第i层扔下来。那么有两个情况。 
   A： 碎了，第二个鸡蛋只能从第 1 层，依次向上试，共有操作i - 1次。 
   B： 没碎，两个鸡蛋还都健在，楼上还有 n - i层，此时的问题，就转换成本问题的，子问题了dp[n-i]。 
   C： 所以 max(i-1, dp[n-i]) 表示两种情况最差的一种，也就是操作次数最多的哪一种。 
   D： 1 + max(i-1, dp[n-i])，前面那个 1可以理解为本次操作。 
   E： 最后，很显然，我们不知道 最优的 i 层 在哪里对吧？所以通过 枚举 或者 遍历 选出来。也就是上面的状态转换方程了。 
（3）现在看看本题，N层楼，K个鸡蛋的情况。 
   A： 设 dp[n][k] 为，n 层楼，k 个鸡蛋找到 F的最少操作次数。 
   B： 当第一个鸡蛋从第 i 层丢下， 
   C： 碎了，那么现在剩下 k - 1 个鸡蛋，此时说明 F 在楼下（i 层的下面），接下来还要进行操作 dp[i-1][k-1] 次（子问题）； 
   D： 如果没碎，说明此时的 F 在楼上（i 层的上面），接下来还要操作dp[n-i][k] 次（子问题哦）。 
所以得出dp方程：

dp[n][k] = min(1 + max(dp[i-1][k-1], dp[n-i][k]))  其中：(i in [1, n])
dp[i][1] = i
1
2
做到这里，本以为可以AC了，遗憾的是，这种方式基本是对所有情况的检测，有点暴力，所以TLE（也可能是用Python3的缘故，Python2就可以顺利通过）。 
（4）继续学习，换个思维方式，再做一次。 
   A： 设 dp[m][k] 为，k 个鸡蛋， m次操作（扔m次），可以判定的最大楼层数。现在的dp 方程如下：

dp[m][k] = dp[m - 1][k] + dp[m - 1][k - 1] + 1
1
   B： 如果当前鸡蛋 - 碎了， 此时，能判断出的楼层数，最少为 dp[m - 1][k - 1] 
   C： 如果当前鸡蛋 - 没碎，此时，能判断出的楼层数，最多为 dp[m - 1][ k ] ，现在是不是还有 k个鸡蛋？而这k 个鸡蛋是不是 至少又可以向上 判断出 dp[m - 1][k - 1] 层，（因为之前已经算过了，只要加上就可以了。） 然后在加上当前这 1 层。所以总体就是上面的方程式了。 
—–（不知道，这种理解是否正确或者严谨，大神可以指点哦。） 
   D： dp[m][k] 类似于组合的数量，并且它以指数方式增加到N， 还有一种理解方法，就是可以联想，上台阶问题（也不太严谨哈）。

再分析一个小栗子，假设只有 2 个鸡蛋，至少 扔鸡蛋 X 次，可以判断出100层楼。

很显然，第一个鸡蛋要从X层扔下去，如果烂了，还可以用另外一个鸡蛋从第一层向上开始扔。 
现在，希望至少 扔鸡蛋 X 次，就可以判断出100层楼。那就假设鸡蛋一直没烂，第一次扔完鸡蛋之后，可以得出楼层 X，然后还有X-1次机会，第二扔完又没烂，然后还有X-2次机会，这样一推理，可以得到的楼层数为： X + (X - 1) + (X - 2) + … + 1 = X(X+1) / 2 >=100，解方程，求出X，即可。感觉这个例子可以帮助理解上面那个公式：dp[m][k] = dp[m - 1][k] + dp[m - 1][k - 1] + 1。参加链接[1]

http://tashi711.xyz/programming/reports/leetcode/leetcode-887/

很容易想到一个暴力的DP，O(KN2)$O(K{N}^2)$。也就是


dp(k,n)=min1≤x≤n{dp(k−1,x−1),dp(k,x−k)}$$dp(k,n)=\underset{1\le x\le n}{min}\{dp(k-1,x-1),dp(k,x-k)\}$$
　　虽然超时，但是我们能发现min项里面前者随着x增大而增大，后者随着x增大而减小，因此使用二分查找就可以找到恰当的x，复杂度可以被优化到O(KNlogN)$O(KN\log N)$，已经可以满足解决这道问题了。进一步想想还可以做优化，dp项随着n增大，取到最优的x也会随着增大，因此其实可以寻找当前x时从上个阶段最优的x开始，而不是从1开始，这样均摊复杂度就只有O(KN)$O(KN)$了。
　　官方题解还给出了更加优化的算法可以达到O(KlogN)$O(K\log N)$，有兴趣可以去看下，不过需要用到一些组合数学的推理，难度比较大，整体思想比较巧妙，他假设了另外一个问题，给定T次移动和K个鸡蛋，能够达到最大的层数f(T, K)是多少，于是问题变为找到最小的T使得f(T, K)≥N，而T又是可以二分查找的



https://zhanghuimeng.github.io/post/leetcode-887-super-egg-drop/


比赛的时候我好像尝试这样推导了一下：以两个鸡蛋的情况为例，如果进行二分式的扔法，就会出现这样的情形：

从N/2处丢下鸡蛋，鸡蛋碎了，于是之后只能从下往上逐层丢鸡蛋，需要约N/2次操作
从N/2处丢下鸡蛋，鸡蛋没碎，于是可以把这个鸡蛋再次从3/4*N层丢下去

如果鸡蛋碎了，则之后需要从N/2+1到3/4*N-1逐层丢鸡蛋，需要约N/4次操作
如果鸡蛋没碎，则可以把这个鸡蛋再次从7/8*N层丢下去
……




可以看出，鸡蛋碎了的情况需要的迭代次数比较多，所以不应该二分，而应该偏分，鸡蛋可能碎掉的情况分配的层数少一点……比如三分？

想到这里比赛就结束了……

X. DP with binaray search

https://github.com/just4once/leetcode/blob/master/leetcode/binary-search/887-super-egg-drop.md


Brute Force with DP (TLE)

We create an dp array to store the best moves for each eggs and floors combination, where dp[i][j] represents the moves for i eggs and j floors
For current eggs and floors, the best moves is obtained by dropping the egg from 1st floor up to current floor
The minimum of all these drop tests are our answer
For each test on ith floor, ranges from 1 to current floor, the egg could either break, so we need to use less egg on remaining floor dp[curEgg - 1][i - 1], or it doesn't, so we use dp[curEgg][curFloor - i]
Because we are expecting worst case, the maximum of them + 1 (current egg drop) is the answer for dropping at ith floor
Time complexity O(KN^2)
Space complexity O(KN)


DP with Binary

Notice the function dp( K - 1, i - 1) increases when i increase, while on the other hand, dp(K, N - i) decreases when i increase
We can use this observation to speed up the search for minimum i
Time complexity O(KNlogN)
Space complexity O(KN)









X. 思路: O(K * logN)


X. 

2004 - 朱晨光：《优化，再优化！——从《鹰蛋》一题浅析对动态规划算法的优化》/朱晨光.pdf

The 5th algorithm in this paper includes an even more detailed explanation of this solution (Chinese edition), and the time complexity should be O(n ^ 1/2) with a simple special handling logic for the K = 1 case.

https://leetcode.com/problems/super-egg-drop/discuss/158974/C%2B%2BJavaPython-2D-and-1D-DP-O(KlogN)

Drop eggs is a very classical problem.
Some people may come up with idea O(KN^2)
where dp[K][N] = 1 + max(dp[K - 1][i - 1],dp[K][N - i]) for i in 1...N.
However this idea is very brute force, for the reason that you check all possiblity.



So I consider this problem in a different way:
dp[M][K]means that, given K eggs and M moves,
what is the maximum number of floor that we can check.



The dp equation is:
dp[m][k] = dp[m - 1][k - 1] + dp[m - 1][k] + 1,
which means we take 1 move to a floor,
if egg breaks, then we can check dp[m - 1][k - 1] floors.
if egg doesn't breaks, then we can check dp[m - 1][k] floors.



dp[m][k] is similar to the number of combinations and it increase exponentially to N




    public int superEggDrop(int K, int N) {
        int[][] dp = new int[N + 1][K + 1];
        int m = 0;
        while (dp[m][K] < N) {
            ++m;
            for (int k = 1; k <= K; ++k)
                dp[m][k] = dp[m - 1][k - 1] + dp[m - 1][k] + 1;
        }
        return m;
    }





    public int superEggDrop(int K, int N) {
        int dp[] = new int[K + 1], m = 0;
        for (m = 0; dp[K] < N; ++m)
            for (int k = K; k > 0; --k)
                dp[k] += dp[k - 1] + 1;
        return m;
    }


https://leetcode.com/problems/super-egg-drop/discuss/159508/easy-to-understand

firstly, if we have k eggs and s steps to detect a building with Q(k, s) floors, 

secondly, we use 1 egg and 1 step to detect one floor, 
if egg break, we can use (k-1) eggs and (s-1) to detect with Q(k-1, s-1), 
if egg isn't broken, we can use k eggs and (s-1) step to detech with Q(k, s-1),
So, Q(k, s) = 1 + Q(k, s-1) + Q(k-1, s-1);

dp[i] is max floors we can use i eggs and s step to detect.


public:
    int superEggDrop(int K, int N) {
        vector<int> dp(K+1);
        int step = 0;
        for (; dp[K] < N; step++) {
            for (int i = K; i > 0; i--)
                dp[i] = (1 + dp[i] + dp[i-1]);
        }
        return step;
    }


我们可以改变一下求解的思路，求k个鸡蛋在m步内可以测出多少层：

假设: dp[k][m] 表示k个鸡蛋在m步内最多能测出的层数。
那么，问题可以转化为当 k <= K 时，找一个最小的m，使得dp[k][m] <= N。

我们来考虑下求解dp[k][m]的策略：
假设我们有k个鸡蛋第m步时，在第X层扔鸡蛋。这时候，会有两种结果，鸡蛋碎了，或者没碎。
如果鸡蛋没碎，我们接下来会在更高的楼层扔，最多能确定 X + dp[k][m-1] 层的结果；
如果鸡蛋碎了，我们接下来会在更低的楼层扔，最多能确定 Y + dp[k-1][m-1] 层的结果 (假设在第X层上还有Y层)。
因此，这次扔鸡蛋，我们最多能测出 dp[k-1][m-1] (摔碎时能确定的层数) + dp[k][m-1] (没摔碎时能确定的层数) + 1 (本层) 层的结果。
另外，我们知道一个鸡蛋一次只能测一层，没有鸡蛋一层都不能测出来。
因此我们可以列出完整的递推式:
dp[k][0] = 0
dp[1][m] = m (m > 0)
dp[k][m] = dp[k-1][m-1] + dp[k][m-1] + 1 (k > 0, m>0)

// NOTE: 第一维和第二维换了下位置
int superEggDrop(int K, int N) {
    int dp[N+2][K+2];
    memset(dp, 0, sizeof(dp));
    dp[0][0] = 0;
    for (int m = 1; m <= N; m++) {
        dp[m][0] = 0;
        for (int k = 1; k <= K; k++) {
            dp[m][k] = dp[m-1][k] + dp[m-1][k-1] + 1;
            if (dp[m][k] >= N) {
                return m;
            }
        }
    }
    return N;
}

X. https://leetcode.com/problems/super-egg-drop/discuss/158974/C%2B%2BJavaPython-2D-and-1D-DP-O(KlogN)

Drop eggs is a very classical problem.
Some people may come up with idea O(KN^2)
where dp[K][N] = 1 + max(dp[K - 1][i - 1],dp[K][N - i]) for i in 1...N.
However this idea is very brute force, for the reason that you check all possiblity.

So I consider this problem in a different way:
dp[M][K]means that, given K eggs and M moves,
what is the maximum number of floor that we can check.

The dp equation is:
dp[m][k] = dp[m - 1][k - 1] + dp[m - 1][k] + 1,
which means we take 1 move to a floor,
if egg breaks, then we can check dp[m - 1][k - 1] floors.
if egg doesn't breaks, then we can check dp[m - 1][k - 1] floors.

dp[m][k] is similar to the number of combinations and it increase exponentially to N

    public int superEggDrop(int K, int N) {
        int[][] dp = new int[N + 1][K + 1];
        int m = 0;
        while (dp[m][K] < N) {
            ++m;
            for (int k = 1; k <= K; ++k)
                dp[m][k] = dp[m - 1][k - 1] + dp[m - 1][k] + 1;
        }
        return m;
    }

C++/Java O(KlogN) Time, O(K) Space

    public int superEggDrop(int K, int N) {
        int dp[] = new int[K + 1], m = 0;
        for (m = 0; dp[K] < N; ++m)
            for (int k = K; k > 0; --k)
                dp[k] += dp[k - 1] + 1;
        return m;
    }




X.
https://leetcode.com/problems/super-egg-drop/discuss/159055/Java-DP-solution-from-O(KN2)-to-O(KNlogN)

Notice that for the same K when N goes up, dp[K][N] goes up.
Then for int left = helper(K - 1, i - 1, memo); int right = helper(K, N - i, memo); when i goes up, left goes up and right goes down.
We can use Binary Search here to get the minimum Math.max(left, right) + 1, when left and right are as close as possible.
We come to this O(KNlogN) solution:

    public int superEggDrop(int K, int N) {
        int[][] memo = new int[K + 1][N + 1];
        return helper(K, N, memo);
    }
    private int helper(int K, int N, int[][] memo) {
        if (N <= 1) {
            return N;
        }
        if (K == 1) {
            return N;
        }
        if (memo[K][N] > 0) {
            return memo[K][N];
        }
        
        int low = 1, high = N, result = N;
        while (low < high) {
            int mid = low + (high - low) / 2;
            int left = helper(K - 1, mid - 1, memo);
            int right = helper(K, N - mid, memo);
            result = Math.min(result, Math.max(left, right) + 1);
            if (left == right) {
                break;
            } else if (left < right) {
                low = mid + 1;
            } else {
                high = mid;
            }
        }
        memo[K][N] = result;
        return result;
    }




Approach 1: Dynamic Programming with Binary Search

It's natural to attempt dynamic programming, as we encounter similar subproblems. Our state is (K, N): Keggs and N floors left. When we drop an egg from floor X, it either survives and we have state (K, N-X), or it breaks and we have state (K-1, X-1).

This approach would lead to a $O(K N^2)$ algorithm, but this is not efficient enough for the given constraints. However, we can try to speed it up. Let dp(K, N) be the maximum number of moves needed to solve the problem in state (K, N). Then, by our reasoning above, we have:

$\text{dp}(K, N) = \min\limits_{1 \leq X \leq N} \Big( \max(\text{dp}(K-1, X-1), \text{dp}(K, N-X)) \Big)$

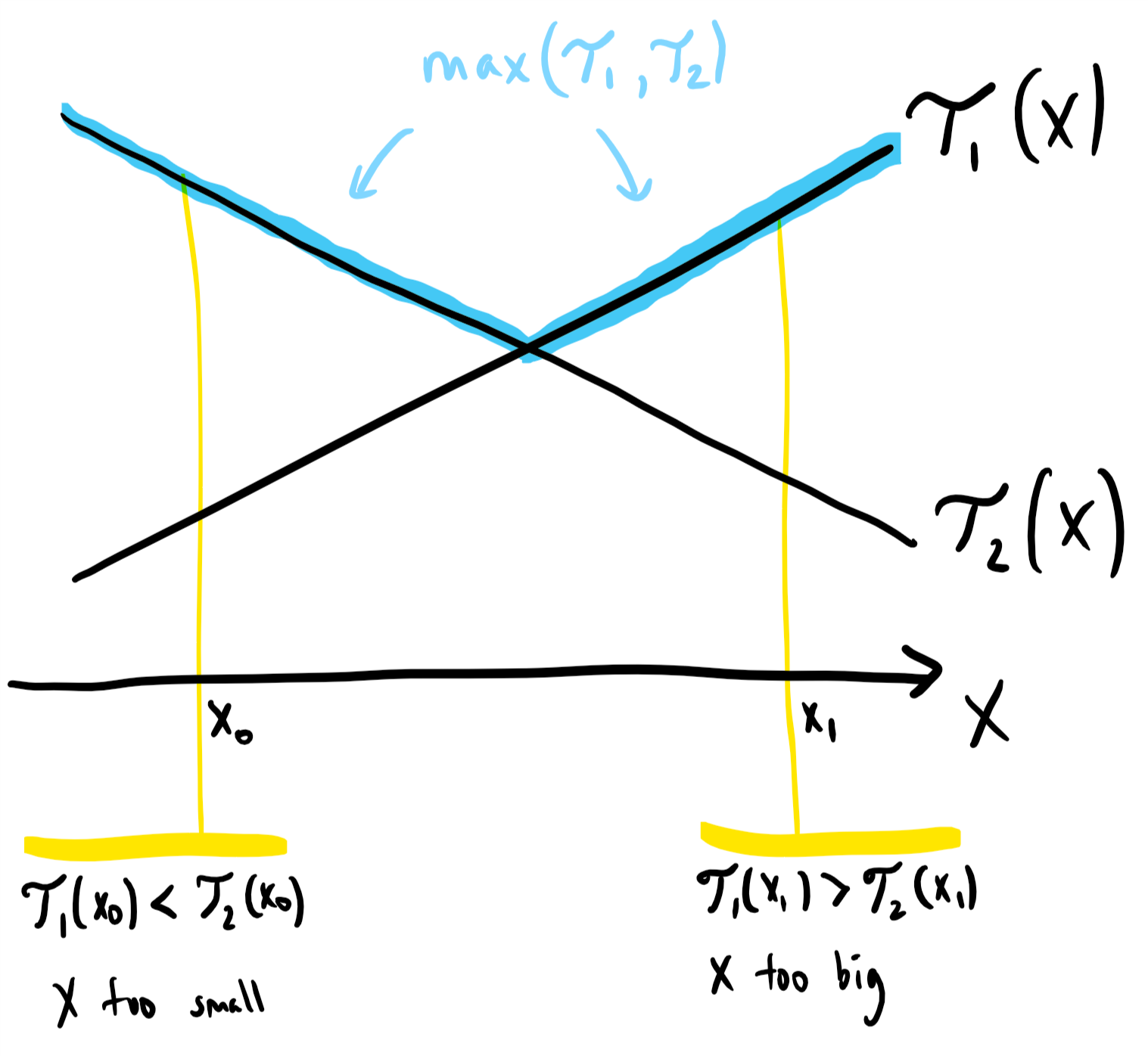
Now for the key insight: Because $\text{dp}(K, N)$ is a function that is increasing on $N$, the first term $\mathcal{T_1} = \text{dp}(K-1, X-1)$ in our $\max$ expression is an increasing function on $X$, and the second term $\mathcal{T_2} = \text{dp}(K, N-X)$ is a decreasing function on $X$. This means that we do not need to check every $X$ to find the minimum -- instead, we can binary search for the best $X$.

Algorithm

Continuing our discussion, if $\mathcal{T_1} < \mathcal{T_2}$, then the $X$ value chosen is too small; and if $\mathcal{T_1} > \mathcal{T_2}$, then $X$ is too big. However, this argument is not quite correct: when there are only two possible values of $X$, we need to check both.

Using the above fact, we can use a binary search to find the correct value of $X$ more efficiently than checking all $N$ of them.

• Time Complexity: $O(K * N \log N)$.
• Space Complexity: $O(K * N)$. 

  public int superEggDrop(int K, int N) {

    return dp(K, N);

  }

  Map<Integer, Integer> memo = new HashMap();

  public int dp(int K, int N) {

    if (!memo.containsKey(N * 100 + K)) {

      int ans;

      if (N == 0)

        ans = 0;

      else if (K == 1)

        ans = N;

      else {

        int lo = 1, hi = N;

        while (lo + 1 < hi) {

          int x = (lo + hi) / 2;

          int t1 = dp(K - 1, x - 1);

          int t2 = dp(K, N - x);

          if (t1 < t2)

            lo = x;

          else if (t1 > t2)

            hi = x;

          else

            lo = hi = x;

        }

        ans = 1 + Math.min(Math.max(dp(K - 1, lo - 1), dp(K, N - lo)), Math.max(dp(K - 1, hi - 1), dp(K, N - hi)));

      }

      memo.put(N * 100 + K, ans);

    }

    return memo.get(N * 100 + K);

  }

Approach 2: Dynamic Programming with Optimality Criterion

As in Approach 1, we try to speed up our $O(K N^2)$ algorithm. Again, for a state of $K$ eggs and $N$ floors, where $\text{dp}(K, N)$ is the answer for that state, we have:

$\text{dp}(K, N) = \min\limits_{1 \leq X \leq N} \Big( \max(\text{dp}(K-1, X-1), \text{dp}(K, N-X)) \Big)$

Now, suppose $X_{\emptyset} = \text{opt}(K, N)$ is the smallest $X$ for which that minimum is attained: that is, the smallest value for which

$\text{dp}(K, N) = \Big( \max(\text{dp}(K-1, X_{\emptyset}-1), \text{dp}(K, N-X_{\emptyset})) \Big)$

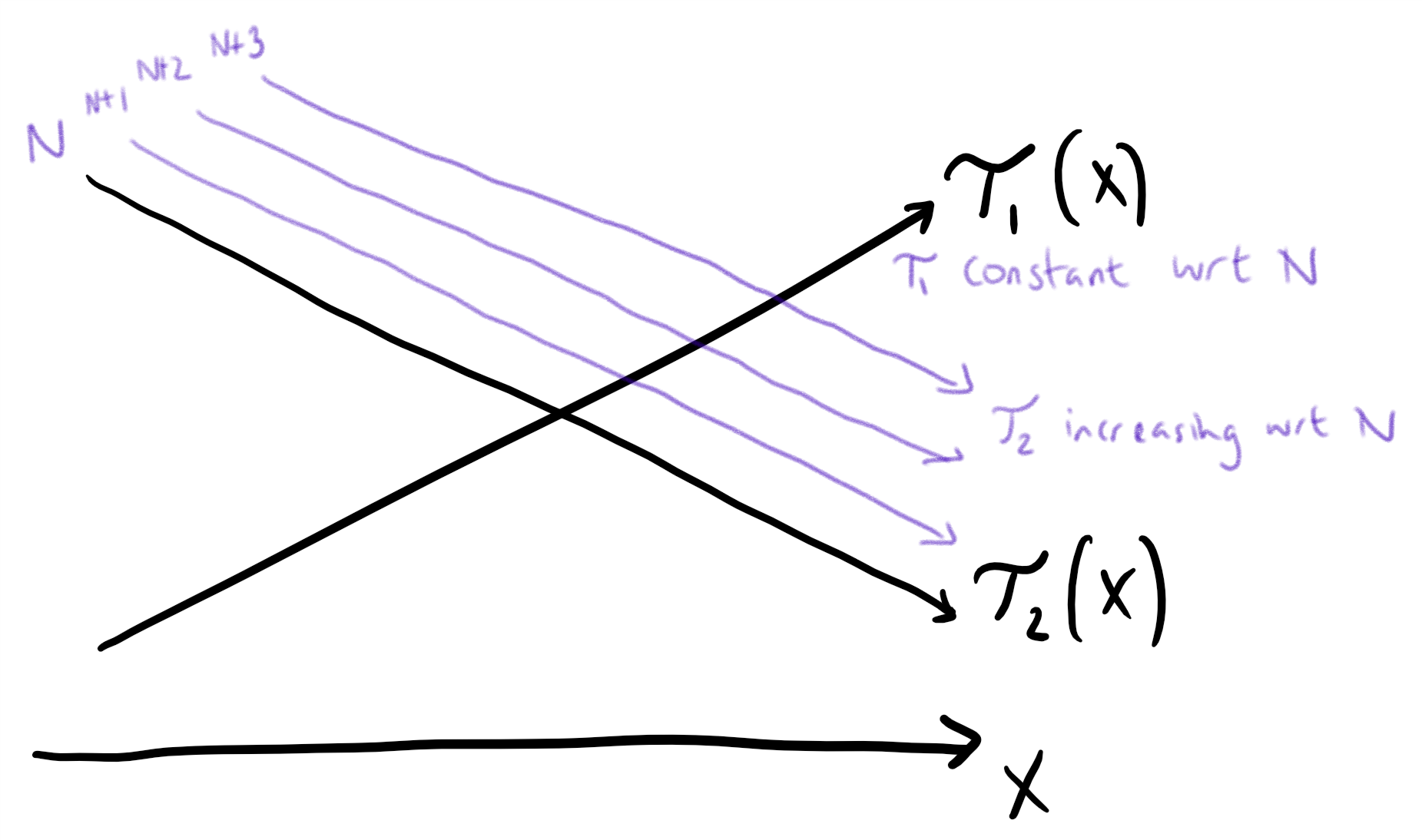
The key insight that we will develop below, is that $\text{opt}(K, N)$ is an increasing function in $N$.

The first term of our $\max$ expression, $\mathcal{T_1} = \text{dp}(K-1, X-1)$, is increasing with respect to $X$, but constant with respect to $N$. The second term, $\mathcal{T_2} = \text{dp}(K, N-X)$, is decreasing with respect to $X$, but increasing with respect to $N$.

This means that as $N$ increases, the intersection point $X_{\emptyset} = \text{opt}(K, N)$ of these two lines is increasing, as we can see in the diagram.

Algorithm

Perform "bottom up" dynamic programming based on the recurrence below, keeping track of $X_{\emptyset} = \text{opt}(K, N)$. Again:

$\text{dp}(K, N) = \min\limits_{1 \leq X \leq N} \Big( \max(\text{dp}(K-1, X-1), \text{dp}(K, N-X)) \Big)$

When we want to find $\text{dp}(K, N+1)$, instead of searching for $X$ from $1 \leq X \leq N$, we only have to search through $X_{\emptyset} \leq X \leq N$.

Actually, (as illustrated by the diagram,) if ever the next $X+1$ is worse than the current $X$, then we've searched too far, and we know our current $X$ is best for this $N$.

  public int superEggDrop(int K, int N) {

    // Right now, dp[i] represents dp(1, i)

    int[] dp = new int[N + 1];

    for (int i = 0; i <= N; ++i)

      dp[i] = i;

    for (int k = 2; k <= K; ++k) {

      // Now, we will develop dp2[i] = dp(k, i)

      int[] dp2 = new int[N + 1];

      int x = 1;

      for (int n = 1; n <= N; ++n) {

        // Let's find dp2[n] = dp(k, n)

        // Increase our optimal x while we can make our answer better.

        // Notice max(dp[x-1], dp2[n-x]) > max(dp[x], dp2[n-x-1])

        // is simply max(T1(x-1), T2(x-1)) > max(T1(x), T2(x)).

        while (x < n && Math.max(dp[x - 1], dp2[n - x]) > Math.max(dp[x], dp2[n - x - 1]))

          x++;

        // The final answer happens at this x.

        dp2[n] = 1 + Math.max(dp[x - 1], dp2[n - x]);

      }

      dp = dp2;

    }

    return dp[N];

  }

Approach 3: Mathematical

Let's ask the question in reverse: given $T$ moves (and $K$ eggs), what is the most number of floors $f(T, K)$that we can still "solve" (find $0 \leq F \leq f(T, K)$ with certainty)? Then, the problem is to find the least $T$ for which $f(T, K) \geq N$. Because more tries is always at least as good, $f$ is increasing on $T$, which means we could binary search for the answer.

Now, we find a similar recurrence for $f$ as in the other approaches. If in an optimal strategy we drop the egg from floor $X_{\emptyset}$, then either it breaks and we can solve $f(T-1, K-1)$ lower floors (floors $< X_{\emptyset}$); or it doesn't break and we can solve $f(T-1, K)$ higher floors (floors $\geq X_{\emptyset}$). In total,

$f(T, K) = 1 + f(T-1, K-1) + f(T-1, K)$

Also, it is easily seen that $f(t, 1) = t$ when $t \geq 1$, and $f(1, k) = 1$ when $k \geq 1$.

From here, we don't need to solve the recurrence mathematically - we could simply use it to generate all $O(K * \max(T))$ possible values of $f(T, K)$.

However, there is a mathematical solution to this recurrence. If $g(t, k) = f(t, k) - f(t, k-1)$, [the difference between the $k-1$th and $k$th term,] then subtracting the two equations:

$f(T, K) = 1 + f(T-1, K-1) + f(T-1, K)$

$f(T, K-1) = 1 + f(T-1, K-2) + f(T-1, K-1)$

we get:

$g(t, k) = g(t-1, k) + g(t-1, k-1)$

This is a binomial recurrence with solution $g(t, k) = \binom{t}{k+1}$, so that indeed,

$f(t, k) = \sum\limits_{1 \leq x \leq K} g(t, x) = \sum \binom{t}{x}$

Alternative Mathematical Derivation

Alternatively, when we have $t$ tries and $K$ eggs, the result of our $t$ throws must be a $t$-length sequence of successful and failed throws, with at most K failed throws. The number of sequences with $0$ failed throws is $\binom{t}{0}$, the number of sequences with $1$ failed throw is $\binom{t}{1}$ etc., so that the number of such sequences is $\sum\limits_{0 \leq x \leq K} \binom{t}{x}$.

Hence, we can only distinguish at most these many floors in $t$ tries (as each sequence can only map to 1 answer per sequence.) This process includes distinguishing $F = 0$, so that the corresponding value of $N$ is one less than this sum.

However, this is also a lower bound for the number of floors that can be distinguished, as the result of a throw on floor $X$ will bound the answer to be either at most $X$ or greater than $X$. Hence, in an optimal throwing strategy, each such sequence actually maps to a unique answer.

Algorithm

Recapping our algorithm, we have the increasing [wrt $t$] function $f(t, K) = \sum\limits_{1 \leq x \leq K} \binom{t}{x}$, and we want the least $t$ so that $f(t, K) \geq N$. We binary search for the correct $t$.

To evaluate $f(t, K)$ quickly, we can transform the previous binomial coefficient to the next (in the summand) by the formula $\binom{n}{k} * \frac{n-k}{k+1} = \binom{n}{k+1}$.

Time Complexity: $O(K * \log N)$.

  public int superEggDrop(int K, int N) {

    int lo = 1, hi = N;

    while (lo < hi) {

      int mi = (lo + hi) / 2;

      if (f(mi, K, N) < N)

        lo = mi + 1;

      else

        hi = mi;

    }

    return lo;

  }

  public int f(int x, int K, int N) {

    int ans = 0, r = 1;

    for (int i = 1; i <= K; ++i) {

      r *= x - i + 1;

      r /= i;

      ans += r;

      if (ans >= N)

        break;

    }

    return ans;

  }