LeetCode 934 - Shortest Bridge

https://leetcode.com/problems/shortest-bridge/

In a given 2D binary array A, there are two islands.  (An island is a 4-directionally connected group of 1s not connected to any other 1s.)

Now, we may change 0s to 1s so as to connect the two islands together to form 1 island.

Return the smallest number of 0s that must be flipped.  (It is guaranteed that the answer is at least 1.)

Example 1:

Input: [[0,1],[1,0]]
Output: 1

Example 2:

Input: [[0,1,0],[0,0,0],[0,0,1]]
Output: 2

https://leetcode.com/problems/shortest-bridge/discuss/189293/C%2B%2B-BFS-Island-Expansion-%2B-UF-Bonus
We first paint one of the islands using DFS with color 2, so we can easily identify island #1 and island #2. Thanks @davidluoyes for pointing out that we only need to paint one island.

Then we start expanding island #2 by paining connected empty area. Each round, we increase the color (3, 4, and so on) so we can keep track of the newly painted area. This ends when we "bump" into the first island.

The fact that we are increasing the color is also useful for the backtracking, if we need to return the coordinates of the bridge.

int paint(vector<vector<int>>& A, int i, int j) {
    if (i < 0 || j < 0 || i == A.size() || j == A.size() || A[i][j] != 1) return 0;
    A[i][j] = 2;
    return 1 + paint(A, i + 1, j) + paint(A, i - 1, j) + paint(A, i, j + 1) + paint(A, i, j - 1);
}
bool expand(vector<vector<int>>& A, int i, int j, int cl) {
    if (i < 0 || j < 0 || i == A.size() || j == A.size()) return false;
    if (A[i][j] == 0) A[i][j] = cl + 1;
    return A[i][j] == 1;
}  
int shortestBridge(vector<vector<int>>& A) {
    for (int i = 0, found = 0; !found && i < A.size(); ++i)
        for (int j = 0; !found && j < A[0].size(); ++j) found = paint(A, i, j);
    
    for (int cl = 2; ; ++cl)
        for (int i = 0; i < A.size(); ++i)
            for (int j = 0; j < A.size(); ++j) 
                if (A[i][j] == cl && ((expand(A, i - 1, j, cl) || expand(A, i, j - 1, cl) || 
                    expand(A, i + 1, j, cl) || expand(A, i, j + 1, cl))))
                        return cl - 2;
}

As a bonus, below is the union-find based solution. We convert the map into the graph, and join connected "land" cells into sub-graphs (island #1 and island #2). Then, we expand both of these islands by adding directly connected "water" cells to the sub-graphs. Finally, we stop when we detect that two sub-graphs are about to merge into one.

Interestingly, the runtime of these two very different solutions are similar (24 - 35 ms), and the UF solution is much more complex. Probably, the UF solution can be further optimized by only processing direct connections...

int uf_find(int i, vector<int>& nodes) {
  if (nodes[i] <= 0) return i;
  else return nodes[i] = uf_find(nodes[i], nodes);
}
int uf_union(int i, int j, vector<int>& nodes) {
  auto pi = uf_find(i, nodes), pj = uf_find(j, nodes);
  if (pi == pj) return 0;
  if (nodes[pi] > nodes[pj]) swap(pi, pj);
  nodes[pi] += min(-1, nodes[pj]);
  nodes[pj] = pi;
  return -nodes[pi];
}
int shortestBridge(vector<vector<int>> &A) {
  int sz = A.size();
  vector<int> nodes(sz * sz + 1);
  list<pair<int, int>> edges;
  for (auto i = 0; i < sz; ++i)
    for (auto j = 0; j < sz; ++j) {
      auto idx = i * sz + j + 1;
      if (A[i][j]) nodes[idx] = -1;
      if (j > 0) {
        if (A[i][j] && A[i][j - 1]) uf_union(idx - 1, idx, nodes);
        else edges.push_back({ idx - 1, idx });
      }
      if (i > 0) {
        if (A[i][j] && A[i - 1][j]) uf_union(idx - sz, idx, nodes);
        else edges.push_back({ idx - sz, idx });
      }
    }

  for (auto step = 1; ; ++step) {
    vector<pair<int, int>> merge_list;
    for (auto it = edges.begin(); it != edges.end(); ) {
      if (nodes[it->first] == 0 && nodes[it->second] == 0) ++it;
      else {
        if (nodes[it->first] != 0 && nodes[it->second] != 0) {
          if (uf_find(it->first, nodes) != uf_find(it->second, nodes)) return (step - 1) * 2;
        }
        merge_list.push_back({ it->first, it->second });
        edges.erase(it++);
      }
    }
    for (auto p : merge_list) {
      if (nodes[p.first] != 0 && nodes[p.second] != 0) {
        if (uf_find(p.first, nodes) != uf_find(p.second, nodes)) return step * 2 - 1;
      }
      uf_union(p.first, p.second, nodes);
    }
  }
}

https://leetcode.com/problems/shortest-bridge/discuss/189315/Java-DFS%2BBFS-traverse-the-2D-array-once
https://leetcode.com/problems/shortest-bridge/discuss/189321/Java-DFS-find-the-island-greater-BFS-expand-the-island

    public int shortestBridge(int[][] A) {
        int m = A.length, n = A[0].length;
        boolean[][] visited = new boolean[m][n];
        int[][] dirs = new int[][]{{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
        Queue<int[]> q = new LinkedList<>();
        boolean found = false;
        // 1. dfs to find an island, mark it in `visited`
        for (int i = 0; i < m; i++) {
            if (found) {
                break;
            }
            for (int j = 0; j < n; j++) {
                if (A[i][j] == 1) {
                    dfs(A, visited, q, i, j, dirs);
                    found = true;
                    break;
                }
            }
        }
        // 2. bfs to expand this island
        int step = 0;
        while (!q.isEmpty()) {
            int size = q.size();
            while (size-- > 0) {
                int[] cur = q.poll();
                for (int[] dir : dirs) {
                    int i = cur[0] + dir[0];
                    int j = cur[1] + dir[1];
                    if (i >= 0 && j >= 0 && i < m && j < n && !visited[i][j]) {
                        if (A[i][j] == 1) {
                            return step;
                        }
                        q.offer(new int[]{i, j});
                        visited[i][j] = true;
                    }
                }
            }
            step++;
        }
        return -1;
    }
    private void dfs(int[][] A, boolean[][] visited, Queue<int[]> q, int i, int j, int[][] dirs) {
        if (i < 0 || j < 0 || i >= A.length || j >= A[0].length || visited[i][j] || A[i][j] == 0) {
            return;
        }
        visited[i][j] = true;
        q.offer(new int[]{i, j});
        for (int[] dir : dirs) {
            dfs(A, visited, q, i + dir[0], j + dir[1], dirs);
        }
    }

Approach 1: Find and Grow

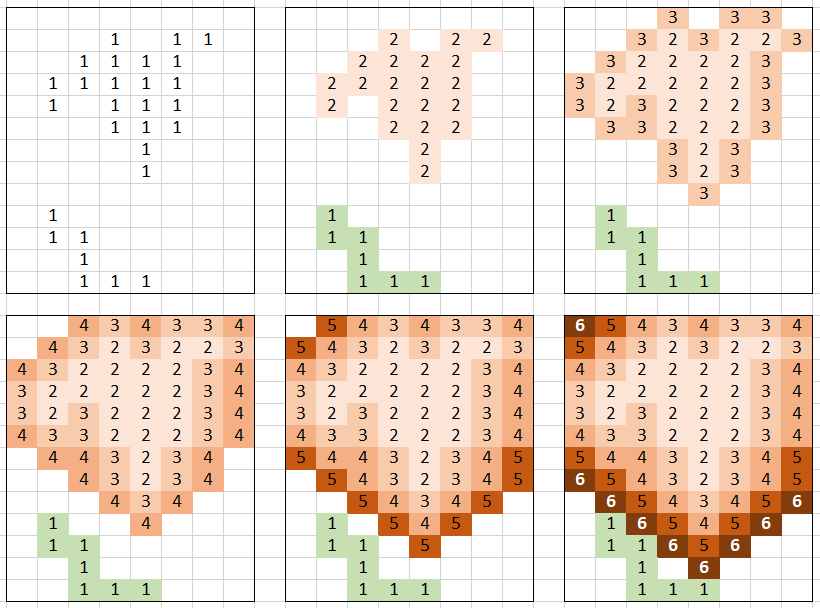
Conceptually, our method is very straightforward: find both islands, then for one of the islands, keep "growing" it by 1 until we touch the second island.

We can use a depth-first search to find the islands, and a breadth-first search to "grow" one of them. This leads to a verbose but correct solution.

Algorithm

To find both islands, look for a square with a 1 we haven't visited, and dfs to get the component of that region. Do this twice. After, we have two components source and target.

To find the shortest bridge, do a BFS from the nodes source. When we reach any node in target, we will have found the shortest distance.

Please see the code for more implementation details.

  public int shortestBridge(int[][] A) {

    int R = A.length, C = A[0].length;

    int[][] colors = getComponents(A);

    Queue<Node> queue = new LinkedList();

    Set<Integer> seen = new HashSet();

    Set<Integer> target = new HashSet();

    for (int r = 0; r < R; ++r)

      for (int c = 0; c < C; ++c) {

        if (colors[r][c] == 1) {

          seen.add(r * R + c);

          queue.add(new Node(r, c, 0));

        } else if (colors[r][c] == 2) {

          target.add(r * R + c);

        }

      }

    while (!queue.isEmpty()) {

      Node node = queue.poll();

      if (target.contains(node.r * R + node.c))

        return node.depth - 1;

      for (int nei : neighbors(A, node.r, node.c)) {

        int nr = nei / R, nc = nei % R;

        if (colors[nr][nc] != 1) {

          queue.add(new Node(nr, nc, node.depth + 1));

          colors[nr][nc] = 1;

        }

      }

    }

    throw null;

  }

  public int[][] getComponents(int[][] A) {

    int R = A.length, C = A[0].length;

    int[][] colors = new int[R][C];

    int t = 0;

    for (int r0 = 0; r0 < R; ++r0)

      for (int c0 = 0; c0 < C; ++c0)

        if (colors[r0][c0] == 0 && A[r0][c0] == 1) {

          // Start dfs

          Stack<Integer> stack = new Stack();

          stack.push(r0 * R + c0);

          colors[r0][c0] = ++t;

          while (!stack.isEmpty()) {

            int node = stack.pop();

            int r = node / R, c = node % R;

            for (int nei : neighbors(A, r, c)) {

              int nr = nei / R, nc = nei % R;

              if (A[nr][nc] == 1 && colors[nr][nc] == 0) {

                colors[nr][nc] = t;

                stack.push(nr * R + nc);

              }

            }

          }

        }

    return colors;

  }

  public List<Integer> neighbors(int[][] A, int r, int c) {

    int R = A.length, C = A[0].length;

    List<Integer> ans = new ArrayList();

    if (0 <= r - 1)

      ans.add((r - 1) * R + c);

    if (0 <= c - 1)

      ans.add(r * R + (c - 1));

    if (r + 1 < R)

      ans.add((r + 1) * R + c);

    if (c + 1 < C)

      ans.add(r * R + (c + 1));

    return ans;

  }

class Node {

  int r, c, depth;

  Node(int r, int c, int d) {

    this.r = r;

    this.c = c;

    depth = d;

  }

}

https://leetcode.com/problems/shortest-bridge/discuss/189235/Java-Bidirectional-BFS

A[x][y]=0: it is an unexplored empty cell
A[x][y]=1: it is an island to be explored
A[x][y]=2: it is an island that has been explored
A[x][y]=3: this cell is already captured by island a
A[x][y]=4: this cell is already captured by island b

First there are only 0 and 1 in board, we store island A in qa, and island B in qb. Then we do BFS from those 2 islands, step by step. When one island reaches a cell that has been captured by the other island, we return the cost stored in res.

3，4的更新非常聪明，有点儿像交叉染色 如果不加这个smart的处理的话，那么对于其中一个island中的所有点都要进行一遍BFS 然后进行比较 就会超出时间限制 学习了！

    public int shortestBridge(int[][] A) {
        Queue<int[]> qa= new LinkedList<>();
        Queue<int[]> qb= new LinkedList<>();
        int m=A.length, n=A[0].length;
        for (int i=0; i<m; i++){
            for (int j=0; j<n; j++){
                if (A[i][j]==1) {
                    if (qa.isEmpty()) dfs(A, i, j, qa);
                    else dfs(A, i, j, qb);
                }
            }
        }
        int res=0;
        int[] d= new int[]{0,1,0,-1,0};
        while (!qa.isEmpty() && !qb.isEmpty()){
            for (int size=qa.size(); size>0; size--){
                int[] cur= qa.poll();
                for (int k=0; k<4; k++){
                    int x= cur[0]+d[k], y= cur[1]+d[k+1];
                    if (x<0 || x>=m || y<0 || y>=n || A[x][y]==3 || A[x][y]==2) continue; // Thanks Evolut1on for pointing this out, we can also skip A[x][y]==2
                    if (A[x][y]==4) return res;
                    A[x][y]=3;
                    qa.add(new int[]{x, y});
                }
            }
            for (int size=qb.size(); size>0; size--){
                int[] cur= qb.poll();
                for (int k=0; k<4; k++){
                    int x= cur[0]+d[k], y= cur[1]+d[k+1];
                    if (x<0 || x>=m || y<0 || y>=n || A[x][y]==4 || A[x][y]==2) continue; 
                    if (A[x][y]==3) return res+1;
                    A[x][y]=4;
                    qb.add(new int[]{x, y});
                }
            }
            res+=2;
        }
        return 1;
    }
    public void dfs(int[][] A, int i, int j, Queue<int[]> q){
        int m=A.length, n=A[0].length;
        if (i<0 || i>=m || j<0 || j>=n || A[i][j]!=1) return;
        q.add(new int[]{i, j});
        A[i][j]=2;
        dfs(A, i+1, j, q);
        dfs(A, i-1, j, q);
        dfs(A, i, j+1, q);
        dfs(A, i, j-1, q);
    }