Related: LeetCode 785 - Is Graph Bipartite?
https://leetcode.com/problems/possible-bipartition/
X. BFS
https://leetcode.com/problems/possible-bipartition/discuss/159085/java-graph
X. Union Find
https://leetcode.com/problems/possible-bipartition/discuss/173898/Java-Union-Find-Solution
https://leetcode.com/problems/possible-bipartition/discuss/189002/Easy-to-understand-c%2B%2B-topological-sort
https://leetcode.com/problems/possible-bipartition/
Given a set of
N people (numbered 1, 2, ..., N), we would like to split everyone into two groups of any size.
Each person may dislike some other people, and they should not go into the same group.
Formally, if
dislikes[i] = [a, b], it means it is not allowed to put the people numbered a and b into the same group.
Return
X. DFS
http://www.noteanddata.com/leetcode-886-Possible-Bipartition-java-solution-note.html#时间复杂度
每个节点访问一次, 每个dislike也访问一次, 相当于O(N+E), N是节点个数, E是边的个数
空间复杂度
新建了一个allList, 相当于E2的大小, 然后一个groupTable的大小是N, 那就是O(E2+N)
https://zxi.mytechroad.com/blog/graph/leetcode-886-possible-bipartition/
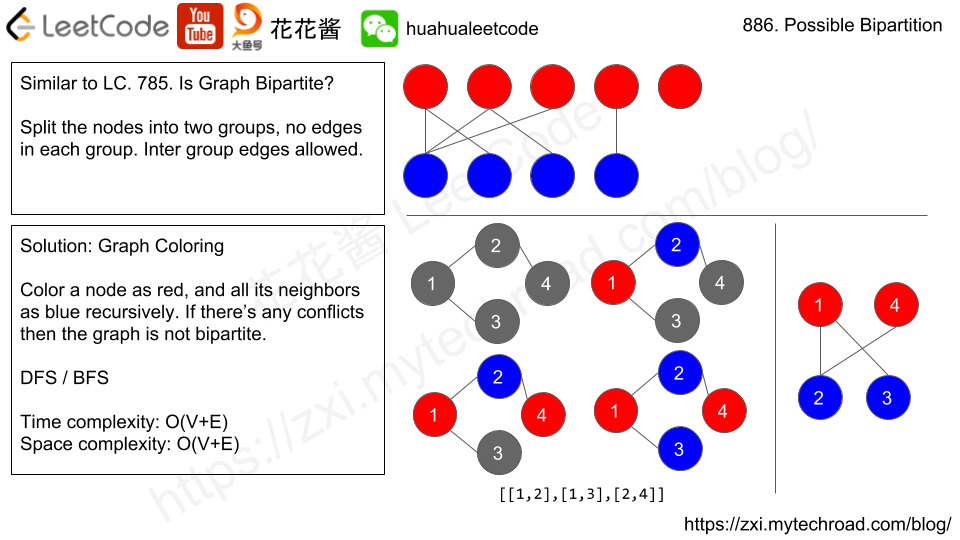
Solution: Graph Coloring
Color a node with one color, and color all it’s disliked nodes with another color, if can not finish return false.
Time complexity: O(V+E)
Space complexity: O(V+E)
true if and only if it is possible to split everyone into two groups in this way.X. DFS
http://www.noteanddata.com/leetcode-886-Possible-Bipartition-java-solution-note.html#时间复杂度
- 这个题目的意思是二分图问题(我之前并不知道这个),关于二分图有一系列问题和对应的算法,后面有时间准备系统学习一下
- 对于这个分组,首先第一个人,可以在两个组里面随意选一个,结果并不会有不同,所以不需要完全枚举所有的可能性
- 选了第一个人以后,所有这个人dislike的人,只能选第二组,否则就冲突
- 进一步,那些被放到第二组里面的人dislike的那些人,只能放会第一组。然后可以继续循环
- 所以, 这个过程就是一个dfs的过程, 选了第一个人以后,可以把后面所有能够关联到的人都分好组。
然后对于每一个节点,如果已经在前面的dfs被分组, 那么就不能在随意分了,
如果并没有被分组, 那么意味着这个节点,以及所有这个节点能够关联到的所有节点,以及按index访问后面没有被分组的节点,都和前面已经被分组的所有节点没有关联,
否则的话一定已经被分组了。 这时候,又相当于回到步骤2, 可以在两个组里面随意选一个组,结果不会有不同 - 如果在上面dfs的过程中,遇到了冲突, 那么就不能分组。 如果所有节点都放完了没有冲突,那就可以分组
- 所谓冲突, 就是一个人已经被放到一个组里面,然后在dfs的过程中,发现应该要放到另外一个组里面
比如[[1,2],[1,3],[2,3]], 首先把1放到组1, 把2放到组2, 然后把3放到组1, 这时候到[1,3], 发现要把3放到组2, 但是3已经在组2了,
所以就冲突了
每个节点访问一次, 每个dislike也访问一次, 相当于O(N+E), N是节点个数, E是边的个数
空间复杂度
新建了一个allList, 相当于E2的大小, 然后一个groupTable的大小是N, 那就是O(E2+N)
https://zxi.mytechroad.com/blog/graph/leetcode-886-possible-bipartition/
Solution: Graph Coloring
Color a node with one color, and color all it’s disliked nodes with another color, if can not finish return false.
Time complexity: O(V+E)
Space complexity: O(V+E)
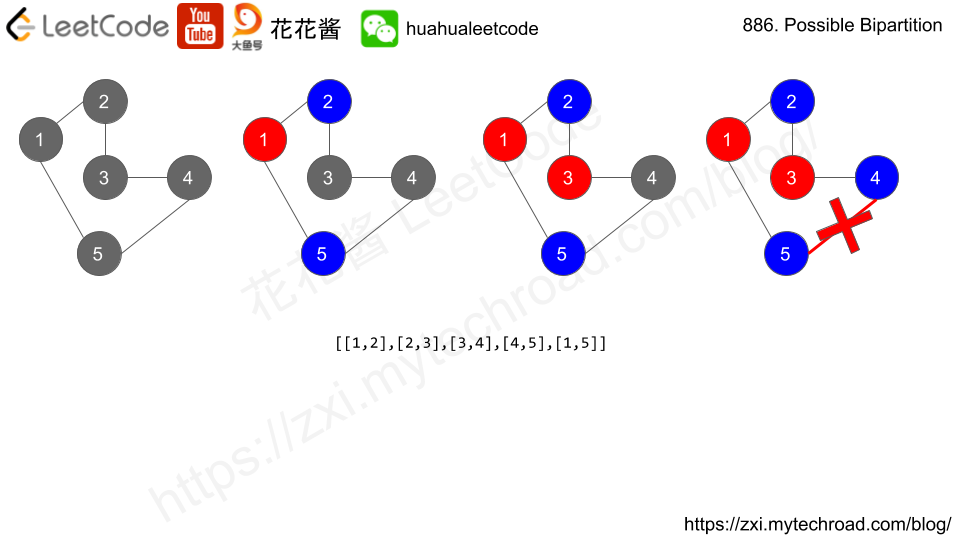
It's natural to try to assign everyone to a group. Let's say people in the first group are red, and people in the second group are blue.
If the first person is red, anyone disliked by this person must be blue. Then, anyone disliked by a blue person is red, then anyone disliked by a red person is blue, and so on.
If at any point there is a conflict, the task is impossible, as every step logically follows from the first step. If there isn't a conflict, then the coloring was valid, so the answer would be
true.
Algorithm
Consider the graph on
N people formed by the given "dislike" edges. We want to check that each connected component of this graph is bipartite.
For each connected component, we can check whether it is bipartite by just trying to coloring it with two colors. How to do this is as follows: color any node red, then all of it's neighbors blue, then all of those neighbors red, and so on. If we ever color a red node blue (or a blue node red), then we've reached a conflict.
- Time Complexity: , where is the length of
dislikes. - Space Complexity: .
ArrayList<Integer>[] graph;
Map<Integer, Integer> color;
public boolean possibleBipartition(int N, int[][] dislikes) {
graph = new ArrayList[N + 1];
for (int i = 1; i <= N; ++i)
graph[i] = new ArrayList();
for (int[] edge : dislikes) {
graph[edge[0]].add(edge[1]);
graph[edge[1]].add(edge[0]);
}
color = new HashMap();
for (int node = 1; node <= N; ++node)
if (!color.containsKey(node) && !dfs(node, 0))
return false;
return true;
}
public boolean dfs(int node, int c) {
if (color.containsKey(node))
return color.get(node) == c;
color.put(node, c);
for (int nei : graph[node])
if (!dfs(nei, c ^ 1))
return false;
return true;
}
https://leetcode.com/problems/possible-bipartition/discuss/158957/Java-DFS-solutionhttps://leetcode.com/problems/possible-bipartition/discuss/159085/java-graph
public boolean possibleBipartition(int N, int[][] dislikes) {
int[] color = new int[N + 1];
List<List<Integer>> adj = new ArrayList<>(N + 1);
for(int i = 0; i <= N; i++) adj.add(new ArrayList<Integer>());
for(int[] d : dislikes) {
adj.get(d[0]).add(d[1]);
adj.get(d[1]).add(d[0]);
}
for(int i = 1; i <= N; i++) {
if(color[i] == 0) {
color[i] = 1;
Queue<Integer> q = new LinkedList<>();
q.add(i);
while(!q.isEmpty()) {
int cur = q.poll();
for(int nb : adj.get(cur)) {
if(color[nb] == 0) {
color[nb] = color[cur] == 1 ? 2 : 1;
q.add(nb);
} else {
if(color[nb] == color[cur]) return false;
}
}
}
}
}
return true;
}
https://leetcode.com/problems/possible-bipartition/discuss/173898/Java-Union-Find-Solution
public boolean possibleBipartition(int N, int[][] dislikes) {
int[] colors = new int[N + 1];
for(int i = 1; i <= N; ++i) colors[i] = i;
for(int i = 0; i < dislikes.length; ++i) {
int p1 = dislikes[i][0], p2 = dislikes[i][1];
if(colors[p2] == p2) colors[p2] = p1;
else {
int[] uf1 = find(p1, colors), uf2 = find(p2, colors);
if(uf1[0] == uf2[0] && uf1[1] == uf2[1]) return false;
}
}
return true;
}
private int[] find(int p, int[] colors) {
int color = 0;
while(colors[p] != p) {
p = colors[p];
color = color == 0 ? 1 : 0;
}
return new int[] {p, color};
}
public boolean possibleBipartition(int N, int[][] dislikes) {
int[] parent = new int[N + 1];
for (int i = 0; i <= N; i++) parent[i] = i;
Map<Integer, List<Integer>> map = new HashMap<>();
for (int[] pair : dislikes) {
int a = pair[0];
int b = pair[1];
map.putIfAbsent(a, new ArrayList<>());
map.putIfAbsent(b, new ArrayList<>());
map.get(a).add(b);
map.get(b).add(a);
}
for (int i = 1; i <= N; i++) {
if (map.containsKey(i)) {
int parent1 = find(parent, i);
List<Integer> opponents = map.get(i);
int parent2 = find(parent, opponents.get(0));
if (parent1 == parent2) return false;
for (int j = 1; j < opponents.size(); j++) {
int opponentParent = find(parent, opponents.get(j));
if (parent1 == opponentParent) return false;
parent[opponentParent] = parent2;
}
}
}
return true;
}
private int find(int[] parent, int i) {
while (i != parent[i]) {
i = parent[parent[i]];
}
return i;
}
https://leetcode.com/problems/possible-bipartition/discuss/189002/Easy-to-understand-c%2B%2B-topological-sort