LeetCode 885 - Spiral Matrix III

https://leetcode.com/problems/spiral-matrix-iii/

On a 2 dimensional grid with R rows and C columns, we start at (r0, c0) facing east.

Here, the north-west corner of the grid is at the first row and column, and the south-east corner of the grid is at the last row and column.

Now, we walk in a clockwise spiral shape to visit every position in this grid. 

Whenever we would move outside the boundary of the grid, we continue our walk outside the grid (but may return to the grid boundary later.) 

Eventually, we reach all R * C spaces of the grid.

Return a list of coordinates representing the positions of the grid in the order they were visited.

Example 1:

Input: R = 1, C = 4, r0 = 0, c0 = 0
Output: [[0,0],[0,1],[0,2],[0,3]]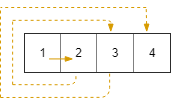

Example 2:

Input: R = 5, C = 6, r0 = 1, c0 = 4
Output: [[1,4],[1,5],[2,5],[2,4],[2,3],[1,3],[0,3],[0,4],[0,5],[3,5],[3,4],[3,3],[3,2],[2,2],[1,2],[0,2],[4,5],[4,4],[4,3],[4,2],[4,1],[3,1],[2,1],[1,1],[0,1],[4,0],[3,0],[2,0],[1,0],[0,0]]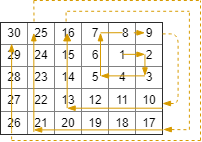

https://leetcode.com/problems/spiral-matrix-iii/discuss/158977/Java-15-lines-concise-solution-with-comments

    public int[][] spiralMatrixIII(int R, int C, int r0, int c0) {
        int[][] dirt = new int[][]{{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; // east, south, west, north
        List<int[]> res = new ArrayList<>();
        int len = 0, d = 0; // move <len> steps in the <d> direction
        res.add(new int[]{r0, c0});
        while (res.size() < R * C) {
            if (d == 0 || d == 2) len++; // when move east or west, the length of path need plus 1 
            for (int i = 0; i < len; i++) {
                r0 += dirt[d][0];
                c0 += dirt[d][1];
                if (r0 >= 0 && r0 < R && c0 >= 0 && c0 < C) // check valid
                    res.add(new int[]{r0, c0});
            }
            d = (d + 1) % 4; // turn to next direction
        }
        return res.toArray(new int[R * C][2]);
    }

We can walk in a spiral shape from the starting square, ignoring whether we stay in the grid or not. Eventually, we must have reached every square in the grid.

Algorithm

Examining the lengths of our walk in each direction, we find the following pattern: 1, 1, 2, 2, 3, 3, 4, 4, ... That is, we walk 1 unit east, then 1 unit south, then 2 units west, then 2 units north, then 3 units east, etc. Because our walk is self-similar, this pattern repeats in the way we expect.

After, the algorithm is straightforward: perform the walk and record positions of the grid in the order we visit them. Please read the inline comments for more details.

• Time Complexity: $O((\max(R, C))^2)$. Potentially, our walk needs to spiral until we move $R$ in one direction, and $C$ in another direction, so as to reach every cell of the grid.
• Space Complexity: $O(R * C)$, the space used by the answer. 

  public int[][] spiralMatrixIII(int R, int C, int r0, int c0) {

    int[] dr = new int[] { 0, 1, 0, -1 };

    int[] dc = new int[] { 1, 0, -1, 0 };

    int[][] ans = new int[R * C][2];

    int t = 0;

    ans[t++] = new int[] { r0, c0 };

    if (R * C == 1)

      return ans;

    for (int k = 1; k < 2 * (R + C); k += 2)

      for (int i = 0; i < 4; ++i) { // i: direction index

        int dk = k + (i / 2); // number of steps in this direction

        for (int j = 0; j < dk; ++j) { // for each step in this direction...

          // step in the i-th direction

          r0 += dr[i];

          c0 += dc[i];

          if (0 <= r0 && r0 < R && 0 <= c0 && c0 < C) {

            ans[t++] = new int[] { r0, c0 };

            if (t == R * C)

              return ans;

          }

        }

      }

    throw null;

  }

https://leetcode.com/problems/spiral-matrix-iii/discuss/158970/C%2B%2BJavaPython-112233-Steps

Intuition:
Take steps one by one.
If the location is inside of grid, add it to res.
But how to simulate the path?

It seems to be annoying, but if we oberserve the path:

move right 1 step, turn right
move down 1 step, turn right
move left 2 steps, turn right
move top 2 steps, turn right,
move right 3 steps, turn right
move down 3 steps, turn right
move left 4 steps, turn right
move top 4 steps, turn right,

we can find the sequence of steps: 1,1,2,2,3,3,4,4,5,5....

So there are two thing to figure out:

1. how to generate sequence 1,1,2,2,3,3,4,4,5,5
2. how to turn right?

Generate sequence 1,1,2,2,3,3,4,4,5,5
Let n be index of this sequence.
Then A0 = 1, A1 = 1, A2 = 2 ......
We can include that An = n / 2 + 1

How to turn right?
By cross product:
Assume current direction is (x, y) in plane, which is (x, y, 0) in space.
Then the direction after turn right (x, y, 0) × (0, 0, 1) = (y, -x, 0)
Translate to code: tmp = x; x = y; y = -tmp;

By arrays of arrays:
The directions order is (0,1),(1,0),(0,-1),(-1,0), then repeat.
Just define a variable.

    public int[][] spiralMatrixIII(int R, int C, int r, int c) {
        int[][] res = new int[R * C][2];
        res[0] = new int[] {r, c};
        int x = 0, y = 1, n = 0, i = 0, tmp, j = 1;
        while (j < R * C) {
            r += x; c += y; i++;
            if (0 <= r && r < R && 0 <= c && c < C)
                res[j++] = new int[] {r, c};
            if (i == n / 2 + 1) {
                i = 0; n++; tmp = x; x = y; y = -tmp;
            }
        }
        return res;
    }

https://leetcode.com/problems/spiral-matrix-iii/discuss/158954/JAVA-Simulation-17-lines-with-line-by-line-Explanation

    public int[][] spiralMatrixIII(int R, int C, int r0, int c0) {
        int[][] res= new int[R*C][2];
        res[0]=new int[]{r0, c0};
        int len=0, idx=1, k=0;
        int[] d= new int[]{0,1,0,-1,0};
        while (idx<R*C){
            len++;
            for (int round=0; round<2; round++){
                for (int sz=len; sz>0; sz--){
                    r0+=d[k];
                    c0+=d[k+1];
                    if (r0<0 || r0>=R || c0<0 || c0>=C) continue;
                    res[idx++]=new int[]{r0, c0};
                }
                k=(k+1)%4;
            }
        }
        return res;
    }

X. https://leetcode.com/problems/spiral-matrix-iii/discuss/158971/Python-Sort-All-Coordinates

Put all valid coordinates to a list res

Sort all coordinates by the following rule:

0. Change coordinates to a relative coordinates to center.
1. Sort ascending by the distance to the center max(abs(x), abs(y))
   If max(abs(x), abs(y)) == 0, it's the center.
   If max(abs(x), abs(y)) == 1, it's in the first layer around the center
2. Sort descending by the angle to the center max(abs(x), abs(y))

    def spiralMatrixIII(self, R, C, r, c):
        def key((x, y)):
            x, y = x - r, y - c
            return (max(abs(x), abs(y)), -((math.atan2(-1, 1) - math.atan2(x, y)) % (math.pi * 2)))
        return sorted([(i, j) for i in xrange(R) for j in xrange(C)], key=key)

X. https://blog.csdn.net/XX_123_1_RJ/article/details/81952905
这题目，可以这样简单解决，不管什么二维数组是多大的，我就每次走一个螺旋，但是在添加路径的时候，判断当前位置是否出界，如果出界，就不往路径里面添加，这样的好处是代码非常简单的实现，缺是点要走很多不必要的路径，可以使用剪枝的方法来处理。在走螺旋的时候，其实是找规律1、1、2、2、3、3（左、下、右、上、左、下、右、上….）

代码参考官方：leetcode.com/problems/spiral-matrix-iii/solution/ （给人的感觉是很清晰，但是效率不高，可以剪枝改进）

    def spiralMatrixIII(self, R, C, r0, c0):
        res = [[r0, c0]]
        if R * C == 1: return res
        for k in range(1, 2*(R+C), 2):  # k 表示每个边的长度
            for dr, dc, dk in ((0, 1, k), (1, 0, k), (0, -1, k+1), (-1, 0, k+1)):  # 左、下、右、上 (四个方向移动)
                for _ in range(dk):
                    r0 += dr
                    c0 += dc
                    if 0 <= r0 < R and 0 <= c0 < C:  # 判断是否出界
                        res.append([r0, c0])  # 添加路径
                        if len(res) == R * C:  # 够长了，说明已经走完
                            return res


if __name__ == '__main__':
    R, C, r0, c0 = 5,  6, 1, 4
    solu = Solution()
    print(solu.spiralMatrixIII(R, C, r0, c0))


https://leetcode.com/problems/spiral-matrix-iii/discuss/163370/Simple-East-to-Understand-Java-solution
The idea here is that once we start at (r=r0, c=c0), we walk along the east, then south, then west, and then north.

When we go east, we do c++ (column increases), when we go west, we do c--, when we go south, we do r++ (row increases), and when we go north, we do r--.

After starting at (r0,c0), we need to walk in spirals, where the length of the spiral increases after every two directions. For example 2, we start at (r0=1, c0=4), then we go east by one length, we go south by one length. Following that, we go west by 2 length and then, go north by 2 length. After that, we go in next directions by 3 lengths, and so on.

The trick here is that we continue to walk in spiral, whether the current (r,c) is valid or not. However, we add (r,c) to the result only if it is valid.

    int idx;
    int[][] ret;
    
    private void add (int r, int c, int R, int C) {
        if (r >= R || r < 0 || c >= C || c < 0) return;
        ret[idx][0] = r;
        ret[idx++][1] = c;
    }
    
    public int[][] spiralMatrixIII(int R, int C, int r0, int c0) {
        int r = r0, c = c0, len = 1;
        ret = new int[R * C][2];
        while (idx < (R * C )) {         
            for (int k = 0; k < len; k++) add(r, c++, R, C);          
            for (int k = 0; k < len; k++) add(r++, c, R, C);
            len++;
            for (int k = 0; k < len; k++) add(r, c--, R, C);
            for (int k = 0; k < len; k++) add(r--, c, R, C);
            len++;   
        }
        return ret;
    }