LeetCode 918 - Maximum Sum Circular Subarray

https://leetcode.com/problems/maximum-sum-circular-subarray/description/

Given a circular array C of integers represented by A, find the maximum possible sum of a non-empty subarray of C.

Here, a circular array means the end of the array connects to the beginning of the array.  (Formally, C[i] = A[i] when 0 <= i < A.length, and C[i+A.length] = C[i] when i >= 0.)

Also, a subarray may only include each element of the fixed buffer A at most once.  (Formally, for a subarray C[i], C[i+1], ..., C[j], there does not exist i <= k1, k2 <= j with k1 % A.length = k2 % A.length.)

https://leetcode.com/problems/maximum-sum-circular-subarray/discuss/178422/C%2B%2BJavaPython-One-Pass

1. The first is that the subarray take only a middle part, and we know how to find the max subarray sum.
2. The second is that the subarray take a part of head array and a part of tail array.
   We can transfer this case to the first one.
   The maximum result equals to the total sum minus the minimum subarray sum.

Here is a diagram by @motorix:

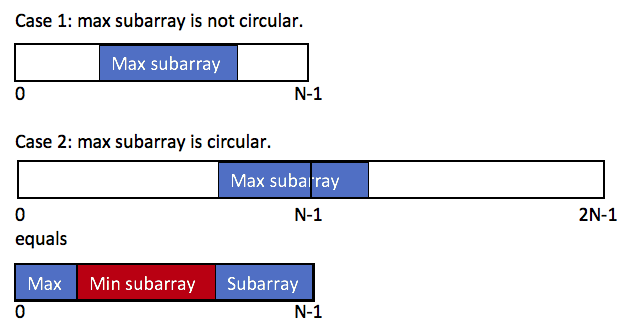
So the max subarray circular sum equals to
max(the max subarray sum, the total sum - the min subarray sum)

One** corner case** to pay attention:
If all number are negative,
return the maximum one,
(which equals to the max subarray sum)

    public int maxSubarraySumCircular(int[] A) {
        int total = 0, maxSum = -30000, curMax = 0, minSum = 30000, curMin = 0;
        for (int a : A) {
            curMax = Math.max(curMax + a, a);
            maxSum = Math.max(maxSum, curMax);
            curMin = Math.min(curMin + a, a);
            minSum = Math.min(minSum, curMin);
            total += a;
        }
        return maxSum > 0 ? Math.max(maxSum, total - minSum) : maxSum;
    }

https://leetcode.com/problems/maximum-sum-circular-subarray/discuss/178497/Short-Java-Solution!!!

    public int maxSubarraySumCircular(int[] A) {
        int localMax = -30001, globalMax = -30001, localMin = 30001, globalMin  = 30001, sum = 0;
        for(int e : A) {
            sum += e;
            localMax = Math.max(localMax + e, e);
            localMin = Math.min(localMin + e, e);
            globalMax = Math.max(globalMax, localMax);
            globalMin = Math.min(globalMin, localMin);
        }
        return globalMax > 0 ? Math.max(globalMax, sum - globalMin) : globalMax;
    }

Approach 3: Kadane's (Sign Variant)

As in Approach 1, subarrays of circular arrays can be classified as either as one-interval subarrays, or two-interval subarrays.

Using Kadane's algorithm kadane for finding the maximum sum of non-empty subarrays, the answer for one-interval subarrays is kadane(A).

Now, let $N = A\text{.length}$. For a two-interval subarray like:

$(A_0 + A_1 + \cdots + A_i) + (A_j + A_{j+1} + \cdots + A_{N - 1})$

we can write this as

$(\sum_{k=0}^{N-1} A_k) - (A_{i+1} + A_{i+2} + \cdots + A_{j-1})$

For two-interval subarrays, let $B$ be the array $A$ with each element multiplied by $-1$. Then the answer for two-interval subarrays is $\text{sum}(A) + \text{kadane}(B)$.

Except, this isn't quite true, as if the subarray of $B$ we choose is the entire array, the resulting two interval subarray $[0, i] + [j, N-1]$ would be empty.

We can remedy this problem by doing Kadane twice: once on $B$ with the first element removed, and once on $B$with the last element removed.

  public int maxSubarraySumCircular(int[] A) {

    int S = 0; // S = sum(A)

    for (int x : A)

      S += x;

    int ans1 = kadane(A, 0, A.length - 1, 1);

    int ans2 = S + kadane(A, 1, A.length - 1, -1);

    int ans3 = S + kadane(A, 0, A.length - 2, -1);

    return Math.max(ans1, Math.max(ans2, ans3));

  }

  public int kadane(int[] A, int i, int j, int sign) {

    // The maximum non-empty subarray for array

    // [sign * A[i], sign * A[i+1], ..., sign * A[j]]

    int ans = Integer.MIN_VALUE;

    int cur = Integer.MIN_VALUE;

    for (int k = i; k <= j; ++k) {

      cur = sign * A[k] + Math.max(cur, 0);

      ans = Math.max(ans, cur);

    }

    return ans;

  }

As in Approach 3, subarrays of circular arrays can be classified as either as one-interval subarrays (which we can use Kadane's algorithm), or two-interval subarrays.

We can modify Kadane's algorithm to use min instead of max. All the math in our explanation of Kadane's algorithm remains the same, but the algorithm lets us find the minimum sum of a subarray instead.

For a two interval subarray written as $(\sum_{k=0}^{N-1} A_k) - (\sum_{k=i+1}^{j-1} A_k)$, we can use our kadane-min algorithm to minimize the "interior" $(\sum_{k=i+1}^{j-1} A_k)$ part of the sum.

Again, because the interior $[i+1, j-1]$ must be non-empty, we can break up our search into a search on A[1:] and on A[:-1].

  public int maxSubarraySumCircular(int[] A) {

    // S: sum of A

    int S = 0;

    for (int x : A)

      S += x;

    // ans1: answer for one-interval subarray

    int ans1 = Integer.MIN_VALUE;

    int cur = Integer.MIN_VALUE;

    for (int x : A) {

      cur = x + Math.max(cur, 0);

      ans1 = Math.max(ans1, cur);

    }

    // ans2: answer for two-interval subarray, interior in A[1:]

    int ans2 = Integer.MAX_VALUE;

    cur = Integer.MAX_VALUE;

    for (int i = 1; i < A.length; ++i) {

      cur = A[i] + Math.min(cur, 0);

      ans2 = Math.min(ans2, cur);

    }

    ans2 = S - ans2;

    // ans3: answer for two-interval subarray, interior in A[:-1]

    int ans3 = Integer.MAX_VALUE;

    cur = Integer.MAX_VALUE;

    for (int i = 0; i < A.length - 1; ++i) {

      cur = A[i] + Math.min(cur, 0);

      ans3 = Math.min(ans3, cur);

    }

    return Math.max(ans1, Math.max(ans2, ans3));

  }

#Kadane's algorithm
ans = cur = None
for x in A:
    cur = x + max(cur, 0)
    ans = max(ans, cur)
return ans

Subarrays of circular arrays can be classified as either as one-interval subarrays, or two-interval subarrays, depending on how many intervals of the fixed-size buffer A are required to represent them.

For example, if A = [0, 1, 2, 3, 4, 5, 6] is the underlying buffer of our circular array, we could represent the subarray [2, 3, 4] as one interval $[2, 4]$, but we would represent the subarray [5, 6, 0, 1] as two intervals $[5, 6], [0, 1]$.

Using Kadane's algorithm, we know how to get the maximum of one-interval subarrays, so it only remains to consider two-interval subarrays.

Let's say the intervals are $[0, i], [j, A\text{.length} - 1]$. Let's try to compute the i-th candidate: the largest possible sum of a two-interval subarray for a given $i$. Computing the $[0, i]$ part of the sum is easy. Let's write

$T_j = A[j] + A[j+1] + \cdots + A[A\text{.length} - 1]$

and

$R_j = \max\limits_{k \geq j} T_k$

so that the desired i-th candidate is:

$(A[0] + A[1] + \cdots + A[i]) + R_{i+2}$

Since we can compute $T_j$ and $R_j$ in linear time, the answer is straightforward after this setup.

  public int maxSubarraySumCircular(int[] A) {

    int N = A.length;

    int ans = A[0], cur = A[0];

    for (int i = 1; i < N; ++i) {

      cur = A[i] + Math.max(cur, 0);

      ans = Math.max(ans, cur);

    }

    // ans is the answer for 1-interval subarrays.

    // Now, let's consider all 2-interval subarrays.

    // For each i, we want to know

    // the maximum of sum(A[j:]) with j >= i+2

    // rightsums[i] = A[i] + A[i+1] + ... + A[N-1]

    int[] rightsums = new int[N];

    rightsums[N - 1] = A[N - 1];

    for (int i = N - 2; i >= 0; --i)

      rightsums[i] = rightsums[i + 1] + A[i];

    // maxright[i] = max_{j >= i} rightsums[j]

    int[] maxright = new int[N];

    maxright[N - 1] = A[N - 1];

    for (int i = N - 2; i >= 0; --i)

      maxright[i] = Math.max(maxright[i + 1], rightsums[i]);

    int leftsum = 0;

    for (int i = 0; i < N - 2; ++i) {

      leftsum += A[i];

      ans = Math.max(ans, leftsum + maxright[i + 2]);

    }

    return ans;

  }

X. Approach 2: Prefix Sums + Monoqueue

First, we can frame the problem as a problem on a fixed array.

We can consider any subarray of the circular array with buffer A, to be a subarray of the fixed array A+A.

For example, if A = [0,1,2,3,4,5] represents a circular array, then the subarray [4,5,0,1] is also a subarray of fixed array [0,1,2,3,4,5,0,1,2,3,4,5]. Let B = A+A be this fixed array.

Now say $N = A\text{.length}$, and consider the prefix sums

$P_k = B[0] + B[1] + \cdots + B[k-1]$

Then, we want the largest $P_j - P_i$ where $j - i \leq N$.

Now, consider the j-th candidate answer: the best possible $P_j - P_i$ for a fixed $j$. We want the $i$ so that $P_i$ is smallest, with $j - N \leq i &lt; j$. Let's call this the optimal i for the j-th candidate answer. We can use a monoqueue to manage this.

Algorithm

Iterate forwards through $j$, computing the $j$-th candidate answer at each step. We'll maintain a queue of potentially optimal $i$'s.

The main idea is that if $i_1 &lt; i_2$ and $P_{i_1} \geq P_{i_2}$, then we don't need to remember $i_1$ anymore.

Please see the inline comments for more algorithmic details about managing the queue.

  public int maxSubarraySumCircular(int[] A) {

    int N = A.length;

    // Compute P[j] = B[0] + B[1] + ... + B[j-1]

    // for fixed array B = A+A

    int[] P = new int[2 * N + 1];

    for (int i = 0; i < 2 * N; ++i)

      P[i + 1] = P[i] + A[i % N];

    // Want largest P[j] - P[i] with 1 <= j-i <= N

    // For each j, want smallest P[i] with i >= j-N

    int ans = A[0];

    // deque: i's, increasing by P[i]

    Deque<Integer> deque = new ArrayDeque();

    deque.offer(0);

    for (int j = 1; j <= 2 * N; ++j) {

      // If the smallest i is too small, remove it.

      if (deque.peekFirst() < j - N)

        deque.pollFirst();

      // The optimal i is deque[0], for cand. answer P[j] - P[i].

      ans = Math.max(ans, P[j] - P[deque.peekFirst()]);

      // Remove any i1's with P[i2] <= P[i1].

      while (!deque.isEmpty() && P[j] <= P[deque.peekLast()])

        deque.pollLast();

      deque.offerLast(j);

    }

    return ans;

  }