https://leetcode.com/problems/flip-string-to-monotone-increasing/
X.
https://www.cnblogs.com/seyjs/p/9828593.html
转换后的字符串有两种形式,一个是全为0,另一个是前半部分全是0后半部分全是1。第一种情况的翻转次数是S中1的个数;第二种的情况,我们只要找出转换后的字符串第一个1所在的位置即可。设第一个所在的位置是i,那么S[0:i-1]区间内所有1都要变成0,而S[i:-1]区间内所有的0要变成1,总的翻转次数就是前一段区间内1的个数加上后一段区间内0的个数即可。遍历S,即可求出第二种情况的最小值,再与第一种情况求得的值比较取最小值即可。
https://leetcode.com/problems/flip-string-to-monotone-increasing/discuss/189751/C%2B%2B-one-pass-DP-solution-0ms-O(n)-or-O(1)-one-line-with-explaination.
https://leetcode.com/problems/flip-string-to-monotone-increasing/discuss/183862/Count-prefix-ones-and-suffix-zeros
Then
X. https://leetcode.com/problems/flip-string-to-monotone-increasing/discuss/183855/Java-DP-solution-O(n)-time-O(1)-space
X. https://zhanghuimeng.github.io/post/leetcode-926-flip-string-to-monotone-increasing/
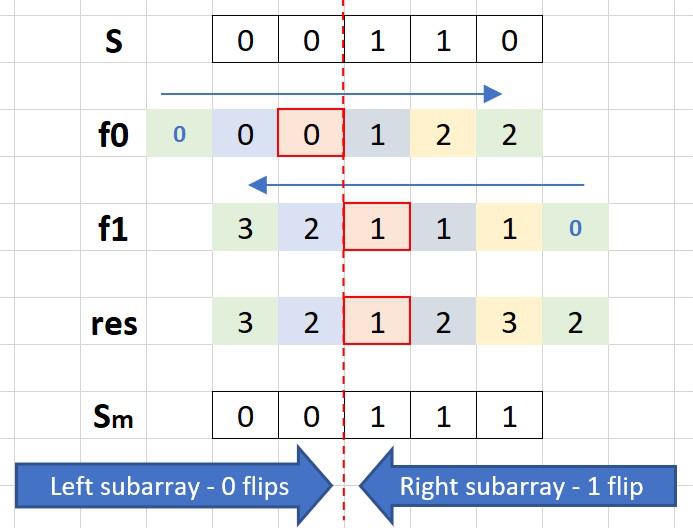
We need to split the array into left '0' and right '1' sub-arrays, so that sum of '1' -> '0' flips (left) and '0' -> '1' flips (right) is minimal.
This reminds me of 122. Best Time to Buy and Sell Stock III. That problem has a DP solution with O(1) memory complexity, so we can try to apply it here. We can go left to right, and virtually 'move' the split point every time we see that we need less '0' -> '1' than '1' -> '0' flips (
A string of
'0's and '1's is monotone increasing if it consists of some number of '0's (possibly 0), followed by some number of '1's (also possibly 0.)
We are given a string
S of '0's and '1's, and we may flip any '0' to a '1' or a '1' to a '0'.
Return the minimum number of flips to make
S monotone increasing.
https://zxi.mytechroad.com/blog/dynamic-programming/leetcode-926-flip-string-to-monotone-increasing/
https://blog.csdn.net/fuxuemingzhu/article/details/83247054
常规的做法是,我们使用Prefix数组保存每个位置之前的1有多少个。因为我们最终的目标是变成前面是0后面是1的字符串,所以,可以通过过一遍数组,要把遍历到的位置前面都变0后面都变1,需要计算每个位置前面有多少个1加上后面有多少个0。因为前面的1要翻转成0,后面的0要翻转成1.
总之,只需要先求出每个位置前面的1的个数是多少,那么,再次遍历,求每个位置前面的1个数和后面0个数的和的最小值即可。
使用的是P数组保存每个位置前面1的个数。那么后面0的个数是:总的0的个数(即,总个数减去总的1的个数) - 前面0的个数(即,现在的位置索引减去前面1的个数)。
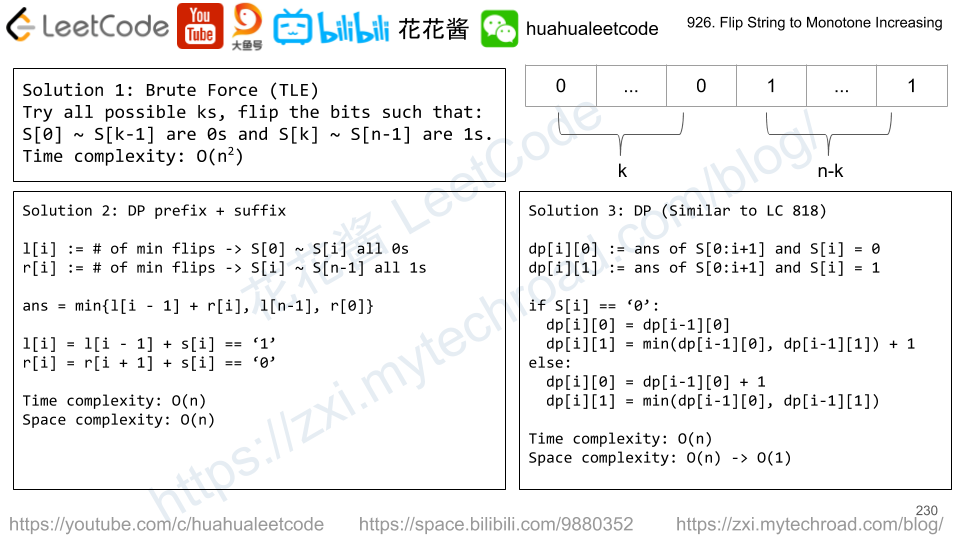
Approach 1: Prefix Sums
l[i] := number of flips to make S[0] ~ S[i] become all 0s.
r[i] := number of flips to make S[i] ~ S[n – 1] become all 1s.
Try all possible break point, S[0] ~ S[i – 1] are all 0s and S[i] ~ S[n-1] are all 1s.
ans = min{l[i – 1] + r[i]}
int minFlipsMonoIncr(string S) {
const int n = S.size();
vector<int> l(n + 1); // 1 -> 0
vector<int> r(n + 1); // 0 -> 1
l[0] = S[0] - '0';
r[n - 1] = '1' - S[n - 1];
for (int i = 1; i < n; ++i)
l[i] = l[i - 1] + S[i] - '0';
for (int i = n - 2; i >= 0; --i)
r[i] = r[i + 1] + '1' - S[i];
int ans = r[0]; // all 1s.
for (int i = 1; i <= n; ++i)
ans = min(ans, l[i - 1] + r[i]);
return ans;
}
X.
这个题和买卖股票有点类似,都需要使用一个二维dp数组,分别保存的是以0结尾或者以1结尾的字符串需要翻转的最小次数。
为了方便,给dp数组多了一个空间,表示最前面的字符串还没有开始的时候,肯定不需要做任何翻转。
那么,当我们遍历到字符串的i位置时:
如果这个位置的字符是'0',那么:
当前以0结尾的dp数组等于前面的以0结尾的dp,即不需要做任何操作,此时前面必须是0结尾;
当前以1结尾的dp数组等于Min(前面的以0结尾的dp + 1,前面的以1结尾的dp + 1)。这里的含义是一种情况为前面的0到前面的那个位置结束,把当前的0翻转成1;另一种情况是前面一位以1结束不变,把当前的0翻转成1。需要求这两个情况的最小值。此时前面可以以0或者1结尾。
如果这个位置的字符是'1',那么:
当前以0结尾的dp数组等于前面的以0结尾的dp + 1,即把当前的1翻转成0,此时前面只能以0结尾;
当前以1结尾的dp数组等于Min(前面的以0结尾的dp,前面的以1结尾的dp)。这里的含义是该位置以1结尾需要翻转多少次呢?当然是前面翻转0或者1的次数最小值,因为当前的1一定不用翻转,而前面无论怎么翻转都能满足条件。此时前面可以以0或者1结尾。
总结一下思路,首先一定要明白dp数组是代表以这个第二维度数字结尾的状态数,比如dp[i][0]就是第i个数字以0结尾的情况下,需要翻转的个数。然后,要明白的是如果遍历到的这个字符并没有限制死我们是否要翻转它,所以翻转不翻转都要考虑到,即这个对应位置变成1或者0两种情况下dp怎么更新。更新的方式是看前面一个状态,从前一个状态转成现在要变成的状态,需要做哪些操作,翻转次数怎么变化。
int minFlipsMonoIncr(string S) {
const int n = S.length();
vector<vector<int>> dp(n + 1, vector<int>(2));
for (int i = 1; i <= n; ++i) {
if (S[i - 1] == '0') {
dp[i][0] = dp[i - 1][0];
dp[i][1] = min(dp[i - 1][0], dp[i - 1][1]) + 1;
} else {
dp[i][0] = dp[i - 1][0] + 1;
dp[i][1] = min(dp[i - 1][0], dp[i - 1][1]);
}
}
return min(dp[n][0], dp[n][1]);
}
int minFlipsMonoIncr(string S) {
const int n = S.length();
int dp0 = 0;
int dp1 = 0;
for (int i = 1; i <= n; ++i) {
int tmp0 = dp0 + (S[i - 1] == '1');
dp1 = min(dp0, dp1) + (S[i - 1] == '0');
dp0 = tmp0;
}
return min(dp0, dp1);
}
https://blog.csdn.net/fuxuemingzhu/article/details/83247054
常规的做法是,我们使用Prefix数组保存每个位置之前的1有多少个。因为我们最终的目标是变成前面是0后面是1的字符串,所以,可以通过过一遍数组,要把遍历到的位置前面都变0后面都变1,需要计算每个位置前面有多少个1加上后面有多少个0。因为前面的1要翻转成0,后面的0要翻转成1.
总之,只需要先求出每个位置前面的1的个数是多少,那么,再次遍历,求每个位置前面的1个数和后面0个数的和的最小值即可。
使用的是P数组保存每个位置前面1的个数。那么后面0的个数是:总的0的个数(即,总个数减去总的1的个数) - 前面0的个数(即,现在的位置索引减去前面1的个数)。
Approach 1: Prefix Sums
For say a 5 digit string, the answer is either
'00000', '00001', '00011', '00111', '01111', or '11111'. Let's try to calculate the cost of switching to that answer. The answer has two halves, a left (zero) half, and a right (one) half.
Evidently, it comes down to a question of knowing, for each candidate half: how many ones are in the left half, and how many zeros are in the right half.
We can use prefix sums. Say
P[i+1] = A[0] + A[1] + ... + A[i], where A[i] = 1 if S[i] == '1', else A[i] = 0. We can calculate P in linear time.
Then if we want
x zeros followed by N-x ones, there are P[x] ones in the start that must be flipped, plus (N-x) - (P[N] - P[x]) zeros that must be flipped. The last calculation comes from the fact that there are P[N] - P[x] ones in the later segment of length N-x, but we want the number of zeros.
Algorithm
For example, with
S = "010110": we have P = [0, 0, 1, 1, 2, 3, 3]. Now say we want to evaluate having x=3 zeros.
There are
P[3] = 1 ones in the first 3 characters, and P[6] - P[3] = 2 ones in the later N-x = 3characters.
So, there is
(N-x) - (P[N] - P[x]) = 1 zero in the later N-x characters.
We take the minimum among all candidate answers to arrive at the final answer.
public int minFlipsMonoIncr(String S) {
int N = S.length();
int[] P = new int[N + 1];
for (int i = 0; i < N; ++i)
P[i + 1] = P[i] + (S.charAt(i) == '1' ? 1 : 0);
int ans = Integer.MAX_VALUE;
for (int j = 0; j <= N; ++j) {
ans = Math.min(ans, P[j] + N - j - (P[N] - P[j]));
}
return ans;
}
https://www.cnblogs.com/seyjs/p/9828593.html
转换后的字符串有两种形式,一个是全为0,另一个是前半部分全是0后半部分全是1。第一种情况的翻转次数是S中1的个数;第二种的情况,我们只要找出转换后的字符串第一个1所在的位置即可。设第一个所在的位置是i,那么S[0:i-1]区间内所有1都要变成0,而S[i:-1]区间内所有的0要变成1,总的翻转次数就是前一段区间内1的个数加上后一段区间内0的个数即可。遍历S,即可求出第二种情况的最小值,再与第一种情况求得的值比较取最小值即可。
def minFlipsMonoIncr(self, S): """ :type S: str :rtype: int """ t_count_1 = S.count('1') t_count_0 = len(S) - t_count_1 res = t_count_1 count_0 = 0 count_1 = 0 for i,v in enumerate(S): if v == '0': count_0 += 1 else: #count_1 += 1 # if convert this 1 to 0 res = min(res,count_1 + (t_count_0 - count_0)) count_1 += 1 return reshttps://leetcode.com/problems/flip-string-to-monotone-increasing/discuss/183896/Prefix-Suffix-Java-O(N)-One-Pass-Solution-Space-O(1)
This is a typical case of DP.
Let's see the sub-question of DP first.
Suppose that you have a string
s, and the solution to the mono increase question is already solved. That is, for string s, counter_flip flips are required for the string, and there were counter_one '1's in the original string s.
Let's see the next step of DP.
Within the string
s, a new incoming character, say ch, is appended to the original string. The question is that, how should counter_flip be updated, based on the sub-question? We should discuss it case by case.- When
'1'comes, no more flip should be applied, since'1'is appended to the tail of the original string. - When
'0'comes, things become a little bit complicated. There are two options for us: flip the newly appended'0'to'1', aftercounter_flipflips for the original string; or flipcounter_one'1'in the original string to'0'. Hence, the result of the next step of DP, in the'0'case, isstd::min(counter_flip + 1, counter_one);.
int minFlipsMonoIncr(const std::string& S, int counter_one = 0, int counter_flip = 0) {
for (auto ch : S) {
if (ch == '1') {
++counter_one;
} else {
++counter_flip;
}
counter_flip = std::min(counter_one, counter_flip);
}
return counter_flip;
}
We need to split the array into left '0' and right '1' sub-arrays, so that sum of '1' -> '0' flips (left) and '0' -> '1' flips (right) is minimal.
- Count of '0' -> '1' flips going left to right, and store it in
f0. - Count of '1' -> '0' flips going right to left, and store it in
f1. - Find a the smallest
f0[i] + f1[i].
int minFlipsMonoIncr(string S) {
vector<int> f0(S.size() + 1), f1(S.size() + 1);
int res = INT_MAX;
for (auto i = 0; i < S.size(); ++i) {
f0[i + 1] += f0[i] + (S[i] == '0' ? 0 : 1);
f1[S.size() - i - 1] += f1[S.size() - i] + (S[S.size() - i - 1] == '0' ? 1 : 0);
}
for (auto i = 0; i <= S.size(); ++i) res = min(res, f0[i] + f1[i]);
return res;
}
Actually, this problem look similar to 122. Best Time to Buy and Sell Stock III. Now with this intuition, can we do better and save some memory?
We can go left to right, and virtually 'move' the split point every time we see that we need less '0' -> '1' than '1' -> '0' flips (
We can go left to right, and virtually 'move' the split point every time we see that we need less '0' -> '1' than '1' -> '0' flips (
f1 = min(f0, f1 + 1 - (c - '0'))).int minFlipsMonoIncr(string S, int f0 = 0, int f1 = 0) {
for (auto c : S) {
f0 += c - '0';
f1 = min(f0, f1 + 1 - (c - '0'));
}
return f1;
}
leftOne[i] represents count of 1s in S[0...i]rightZero[i] represents count of 0s in S[i...n-1]Then
min = min(leftOne[i] + rightZero[i + 1]), where i = 0, ... n-1 public int minFlipsMonoIncr(String S) {
int n = S.length();
int[] leftOne = new int[n];
int[] rightZero = new int[n];
if (S.charAt(0) == '1') {
leftOne[0] = 1;
}
if (S.charAt(n - 1) == '0') {
rightZero[n - 1] = 1;
}
for (int i = 1; i < n; i++) {
leftOne[i] = S.charAt(i) == '1' ? leftOne[i - 1] + 1 : leftOne[i - 1];
rightZero[n - 1 - i] = S.charAt(n - 1 - i) == '0' ? rightZero[n - i] + 1 : rightZero[n - i];
}
int min = n;
for (int i = -1; i < n; i++) {
int left = i == -1 ? 0 : leftOne[i];
int right = i == n - 1 ? 0 : rightZero[i + 1];
min = Math.min(min, left + right);
}
return min;
}
X. https://zhanghuimeng.github.io/post/leetcode-926-flip-string-to-monotone-increasing/
一个立即可以想到的思路是枚举。枚举每一位作为1的起始点,然后根据这一位左边的1的个数和右边的0的个数算出总的翻转次数,然后取最小值。前缀中1的个数和后缀中0的个数都很好维护。
另一个相当神奇的思路[1]应用了贪心法。在从左向右扫描的过程中,我们动态维护这个分割点,分割点左侧1的数量,分割点右侧1的数量和0的数量;一旦发现分割点右侧0的数量超过了1的数量,说明此时把分割点直接右移到当前扫描点可以减小翻转次数。举个例子:
S = "00011000"i | virtual split point | left 1 cnt | right 0 cnt | right 1 cnt |
|---|---|---|---|---|
| 0 | 0 (| 00011000) | 0 | 0 | 0 |
| 1 | 1 (0| 0011000) | 0 | 0 | 0 |
| 2 | 2 (00| 011000) | 0 | 0 | 0 |
| 3 | 3 (000| 11000) | 0 | 0 | 0 |
| 4 | 3 (000|1 1000) | 0 | 0 | 1 |
| 5 | 3 (000|11 000) | 0 | 0 | 2 |
| 6 | 3 (000|110 00) | 0 | 1 | 2 |
| 7 | 3 (000|1100 0) | 0 | 2 | 2 |
| 8 | 8 (00011000|) | 2 | 0 | 0 |
这个算法的正确性怎么证明……好吧,懒得去想了。大概应该用反证法。
int minFlipsMonoIncr(string S) { int leftOnes = 0, rightOnes = 0, rightZeros = 0; for (int i = 0; i < S.size(); i++) { if (S[i] == '0') rightZeros++; else rightOnes++; if (rightZeros > rightOnes) { // move split point to i leftOnes += rightOnes; rightOnes = rightZeros = 0; } } return leftOnes + rightZeros; }https://leetcode.com/problems/flip-string-to-monotone-increasing/discuss/183851/C++-4-lines-O%28n%29-or-O%281%29-DP
We need to split the array into left '0' and right '1' sub-arrays, so that sum of '1' -> '0' flips (left) and '0' -> '1' flips (right) is minimal.
- Count of '0' -> '1' flips going left to right, and store it in
f0. - Count of '1' -> '0' flips going right to left, and store it in
f1. - Find a the smallest
f0[i] + f1[i].
int minFlipsMonoIncr(string S, int res = INT_MAX) {
vector<int> f0(S.size() + 1), f1(S.size() + 1);
for (int i = 1, j = S.size() - 1; j >= 0; ++i, --j) {
f0[i] += f0[i - 1] + (S[i - 1] == '0' ? 0 : 1);
f1[j] += f1[j + 1] + (S[j] == '1' ? 0 : 1);
}
for (int i = 0; i <= S.size(); ++i) res = min(res, f0[i] + f1[i]);
return res;
}

This reminds me of 122. Best Time to Buy and Sell Stock III. That problem has a DP solution with O(1) memory complexity, so we can try to apply it here. We can go left to right, and virtually 'move' the split point every time we see that we need less '0' -> '1' than '1' -> '0' flips (
f1 = min(f0, f1 + 1 - (c - '0'))).int minFlipsMonoIncr(string S, int f0 = 0, int f1 = 0) {
for (auto c : S) {
f0 += c - '0';
f1 = min(f0, f1 + 1 - (c - '0'));
}
return f1;
}
Here is Java version. Note that I am using
charAt(i) instead of toCharArray() to keep the memory complexity a constant.public int minFlipsMonoIncr(String S) {
int f0 = 0, f1 = 0;
for (int i = 0; i < S.length(); ++i) {
f0 += S.charAt(i) - '0';
f1 = Math.min(f0, f1 + 1 - (S.charAt(i) - '0'));
}
return f1;
}