LeetCode 924 - Minimize Malware Spread

Related:
LeetCode 924 - Minimize Malware Spread
LeetCode 928 - Minimize Malware Spread II
https://leetcode.com/problems/minimize-malware-spread/

In a network of nodes, each node i is directly connected to another node j if and only if graph[i][j] = 1.

Some nodes initial are initially infected by malware.  Whenever two nodes are directly connected and at least one of those two nodes is infected by malware, both nodes will be infected by malware.  This spread of malware will continue until no more nodes can be infected in this manner.

Suppose M(initial) is the final number of nodes infected with malware in the entire network, after the spread of malware stops.

We will remove one node from the initial list.  Return the node that if removed, would minimize M(initial).  If multiple nodes could be removed to minimize M(initial), return such a node with the smallest index.

Note that if a node was removed from the initial list of infected nodes, it may still be infected later as a result of the malware spread.

Example 1:

Input: graph = [[1,1,0],[1,1,0],[0,0,1]], initial = [0,1]
Output: 0

https://buptwc.github.io/2018/10/15/Leetcode-924-Minimize-Malware-Spread/

假设图结构如下图所示，初始感染节点为[1,3,5]，由黄色节点表示:

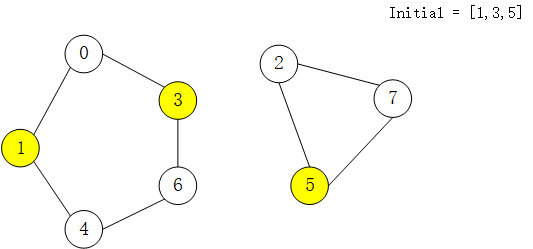
如果我们什么不操作，那么最终图上所有的节点都会被感染。
那我们现在想删一个初始感染节点，应该怎么去选呢？
假设删除1，最终左边这个连通子图还是会全部被感染，因为3是感染节点
删除3同删除1
假设删除5,可以使右边这个连通子图的所有节点不被感染，成功使感染节点少了3个

我们很容易发现，如果在一个连通子图里面，有两个或两个以上的节点初始被感染，那么无论我们删除哪个都对最后结果没有影响。我们唯一能使感染节点减少的操作就是删除那些只有一个感染节点的连通子图中的感染节点。

所以整个代码的逻辑应该如下：

1. 找到一个连通子图
2. 判断子图中感染节点的数量，若为1，执行第三步；反之执行第一步
3. 计算该子图的长度，长度越长，就越可以最小化感染节点的数量

Approach 2: Union-Find
https://www.happygirlzt.com/2018/12/14/924-minimize-malware-spread-explaination-and-solution/

As stated before, we can solve this problem by using disjoint set data structures, which have union and find methods. Why? Because we have to know the connections of the nodes. If there are two or more nodes infected and they are all connected, even if we remove it, it will not make any difference. So, we should spread these nodes into disjoint sets and a little difference from the common disjoint sets is that we should know the size of each sets. Do not forget to initialize the roots array and the counts array, as each set initially has 1 node and each node is his own root.

Ok, then, we use a HashMap to save the infected nodes in each set. How? We iterate the initial array, and to each infected node, we find its root, and make the recorded infected ++. In this way, we can know how many nodes are infected in each set.

We have to sort the initial array, the reason is that if we do not have any sets with only 1 infected node, we should return the infected with minimum index.

The last step is we iterate the initial array again. We should keep three varibles, the first one is the final result, the second one is the size of the set of the current infected node belong to, the last one is the maximum set size.
This time, we check if there is only one infected node in the set, if is, we compare the current set size with the global maximum size, if the set size is larger than the maximum size, the result is the current node; otherwise, simply return the first infected node.

    class DSU {
       int[] roots;
       int[] counts;

       public DSU(int n) {
           counts = new int[n];
           roots = new int[n];
           Arrays.fill(counts, 1);
           for (int i = 0; i < n; i++) {
               roots[i] = i;
           }
       }

       public int find(int i) {
           if (roots[i] != i) {
               roots[i] = find(roots[i]);
           }

           return roots[i];
       }

       public void union(int x, int y) {
           int rx = find(x), ry = find(y);
           if (rx == ry) return;
           roots[ry] = rx;
           counts[rx] += counts[ry];
       }

       public int size(int i) {
           // remember to find its root
            return counts[find(i)];
        }
    }

    public int minMalwareSpread(int[][] graph, int[] initial) {
        if (graph == null || graph.length == 0) return 0;
         int n = graph.length;

         DSU dsu = new DSU(n);
         for (int i = 0; i < n; i++) {
             for (int j = 0; j < n; j++) {
                 if (graph[i][j] == 1) {
                      dsu.union(i, j);
                  }
              }
         }

         Arrays.sort(initial);

         Map<Integer, Integer> map = new HashMap<>();
        // save the total number of infected points in each set
        for (int i : initial) {
             int root = dsu.find(i);
             map.put(root, map.getOrDefault(root, 0) + 1);
        }

        // compare the size of the set
        int res = -1, maxSize = -1;
        for (int i : initial) {
            int root = dsu.find(i);
            int size = 0;
            //System.out.println(size);
            // there is only one infected point
            if (map.get(root) == 1) {
                size = dsu.size(root);
               // System.out.println("Hello");
            }

            if (size > maxSize) {
                res = i;
                maxSize = size;
                //System.out.println(res);
            }
        }

        return res;
    }

As in Approach 1, it is clear that we will need to consider components of the graph. A "Disjoint Set Union" (DSU) data structure is ideal for this.

We will skip the explanation of how a DSU structure is implemented. Please refer to https://leetcode.com/problems/redundant-connection/solution/ for a tutorial on DSU.

To our DSU, we can keep a side count of the size of each component. Whenever we union two components together, the size of those components are added.

With these details neatly handled by our DSU structure, we can continue in a similar manner to Approach 1: for each node in initial with a unique color, we will consider it as a candidate answer. If no node in initialhave a unique color, then we will take min(initial) as the answer.

Note that for brevity, our DSU implementation does not use union-by-rank. This makes the asymptotic time complexity larger.

• Time Complexity: $O(N^2)$, where $N$ is the length of graph, as the graph is given in adjacent matrix form.
• Space Complexity: $O(N)$. 

  public int minMalwareSpread(int[][] graph, int[] initial) {

    int N = graph.length;

    DSU dsu = new DSU(N);

    for (int i = 0; i < N; ++i)

      for (int j = i + 1; j < N; ++j)

        if (graph[i][j] == 1)

          dsu.union(i, j);

    int[] count = new int[N];

    for (int node : initial)

      count[dsu.find(node)]++;

    int ans = -1, ansSize = -1;

    for (int node : initial) {

      int root = dsu.find(node);

      if (count[root] == 1) { // unique color

        int rootSize = dsu.size(root);

        if (rootSize > ansSize) {

          ansSize = rootSize;

          ans = node;

        } else if (rootSize == ansSize && node < ans) {

          ansSize = rootSize;

          ans = node;

        }

      }

    }

    if (ans == -1) {

      ans = Integer.MAX_VALUE;

      for (int node : initial)

        ans = Math.min(ans, node);

    }

    return ans;

  }

}

class DSU {

  int[] p, sz;

  DSU(int N) {

    p = new int[N];

    for (int x = 0; x < N; ++x)

      p[x] = x;

    sz = new int[N];

    Arrays.fill(sz, 1);

  }

  public int find(int x) {

    if (p[x] != x)

      p[x] = find(p[x]);

    return p[x];

  }

  public void union(int x, int y) {

    int xr = find(x);

    int yr = find(y);

    p[xr] = yr;

    sz[yr] += sz[xr];

  }

  public int size(int x) {

    return sz[find(x)];

  }

Approach 1: Depth First Search

First, let's color (the nodes of) each component of the graph. We can do this using a depth first search.

Afterwards, notice that if two nodes in initial have the same color (ie., belong to the same component), then removing them from initial won't decrease M(initial). This is because the malware will spread to reach every node in this component no matter what.

So, among nodes with a unique color in initial, we will remove the node with the largest component size. (If there's a tie, we return the smallest index. Also, if there aren't any nodes with a unique color, we'll just return the smallest index node.)

Algorithm

This algorithm has a few parts:

• Coloring each component: For each node, if it isn't yet colored, use a depth-first search to traverse its component, coloring that component with a new color.
• Size of each color: Count the number of occurrences of each color.
• Find unique colors: Look at the colors of nodes in initial to see which nodes have unique colors.
• Choose answer: For each node with a unique color, find the size of that color. The largest size is selected, with ties broken by lowest node number.
  • If there is no node with a unique color, the answer is min(initial).

• Time Complexity: $O(N^2)$, where $N$ is the length of graph, as the graph is given in adjacent matrix form.
• Space Complexity: $O(N)$. 

  public int minMalwareSpread(int[][] graph, int[] initial) {

    // 1. Color each component.

    // colors[node] = the color of this node.

    int N = graph.length;

    int[] colors = new int[N];

    Arrays.fill(colors, -1);

    int C = 0;

    for (int node = 0; node < N; ++node)

      if (colors[node] == -1)

        dfs(graph, colors, node, C++);

    // 2. Size of each color.

    int[] size = new int[C];

    for (int color : colors)

      size[color]++;

    // 3. Find unique colors.

    int[] colorCount = new int[C];

    for (int node : initial)

      colorCount[colors[node]]++;

    // 4. Answer

    int ans = Integer.MAX_VALUE;

    for (int node : initial) {

      int c = colors[node];

      if (colorCount[c] == 1) {

        if (ans == Integer.MAX_VALUE)

          ans = node;

        else if (size[c] > size[colors[ans]])

          ans = node;

        else if (size[c] == size[colors[ans]] && node < ans)

          ans = node;

      }

    }

    if (ans == Integer.MAX_VALUE)

      for (int node : initial)

        ans = Math.min(ans, node);

    return ans;

  }

  public void dfs(int[][] graph, int[] colors, int node, int color) {

    colors[node] = color;

    for (int nei = 0; nei < graph.length; ++nei)

      if (graph[node][nei] == 1 && colors[nei] == -1)

        dfs(graph, colors, nei, color);

  }

https://www.hrwhisper.me/leetcode-contest-106-solution/

上面的方法可以进行优化：假如a能到b，由于是无向图，那么b也能到达a，那么只需要先对initial数组排序，然后对没有访问的结点dfs就行了

Python

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

class Solution(object):     def dfs(self, cur, g, vis, source, cnt):         vis[cur] = True         cnt[source] += 1         for to in range(len(g[cur])):             if not g[cur][to] or vis[to]:                 continue             self.dfs(to, g, vis, source, cnt)     def minMalwareSpread(self, graph, initial):         """         :type graph: List[List[int]]         :type initial: List[int]         :rtype: int         """         cnt = [0] * len(graph)         vis = [False] * len(graph)         initial.sort()         for from_ in initial:             self.dfs(from_, graph, vis, from_, cnt)         max_node = initial[0]         for node in initial:             if cnt[node] > cnt[max_node]:                 max_node = node         return max_node

https://leetcode.com/problems/minimize-malware-spread/discuss/181100/Brute-force-or-Union-Find

    public int minMalwareSpread(int[][] graph, int[] initial) {
        int cand = -1, min = graph.length + 1, n = graph.length;
        Arrays.sort(initial);
        for (int i : initial) {
            boolean[] infected = new boolean[n];
            int count = 0;
            for (int remain : initial) {
                if (remain == i) {
                    continue;
                }
                count += malware(graph, remain, infected);
            }
            if (count < min) {
                cand = i;
                min = count;
            }
        }
        return cand;
    }
    private int malware(int[][] graph, int n, boolean[] infected) {
        if (infected[n]) {
            return 0;
        }
        int result = 1;
        infected[n] = true;
        for (int next = 0; next < graph.length; next++) {
            if (graph[n][next] == 1) {
                result += malware(graph, next, infected);
            }
        }
        return result;
    }

X. BFS 

https://www.acwing.com/solution/leetcode/content/566/

遍历去除初始点集中的每一个点，分别求最大连通分量（BFS），取最小值

(BFS) O(nm)O(nm)

枚举每一个在initial中的点，删掉它，然后用 BFS 判定一下连通性即可。

时间复杂度

枚举的时间复杂度为 O(n)O(n)，然后用 BFS 判定时间复杂度为 O(n+m)O(n+m)，故总时间复杂度为 O(nm)O(nm)。

    int minMalwareSpread(vector<vector<int>>& graph, vector<int>& initial) {

        int n = graph.size(), m = initial.size();

        int ans = n + 1, id = -1;

        sort(initial.begin(), initial.end());

        for (int block = 0; block < m; block++) {

            queue<int> q;

            vector<bool> vis(n, false);

            int tot = 0;

            for (int i = 0; i < m; i++)

                if (initial[i] != initial[block]) {

                    q.push(initial[i]);

                    vis[initial[i]] = true;

                    tot++;

                }

            while (!q.empty()) {

                int cur = q.front();

                q.pop();

                for (int i = 0; i < n; i++)

                    if (graph[cur][i] == 1 && !vis[i]) {

                        vis[i] = true;

                        q.push(i);

                        tot++;

                    }

            }

            if (ans > tot) {

                ans = tot;

                id = initial[block];

            }

        }

        return id;

    }

https://www.jianshu.com/p/cd78154ce835

    int minMalwareSpread(vector<vector<int>>& graph, vector<int>& initial) {
        sort(initial.begin(),initial.end());
        vector<int> nodes(graph.size(),1);
        vector<int> temp;
        queue<int> stacks;
        int maxv = INT_MIN;
        int maxi = INT_MIN;
        for(int i =0;i<initial.size();i++){
            if(nodes[initial[i]]!=-1){
                temp.clear();
                stacks.push(initial[i]);
                int index;
                while(!stacks.empty()){
                    index = stacks.front();
                    nodes[index] = -1;
                    temp.push_back(index);
                    stacks.pop();
                    for(int j = 0;j<graph[index].size();j++){
                        if(nodes[j]==1&&graph[index][j] == 1)
                        {   stacks.push(j);
                            nodes[j] = -1;
                        }
                    }
                }
                int c = temp.size();
                if(c > maxv) {
                    maxv = temp.size();
                    maxi = initial[i];
                }
            }
        }
        return maxi;
    }
};

https://leetcode.com/problems/minimize-malware-spread/discuss/181116/Java-BFS

BFS with a list of infected nodes. Try removing each one, if the new candidate is (a lower node number and == amount of infected) or a less amount of infected then update the resulting answer node.

    private int spread(int [][] graph, Set<Integer> infected){
        Set<Integer> bad = new HashSet<>(infected);
        Queue<Integer> bfs= new LinkedList<>();
        for(Integer initialInfected:infected){
            bfs.add(initialInfected);
        }
        while(!bfs.isEmpty()){
            Integer next = bfs.remove();
            for(int j=0; j<graph[next].length;++j){
                if(graph[next][j]==1&& !bad.contains(j)){
                    bad.add(j);
                    bfs.add(j);
                }
            }
        }
        //return how many total were infected after spreading
        return bad.size();
    }
    public int minMalwareSpread(int[][] graph, int[] initial) {
        Set<Integer> infected = new HashSet<>();
        for(int initialInfected: initial){
            infected.add(initialInfected);
        }
        int min = Integer.MAX_VALUE;
        int ans = 0;
        for(int ignore = 0; ignore<initial.length;++ignore){
            int ignoreNumb = initial[ignore];
            infected.remove(ignoreNumb);
            int amount = spread(graph,infected);
            if(amount<min ||(amount==min&& initial[ignore]<ans)){
                ans=initial[ignore];
                min=amount;
            }
            infected.add(ignoreNumb);
        }
        return ans;
    }

X. BFS
http://www.noteanddata.com/leetcode-924-Minimize-Malware-Spread.html