LeetCode 878 - Nth Magical Number

https://leetcode.com/problems/nth-magical-number/

A positive integer is magical if it is divisible by either A or B.

Return the N-th magical number.  Since the answer may be very large, return it modulo 10^9 + 7.

Example 1:

Input: N = 1, A = 2, B = 3
Output: 2

Example 2:

Input: N = 4, A = 2, B = 3
Output: 6

Example 3:

Input: N = 5, A = 2, B = 4
Output: 10

Example 4:

Input: N = 3, A = 6, B = 4
Output: 8

Note:

1. 1 <= N <= 10^9
2. 2 <= A <= 40000
3. 2 <= B <= 40000

https://blog.csdn.net/XX_123_1_RJ/article/details/81476088
这个题目，应该有一半是数学问题，不易想到。先简单介绍一下容斥原理，我们要求两个集合的并集，可以先把两个单集合相加，然后减去他们的交集就可以（网上有大把，可以参考哦，这里只是简单一提）。
（1）返回第 N 个神奇数字？很显然，这个神奇数字里面应该包含N个数字可以被 A 或 B 整除（这里的包含可以理解为神奇数字前面的数字，不太严谨哈）。
（2）现在，我们可以设置两个界限，一个最小下界 0，一个最大上界10**15。
（3）在两个上下界限内，进行二分查找，看看哪数字合适。
（4）如何确定这个神奇数字包含的个数？有数学方法可以求出来，简单理解就是求出这个神奇数字的能被A整除的个数+被B整除的个数-能同时被A、B整除的个数 （也就用到容斥原理，具体的可以去网上深入学习哦），即可。
https://zxi.mytechroad.com/blog/math/leetcode-878-nth-magical-number/

Let n denote the number of numbers <= X that are divisible by either A or B.

n = X / A + X / B – X / lcm(A, B) = X / A + X / B – X / (A * B / gcd(A, B))

Binary search for the smallest X such that n >= N

http://tashi711.xyz/programming/reports/leetcode/leetcode-878/

　　第一反应就是二分答案，判定一个数x内有多少个Magical Number很容易，稍微容斥一下，即

⌊xA+xB−xlcm(A,B)⌋$$\lfloor \frac{x}{A}+\frac{x}{B}-\frac{x}{lcm(A,B)}\rfloor$$

　　只需要二分N∗min(A,B)$N\ast min(A,B)$内的数即可，因为必有N个A或B。
　　其实之后才想到官方题解中复杂度更高的那个算法，也就是在每lcm(A, B)个数出现的Magical Number模式（个数）是一样的，因此可以看看lcm(A, B)内有多少个，然后取个模，枚举剩下的。

 int gcd(int u, int v) {
  if (v == 0) {
   return u;
  }
  return gcd(v, u % v);
 }

 int nthMagicalNumber(int N, int A, int B) {
  long long u = 0, v = static_cast<long long>(N) * min(A, B);
  int lcm = A / gcd(A, B) * B;
  while (u < v) {
   long long m = u + (v - u) / 2;
   if (m / A + m / B - m / lcm < N) {
    u = m + 1;
   }
   else {
    v = m;
   }
  }
  return u % kModule;
 }

https://www.cnblogs.com/seyjs/p/9597987.html
本题求的是第N个Magical Number，我们可以很轻松的知道这个数的取值范围 [min(A,B), N*max(A,B)]。对于知道上下界求具体数字的题目，可以考虑用二分查找。这样题目就从找出第N个Magical Number变成判断一个数是否是第N个Magical Number。假设n是其中一个Magical Number，显然n满足 n % A == 0 或者 n % B == 0。对于A来说，从A到n之间有n/A个Magical Number，而对B来说是n/B个Magical Number。但是n却并不是第（n/A + n/B）个Magical Number，因为这两者之间会有满足A * i == B * j数字出现，这样会造成重复，这样的数字有多少个呢？和A与B的最小公倍数有关，有n/LCM(A,B)个

https://leetcode.com/problems/nth-magical-number/discuss/154613/C%2B%2BJavaPython-Binary-Search

1. Get gcd (greatest common divisor) and lcm (least common multiple) of (A, B).
   (a, b) = (A, B) while b > 0: (a, b) = (b, a % b)
   then, gcd = a and lcm = A * B / a
2. How many magic numbers <= x ?
   By inclusion exclusion principle, we have:
   x / A + x / B - x / lcm
3. Set our binary search range
   Lower bound is min(A, B), I just set left = 2.
   Upper bound is N * min(A, B), I just set right = 10 ^ 14.
4. binary search, find the smallest x that x / A + x / B - x / lcm = N

    public int nthMagicalNumber(int N, int A, int B) {
        long a = A, b = B, tmp, l = 2, r = (long)1e14, mod = (long)1e9 + 7;
        while (b > 0) {
            tmp = a;
            a = b;
            b = tmp % b;
        }
        while (l < r) {
            long m = (l + r) / 2;
            if (m / A + m / B - m / (A * B / a) < N) l = m + 1;
            else r = m;
        }
        return (int)(l % mod);
    }

Approach 2: Binary Search

The number of magical numbers less than or equal to $x$ is a monotone increasing function in $x$, so we can binary search for the answer.

Algorithm

Say $L = \text{lcm}(A, B)$, the least common multiple of $A$ and $B$; and let $f(x)$ be the number of magical numbers less than or equal to $x$. A well known result says that $L = \frac{A * B}{\text{gcd}(A, B)}$, and that we can calculate the function $\gcd$. For more information on least common multiples and greatest common divisors, please visit Wikipedia - Lowest Common Multiple.

Then $f(x) = \lfloor \frac{x}{A} \rfloor + \lfloor \frac{x}{B} \rfloor - \lfloor \frac{x}{L} \rfloor$. Why? There are $\lfloor \frac{x}{A} \rfloor$ numbers $A, 2A, 3A, \cdots$ that are divisible by $A$, there are $\lfloor \frac{x}{B} \rfloor$ numbers divisible by $B$, and we need to subtract the $\lfloor \frac{x}{L} \rfloor$ numbers divisible by $A$ and $B$ that we double counted.

Finally, the answer must be between $0$ and $N * \max(A, B)$. Without loss of generality, suppose $A \geq B$, so that it remains to show

$\lfloor \frac{N * \max(A, B)}{A} \rfloor + \lfloor \frac{N * \max(A, B)}{B} \rfloor - \lfloor \frac{N * \max(A, B)}{\text{lcm}(A, B)} \rfloor \geq N$

$\Leftrightarrow \lfloor \frac{N*A}{A} \rfloor + \lfloor \frac{N*A}{B} \rfloor - \lfloor \frac{N*A*\gcd(A, B)}{A*B} \rfloor \geq N$

$\Leftrightarrow \lfloor \frac{N*A}{B} \rfloor \geq \lfloor \frac{N*\gcd(A, B)}{B} \rfloor$

$\Leftrightarrow A \geq \gcd(A, B)$

as desired.

Afterwards, the binary search on $f$ is straightforward. For more information on binary search, please visit [LeetCode Explore - Binary Search].

Time Complexity: $O(\log (N * \max(A, B)))$.

  public int nthMagicalNumber(int N, int A, int B) {

    int MOD = 1_000_000_007;

    int L = A / gcd(A, B) * B;

    long lo = 0;

    long hi = (long) 1e15;

    while (lo < hi) {

      long mi = lo + (hi - lo) / 2;

      // If there are not enough magic numbers below mi...

      if (mi / A + mi / B - mi / L < N)

        lo = mi + 1;

      else

        hi = mi;

    }

    return (int) (lo % MOD);

  }

  public int gcd(int x, int y) {

    if (x == 0)

      return y;

    return gcd(y % x, x);

  }

Approach 1: Mathematical

Let's try to count to the $N$-th magical number mathematically.

First, the pattern of magical numbers repeats. Let $L$ be the least common multiple of $A$ and $B$. If $X \leq L$ is magical, then $X + L$ is magical, because (for example) $A | X$ and $A | L$ implies $A | (X + L)$, and similarly if $B$were the divisor.

There are $M = \frac{L}{A} + \frac{L}{B} - 1$ magical numbers less than or equal to $L$: $\frac{L}{A}$ of them are divisible by $A$, $\frac{L}{B}$ of them are divisible by $B$, and $1$ of them is divisible by both. So instead of counting one at a time, we can count by $M$ at a time.

Now, suppose $N = M*q + r$ (with $r < M$). The first $L*q$ numbers contain $M*q$ magical numbers, and within the next numbers $(L*q + 1, L*q + 2, \cdots)$ we want to find $r$ more magical ones.

For this task, we can use brute force. The next magical number (less $L*q$) will either be $A$ or $B$. If for example it is $A$, then the next number will either be $2*A$ or $B$, and so on.

If the $r$-th such magical number is $Y$, then the final answer is $L*q + Y$. Care must also be taken in the case that $r$ is $0$.

Time Complexity: $O(A+B)$, assuming a model where integer math operations are $O(1)$. The calculation of q * L is $O(1)$. The calculation of the $r$-th magical number after $q*M$ is $O(M)$ which is $O(A+B)$.

  public int nthMagicalNumber(int N, int A, int B) {

    int MOD = 1_000_000_007;

    int L = A / gcd(A, B) * B;

    int M = L / A + L / B - 1;

    int q = N / M, r = N % M;

    long ans = (long) q * L % MOD;

    if (r == 0)

      return (int) ans;

    int[] heads = new int[] { A, B };

    for (int i = 0; i < r - 1; ++i) {

      if (heads[0] <= heads[1])

        heads[0] += A;

      else

        heads[1] += B;

    }

    ans += Math.min(heads[0], heads[1]);

    return (int) (ans % MOD);

  }

  public int gcd(int x, int y) {

    if (x == 0)

      return y;

    return gcd(y % x, x);

  }

https://leetcode.com/problems/nth-magical-number/discuss/154965/o(1)-Mathematical-Solution-without-binary-or-brute-force-search

I have seen most of the solutions contain binary search or brute force search. Actually we can solve it with pure math solution.
First we need to find count of the LCM blocks as each LCM block contains fixed number of magic numbers. For the remain part, instead of using brute force or binary search. Actually there's linear relationship between count of magic number (F(x)) and the number (x) in following formular:
f(x) = floor(x/A) + floor(x/B)
As within an LCD block, there's no overlapping between x/A and x/B.

If we plot this in a chart, it's very close to linear furmular:
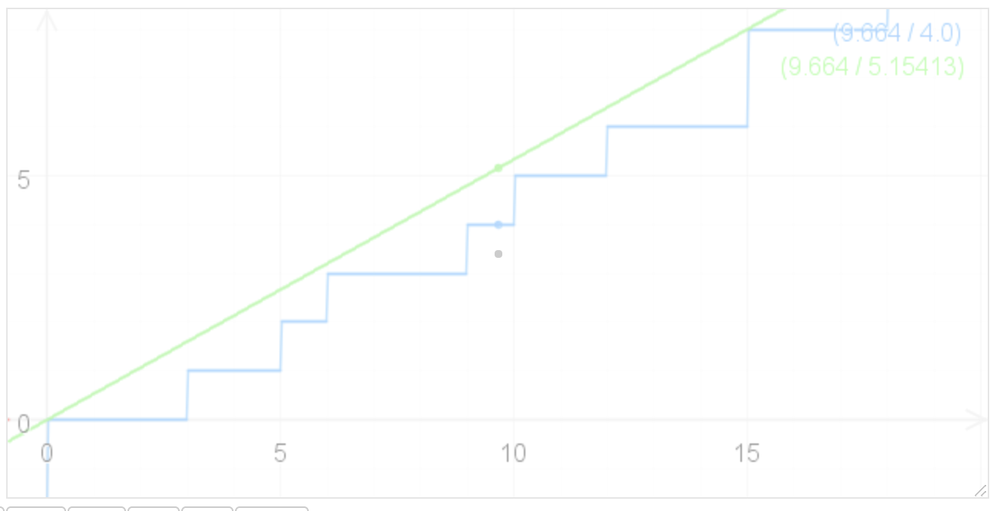
f(x) = x/A + x/B.
But it's always below this line.
following is the chart exmple for A=3, B=5

So solution to get the number within an LCM block is very simple:
The minimum integer number great than: N / ( 1/A + 1 /B ), that can be divided either by A or B.

import static java.lang.Math.ceil;
import static java.lang.Math.min;

class Solution {
 public int nthMagicalNumber(int N, int A, int B) {
    int MOD = 1_000_000_007;
    long lcm = A * B / gcd(A, B);
    long cntPerLcm = lcm / A + lcm / B - 1;
    long cntLcm = N / cntPerLcm;
    long remain = N % cntPerLcm;
    
    double nearest = remain / (1./A + 1./B);
    int remainIdx = (int)min(ceil(nearest / A) * A, ceil(nearest / B) * B);
    return (int)((cntLcm * lcm + remainIdx) % MOD);
  }
  
  public static int gcd(int A, int B) {
    return B == 0 ? A : gcd(B, A % B);
  }




Approach 1: Mathematical
https://zihan.me/2018/08/03/LeetCode-878-Nth-Magic-Number/

假设两个数的最小公倍数$L = LCM(A, B)$, 那么对于[1, L]这个区间里的数, 能被A整除的有$\lfloor \frac{L}{A} \rfloor$, 能被B整数的有$\lfloor \frac{L}{B} \rfloor$, 这两部分除了L之外不会有重合的, 因为L是最小公倍数, 因此在$[1, L]$这个区间内有$M = \lfloor \frac{L}{A} \rfloor + \lfloor \frac{L}{B} \rfloor - 1$。

而$[L + 1, 2L]$这段区间中的magic number数目和第一段区间是一样的, 所以至少有$\lfloor \frac{min(A, B)}{L} \rfloor$个 magic number。但是最后还有一小段余数, 这一段直接暴力一个一个判断就好了, 反正最多不超过L个。

代码如下, gcd可以用辗转相除法得到, 然后$lcm = \frac{A \times B}{gcd(A, B)}$

Let's try to count to the $N$-th magical number mathematically.

First, the pattern of magical numbers repeats. Let $L$ be the least common multiple of $A$ and $B$. If $X \leq L$is magical, then $X + L$ is magical, because (for example) $A \| X$ and $A \| L$ implies $A \| (X + L)$, and similarly if $B$ were the divisor.

There are $M = \frac{L}{A} + \frac{L}{B} - 1$ magical numbers less than or equal to $L$: $\frac{L}{A}$ of them are divisible by $A$, $\frac{L}{B}$ of them are divisible by $B$, and $1$ of them is divisible by both. So instead of counting one at a time, we can count by $M$ at a time.

Now, suppose $N = M*q + r$ (with $r &lt; M$). The first $L*q$ numbers contain $M*q$ magical numbers, and within the next numbers $(L*q + 1, L*q + 2, \cdots)$ we want to find $r$ more magical ones.

For this task, we can use brute force. The next magical number (less $L*q$) will either be $A$ or $B$. If for example it is $A$, then the next number will either be $2*A$ or $B$, and so on.

If the $r$-th such magical number is $Y$, then the final answer is $L*q + Y$. Care must also be taken in the case that $r$ is $0$.

Time Complexity: $O(A+B)$, assuming a model where integer math operations are $O(1)$. The calculation of q * L is $O(1)$. The calculation of the $r$-th magical number after $q*M$ is $O(M)$which is $O(A+B)$.

  public int nthMagicalNumber(int N, int A, int B) {

    int MOD = 1_000_000_007;

    int L = A / gcd(A, B) * B;

    int M = L / A + L / B - 1;

    int q = N / M, r = N % M;

    long ans = (long) q * L % MOD;

    if (r == 0)

      return (int) ans;

    int[] heads = new int[] { A, B };

    for (int i = 0; i < r - 1; ++i) {

      if (heads[0] <= heads[1])

        heads[0] += A;

      else

        heads[1] += B;

    }

    ans += Math.min(heads[0], heads[1]);

    return (int) (ans % MOD);

  }

  public int gcd(int x, int y) {

    if (x == 0)

      return y;

    return gcd(y % x, x);

  }