https://leetcode.com/problems/implement-rand10-using-rand7/
Given a function
http://hehejun.blogspot.com/2018/07/leetcodeimplement-rand10-using-rand7.html
我们先思考如何用更大的randX()实现更小的randY(),有两种情况:
http://www.cnblogs.com/grandyang/p/9727206.html
https://leetcode.com/articles/implement-rand10-using-rand7/

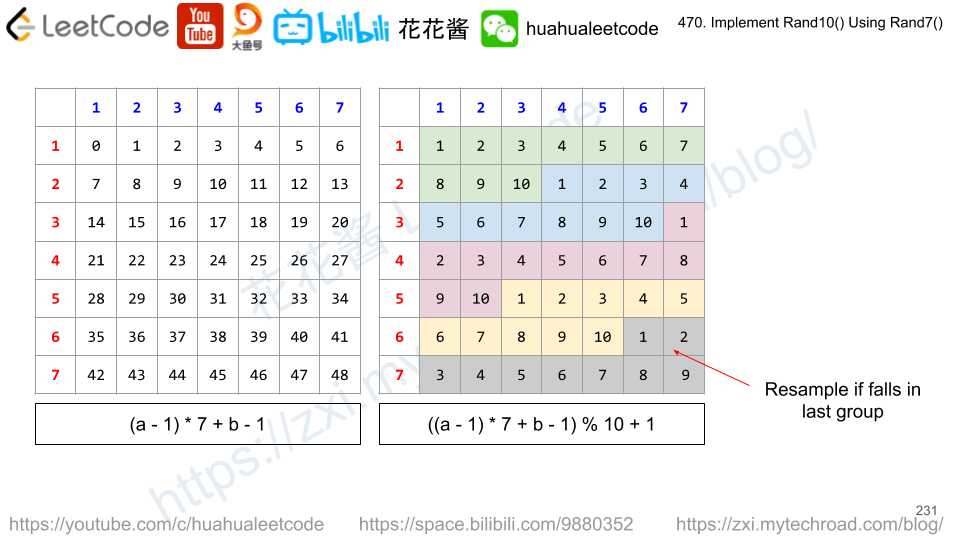
A table is used to illustrate the concept of rejection sampling. Calling rand7() twice will get us row and column index that corresponds to a unique position in the table above. Imagine that you are choosing a number randomly from the table above. If you hit a number, you return that number immediately. If you hit a * , you repeat the process again until you hit a number.
https://blog.csdn.net/wlhwaii/article/details/81108154
http://hehejun.blogspot.com/2018/07/leetcodeimplement-rand10-using-rand7.html
X.
我们还可以对上面的解法进行一下优化,因为说实话在 [1, 49] 的范围内随机到 [41, 49] 内的数字概率还是挺高的,我们可以做进一步的处理,就是当循环到这九个数字的时候,我们不重新采样,而是做进一步的处理,我们将采样到的数字减去40,这样就相当于有了个 rand9(),那么我们通过 (rand9() - 1) * 7 + rand7(),可以变成rand63(),对 rand63() 进行拒绝采样,得到 rand60(),从而又可以得到 rand10()了,此时还会多余出3个数字,[61, 63],我们通过减去60,得到 rand3(),再通过变换 (rand3() - 1) * 7 + rand7() 得到 rand21(),此时再次调用拒绝采样,得到 rand20(),进而得到 rand10(),此时就只多余出一个21,重复整个循环的概率就变的很小了
Approach 2: Utilizing out-of-range samples
Given a function
rand7 which generates a uniform random integer in the range 1 to 7, write a function rand10 which generates a uniform random integer in the range 1 to 10.
Do NOT use system's
Math.random().
Example 1:
Input: 1 Output: [7]
Example 2:
Input: 2 Output: [8,4]
Example 3:
Input: 3 Output: [8,1,10]
Note:
rand7is predefined.- Each testcase has one argument:
n, the number of times thatrand10is called.
Follow up:
- What is the expected value for the number of calls to
rand7()function? - Could you minimize the number of calls to
rand7()?
我们先思考如何用更大的randX()实现更小的randY(),有两种情况:
- 如果X % Y == 0,那么我们直接randX() % Y + 1即可。比如rand12()和rand4(),因为是整除的,所以取余之后不会改变原本的uniform distribution。
- 如果X % Y != 0,显然取余就是不行的了。比兔rand10()和rand7(),结果为1,2,3的概率就被提高了。所以我们一直call rand10()直到结果是在[1, 7]的范围之内,这样可以保证每个数字的概率仍然是uniformly distributed。
那么如果我们反过来,用更小的randY()实现更大的randX()的话。我们就要首先实现比X更大的randZ(),然后通过randZ()实现randX()。显然我们不能单纯的rand7() + rand7()或者rand7() * rand7(),这样不能保证结果是uniformly distributed的。考虑到每次generate的数字在[1, 7]范围内,减1就是[0, 6]。那么就是7进制,我们用这组基就可以构建均匀分布的更大的十进制的数,Z = (rand7() - 1) * 7 + rand7() - 1,这个就是在[0,48]范围内平均分布的随机数。我们用rand48()按照上面的方法构建rand10()即可。为了减小rand7()被call的次数,我们先构建rand40(),rand40()到rand10()的操作用简单的取余即可实现。因为每次有40/48的概率落在[0, 39]的范围内,generate符合要求的数的期望的次数为48 / 40。所以时间复杂度为O(1)。
X. Approach 1: Rejection Samplinghttp://www.cnblogs.com/grandyang/p/9727206.html
这道题给了我们一个随机生成 [1, 7] 内数字的函数rand7(),让我们利用其来生成一个能随机生成 [1, 10] 内数字的函数rand10(),注意这里的随机生成的意思是等概率生成范围内的数字。这是一道很有意思的题目,由于rand7()只能生成1到7之间的数字,所以8,9,10这三个没法生成,那么怎么办?大多数人可能第一个想法就是,再用一个呗,然后把两次的结果加起来,范围不就扩大了么,扩大成了 [2, 14] 之间,然后我们如果再减去1,范围不就是[1, 13]了么。想法不错,但是有个问题,这个范围内的每个数字生成的概率不是都相等的,为啥这么说呢,我们来举个简单的例子看下,就比如说rand2(),那么我们知道其可以生成两个数字1和2,且每个的概率都是1/2。那么对于 (rand2() - 1) + rand2()呢,我们看一下:
rand2() - 1 + rand()2 = ? 1 1 1 1 2 2 2 1 2 2 2 3
我们发现,生成数字范围 [1, 3] 之间的数字并不是等概率大,其中2出现的概率为1/2,1和3分别为1/4。那么这就不随机了。问题出在哪里了呢,如果直接相加,那么不同组合可能会产生相同的数字,比如 1+2 和 2+1 都是3。所以我们需要给第一个rand2() 升一个维度,让其乘上一个数字,再相加。比如对于 (rand2() - 1) * 2 + rand2(),如下:
(rand2() - 1) * 2 + rand()2 = ? 1 1 1 1 2 2 2 1 3 2 2 4
这时右边生成的1,2,3,4就是等概率出现的了。这样我们就通过使用rand2(),来生成rand4()了。那么反过来想一下,我们可以通过rand4()来生成rand2(),其实更加简单,我们只需通过 rand4() % 2 + 1 即可,如下:
rand4() % 2 + 1 = ? 1 2 2 1 3 2 4 1
同理,我们也可以通过 rand6() 来生成 rand2(),我们只需通过 rand6() % 2 + 1 即可,如下:
rand6() % 2 + 1 = ? 1 2 2 1 3 2 4 1 5 2 6 1
所以,回到这道题,我们可以先凑出 rand10*N(),然后再通过 rand10*N() % 10 + 1 来获得rand10()。那么,我们只需要将rand7()转化为rand10*N()即可,根据前面的讲解,我们转化也必须要保持等概率,那么就可以变化为 (rand7() - 1) * 7 + rand7(),就转为了 rand49()。但是49不是10的倍数,不过49包括好几个10的倍数,比如40,30,20,10等。这里,我们需要把rand49() 转为 rand40(),需要用到拒绝采样Rejection Sampling,总感觉名字很奇怪,之前都没有听说过这个采样方法,刷题也是个不停学习新东西的过程呢。简单来说,这种采样方法就是随机到需要的数字就接受,不是需要的就拒绝,并重新采样,这样还能保持等概率,具体的证明这里就不讲解了,博主也不会,有兴趣的童鞋们可以去Google一下~ 这里我们直接用结论就好啦,当我们用 rand49() 生成一个 [1, 49] 范围内的随机数,如果其在 [1, 40] 范围内,我们就将其转为rand10()范围内的数字,直接对10去余并加1,返回即可。如果不是,则继续循环即可
int rand10() { while (true) { int num = (rand7() - 1) * 7 + rand7(); if (num <= 40) return num % 10 + 1; } }
我们可以不用while循环,而采用调用递归函数,从而两行就搞定,叼不叼~
int rand10() { int num = (rand7() - 1) * 7 + rand7(); return (num <= 40) ? (num % 10 + 1) : rand10(); }
范围在1~7的随机数产生器,即1~7各个数字出现的概率皆为1/7.
范围在1~10的随机数产生器,即1~10各个数字出现的概率皆为1/10.
这个题的构造思路是先构造一个randN,这个N必须是10的整数倍,然后randN % 10就可以得到了rand10.
所以可以从rand7先构造出rand49,再把rand49中大于等于40的都过滤掉,这样就得到了rand40,在对10取余即可。
具体一点就是:
rand7()等概率地产生1,2,3,4,5,6,7.
rand7() - 1等概率地产生[0,6].
(rand7() - 1) *7等概率地产生0, 7, 14, 21, 28, 35, 42
(rand7() - 1) * 7 + (rand7() - 1)等概率地产生[0, 48]这49个数字
如果步骤4的结果大于等于40,那么就重复步骤4,直到产生的数小于40
把步骤5的结果mod 10 再加1, 就会等概率的随机生成[1, 10]
所以过程是:
rand7 --> rand49 --> rand40 --> rand10.
其中,构造rand49的方式是:
7 * (rand7() - 1) + rand7() - 1
What if you could generate a random integer in the range 1 to 49? How would you generate a random integer in the range of 1 to 10? What would you do if the generated number is in the desired range? What if it is not?
Algorithm
This solution is based upon Rejection Sampling. The main idea is when you generate a number in the desired range, output that number immediately. If the number is out of the desired range, reject it and re-sample again. As each number in the desired range has the same probability of being chosen, a uniform distribution is produced.
Obviously, we have to run rand7() function at least twice, as there are not enough numbers in the range of 1 to 10. By running rand7() twice, we can get integers from 1 to 49 uniformly. Why?

A table is used to illustrate the concept of rejection sampling. Calling rand7() twice will get us row and column index that corresponds to a unique position in the table above. Imagine that you are choosing a number randomly from the table above. If you hit a number, you return that number immediately. If you hit a * , you repeat the process again until you hit a number.
Since 49 is not a multiple of 10, we have to use rejection sampling. Our desired range is integers from 1 to 40, which we can return the answer immediately. If not (the integer falls between 41 to 49), we reject it and repeat the whole process again.
public int rand10() {
int row, col, idx;
do {
row = rand7();
col = rand7();
idx = col + (row - 1) * 7;
} while (idx > 40);
return 1 + (idx - 1) % 10;
}
The expected value for the number of calls to rand7() can be computed as follows:
http://hehejun.blogspot.com/2018/07/leetcodeimplement-rand10-using-rand7.html
X.
我们还可以对上面的解法进行一下优化,因为说实话在 [1, 49] 的范围内随机到 [41, 49] 内的数字概率还是挺高的,我们可以做进一步的处理,就是当循环到这九个数字的时候,我们不重新采样,而是做进一步的处理,我们将采样到的数字减去40,这样就相当于有了个 rand9(),那么我们通过 (rand9() - 1) * 7 + rand7(),可以变成rand63(),对 rand63() 进行拒绝采样,得到 rand60(),从而又可以得到 rand10()了,此时还会多余出3个数字,[61, 63],我们通过减去60,得到 rand3(),再通过变换 (rand3() - 1) * 7 + rand7() 得到 rand21(),此时再次调用拒绝采样,得到 rand20(),进而得到 rand10(),此时就只多余出一个21,重复整个循环的概率就变的很小了
Approach 2: Utilizing out-of-range samples
Intuition
There are a total of 2.45 calls to rand7() on average when using approach 1. Can we do better? Glad that you asked. In fact, we are able to improve average number of calls to rand7() by about 10%.
The idea is that we should not throw away the out-of-range samples, but instead use them to increase our chances of finding an in-range sample on the successive call to rand7.
Algorithm
Start by generating a random integer in the range 1 to 49 using the aforementioned method. In the event that we could not generate a number in the desired range (1 to 40), it is equally likely that each number of 41 to 49 would be chosen. In other words, we are able to obtain integers in the range of 1 to 9 uniformly. Now, run rand7() again to obtain integers in the range of 1 to 63 uniformly. Apply rejection sampling where the desired range is 1 to 60. If the generated number is in the desired range (1 to 60), we return the number. If it is not (61 to 63), we at least obtain integers of 1 to 3 uniformly. Run rand7() again to obtain integers in the range of 1 to 21 uniformly. The desired range is 1 to 20, and in the unlikely event we get a 21, we reject it and repeat the entire process again.
public int rand10() {
int a, b, idx;
while (true) {
a = rand7();
b = rand7();
idx = b + (a - 1) * 7;
if (idx <= 40)
return 1 + (idx - 1) % 10;
a = idx - 40;
b = rand7();
// get uniform dist from 1 - 63
idx = b + (a - 1) * 7;
if (idx <= 60)
return 1 + (idx - 1) % 10;
a = idx - 60;
b = rand7();
// get uniform dist from 1 - 21
idx = b + (a - 1) * 7;
if (idx <= 20)
return 1 + (idx - 1) % 10;
}
}