LeetCode 986 - Interval List Intersections

https://leetcode.com/problems/interval-list-intersections/

Given two lists of closed intervals, each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

(Formally, a closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b.  The intersection of two closed intervals is a set of real numbers that is either empty, or can be represented as a closed interval.  For example, the intersection of [1, 3] and [2, 4] is [2, 3].)

Example 1:

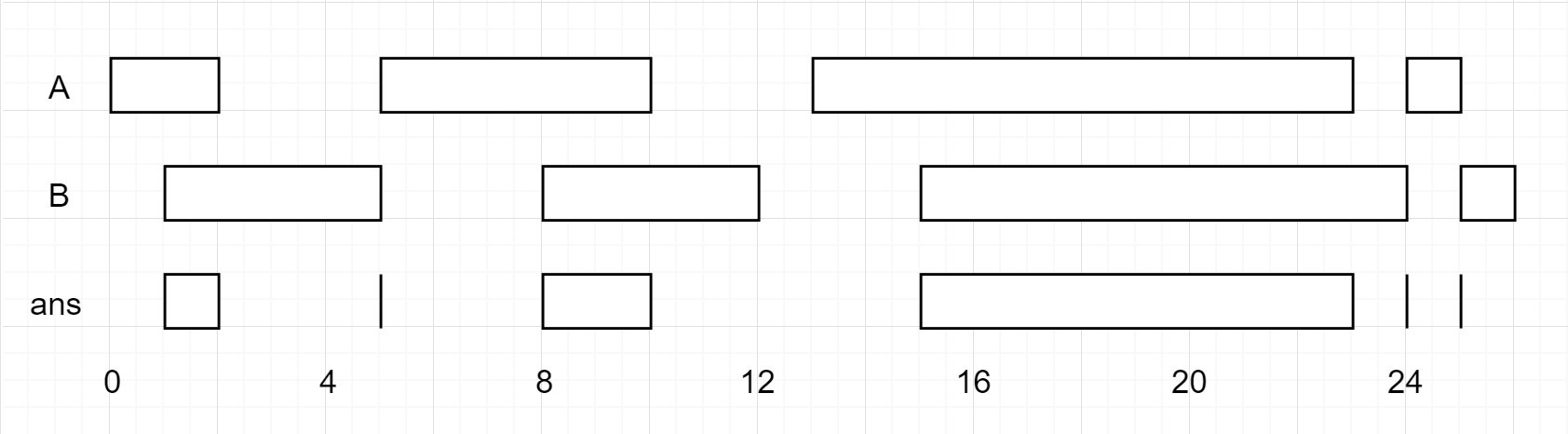
Input: A = [[0,2],[5,10],[13,23],[24,25]], B = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]
Reminder: The inputs and the desired output are lists of Interval objects, and not arrays or lists.

Note:

1. 0 <= A.length < 1000
2. 0 <= B.length < 1000
3. 0 <= A[i].start, A[i].end, B[i].start, B[i].end < 10^9

https://leetcode.com/articles/interval-list-intersections/
https://leetcode.com/problems/interval-list-intersections/discuss/231122/Java-two-pointer-O(m-%2B-n)

In an interval [a, b], call b the "endpoint".

Among the given intervals, consider the interval A[0] with the smallest endpoint. (Without loss of generality, this interval occurs in array A.)

Then, among the intervals in array B, A[0] can only intersect one such interval in array B. (If two intervals in B intersect A[0], then they both share the endpoint of A[0] -- but intervals in B are disjoint, which is a contradiction.)

Algorithm

If A[0] has the smallest endpoint, it can only intersect B[0]. After, we can discard A[0] since it cannot intersect anything else.

Similarly, if B[0] has the smallest endpoint, it can only intersect A[0], and we can discard B[0] after since it cannot intersect anything else.

We use two pointers, i and j, to virtually manage "discarding" A[0] or B[0] repeatedly.

  public Interval[] intervalIntersection(Interval[] A, Interval[] B) {

    List<Interval> ans = new ArrayList<>();

    int i = 0, j = 0;

    while (i < A.length && j < B.length) {

      // Let's check if A[i] intersects B[j].

      // lo - the startpoint of the intersection

      // hi - the endpoint of the intersection

      int lo = Math.max(A[i].start, B[j].start);

      int hi = Math.min(A[i].end, B[j].end);

      if (lo <= hi)

        ans.add(new Interval(lo, hi));

      // Remove the interval with the smallest endpoint

      if (A[i].end < B[j].end)

        i++;

      else

        j++;

    }

    return ans.toArray(new Interval[ans.size()]);

  }

X.
https://leetcode.com/problems/interval-list-intersections/discuss/231108/C%2B%2B-O(n)-%22merge-sort%22

public Interval[] intervalIntersection(Interval[] A, Interval[] B) {
    List<Interval> list = new ArrayList<>();
    for(int i=0, j=0; i < A.length && j < B.length; ) {
        if(A[i].end < B[j].start) i++;
        else if(B[j].end < A[i].start) j++;
        else {
            int start = Math.max(A[i].start, B[j].start);
            int end = Math.min(A[i].end, B[j].end);
            list.add(new Interval(start, end));
            
            if(A[i].end < B[j].end) i++;
            else j++;
        }
    }
    return list.toArray(new Interval[list.size()]);
}