Massive Algorithms: LeetCode 979 - Distribute Coins in Binary Tree

LeetCode 979 - Distribute Coins in Binary Tree

https://leetcode.com/problems/distribute-coins-in-binary-tree/

Given the root of a binary tree with N nodes, each node in the tree has node.val coins, and there are N coins total.

In one move, we may choose two adjacent nodes and move one coin from one node to another. (The move may be from parent to child, or from child to parent.)

Return the number of moves required to make every node have exactly one coin.

Example 1:

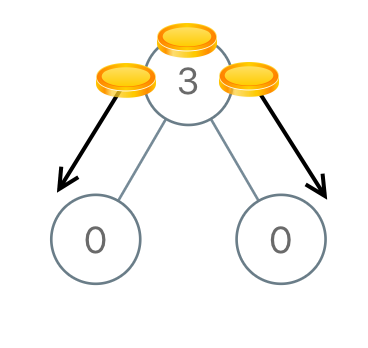
Input: [3,0,0]
Output: 2
Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.

Example 2:

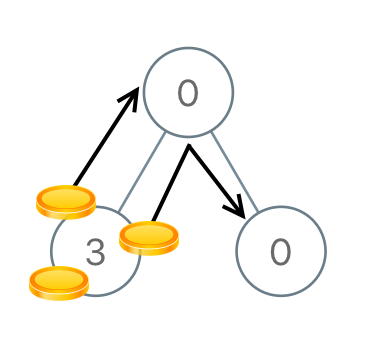
Input: [0,3,0]
Output: 3
Explanation: From the left child of the root, we move two coins to the root [taking two moves].  Then, we move one coin from the root of the tree to the right child.

Example 3:

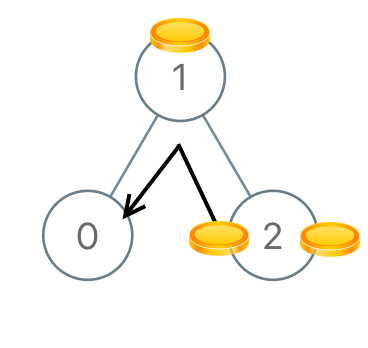
Input: [1,0,2]
Output: 2

Example 4:

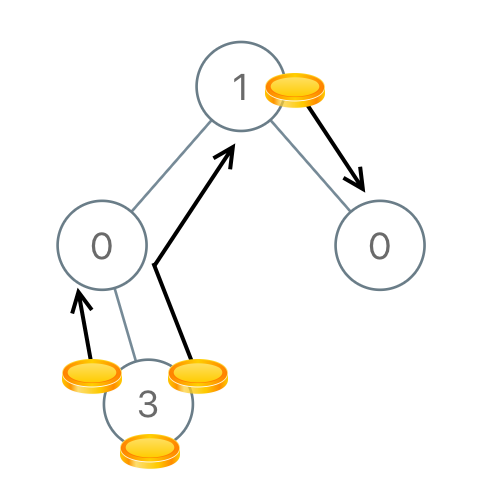
Input: [1,0,0,null,3]
Output: 4

Note:

1<= N <= 100
0 <= node.val <= N

https://leetcode.com/problems/distribute-coins-in-binary-tree/discuss/221939/C%2B%2B-with-picture-post-order-traversal

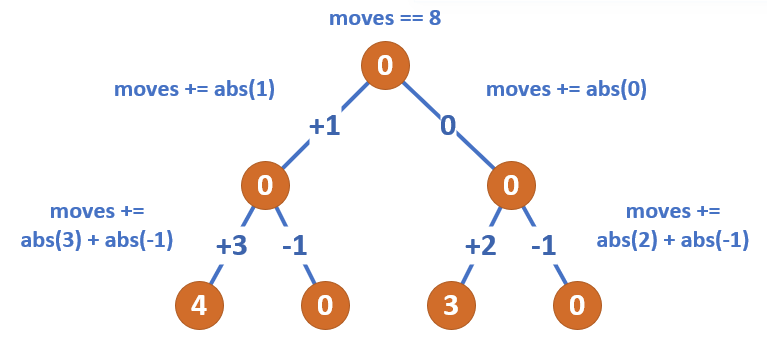
We traverse childs first (post-order traversal), and return the ballance of coins. For example, if we get '+3' from the left child, that means that the left subtree has 3 extra coins to move out. If we get '-1' from the right child, we need to move 1 coin in. So, we increase the number of moves by 4 (3 moves out left + 1 moves in right). We then return the final ballance: -3 (left) + 1 (right) - 1 (keep one coin for the root) + r->val (coins in the root).

int traverse(TreeNode* r, int &moves) {
  if (r == nullptr) return 0;
  int left = traverse(r->left, moves), right = traverse(r->right, moves);
  moves += abs(left) + abs(right);
  return r->val + left + right - 1;
}
int distributeCoins(TreeNode* r, int moves = 0) {
  traverse(r, moves);
  return moves;
}

https://leetcode.com/problems/distribute-coins-in-binary-tree/discuss/221930/JavaC%2B%2BPython-Recursive-Solution

Quite similar problem as this one 968.Binary Tree Cameras.
So I put this as the first solution.
Write a dfs helper, return the number of coins given to the parent.

As somebody may not like global variable,
here is the recursive version without helper.

If we can modify values of tree nodes, we can store the balance in nodes, and use the return value to accumulate the number of moves. This way we can get rid of the helper method.

思路：从叶子到跟寻找，对于每个节点，只能剩下一个。多了的值肯定要全给父亲，少的值全问父亲要，统计一下就好了。

    public int distributeCoins(TreeNode root) {
        int res = 0;
        if (root.left != null) {
            res += distributeCoins(root.left);
            root.val += root.left.val - 1;
            res += Math.abs(root.left.val - 1);
        }
        if (root.right != null) {
            res += distributeCoins(root.right);
            root.val += root.right.val - 1;
            res += Math.abs(root.right.val - 1);
        }
        return res;
    }

private int result;

public int distributeCoins(TreeNode root) {

helper(root);

return result;

}

public int helper(TreeNode root) {

if (root == null)

return 0;

int left = helper(root.left);

int right = helper(root.right);

root.val += left + right;

result += root.val - 1;

return root.val - 1;

}

https://leetcode.com/problems/distribute-coins-in-binary-tree/discuss/222026/Java-Post-order-Traversal-with-Explanation

Helper function returns the amount of coins each node need or have excessively. For each node, it will try to balance the amount of the coins used by its left child and right child.

And it will return a positive number if there is excessive coins which could be used by its parent node, or a negative number if current node or its children need coins.

Each coin (excessive or needed) need one step to be sent to the parent node.

private int steps = 0; 

public int distributeCoins(TreeNode root) {
    postorder(root);
    return steps;
}

// return coins of this level
private int postorder(TreeNode node) {
    if(node == null) return 0;
    
    // coin from children -- post-order traversal
    int coin = postorder(node.left) + postorder(node.right);
 
    // current node coin
    if(node.val == 0) coin += -1; // current node need one coin
    else coin += node.val - 1; // keep one coin for current node
    
    steps += Math.abs(coin); // each coin move up to parent node need 1 step
    return coin; 
}

https://leetcode.com/articles/distribute-coins-in-binary-tree/

If the leaf of a tree has 0 coins (an excess of -1 from what it needs), then we should push a coin from its parent onto the leaf. If it has say, 4 coins (an excess of 3), then we should push 3 coins off the leaf. In total, the number of moves from that leaf to or from its parent is excess = Math.abs(num_coins - 1). Afterwards, we never have to consider this leaf again in the rest of our calculation.

Algorithm

We can use the above fact to build our answer. Let dfs(node) be the excess number of coins in the subtree at or below this node: namely, the number of coins in the subtree, minus the number of nodes in the subtree. Then, the number of moves we make from this node to and from its children is abs(dfs(node.left)) + abs(dfs(node.right)). After, we have an excess of node.val + dfs(node.left) + dfs(node.right) - 1 coins at this node

Time Complexity: $O(N)$ , where $N$ is the number of nodes in the tree.
Space Complexity: $O(H)$ , where $H$ is the height of the tree.

int ans;

public int distributeCoins(TreeNode root) {

ans = 0;

dfs(root);

return ans;

}

public int dfs(TreeNode node) {

if (node == null)

return 0;

int L = dfs(node.left);

int R = dfs(node.right);

ans += Math.abs(L) + Math.abs(R);

return node.val + L + R - 1;

}

https://zhanghuimeng.github.io/post/leetcode-979-distribute-coins-in-binary-tree/

先DFS，到达最底层之后判断每个叶结点上的硬币数量node->val是否恰好为1，如果大于1则把多出来的硬币向父结点移动，总移动数量+=node->val-1，如果小于1则把少的硬币向父结点移动，也就是移动-(1-node->val)枚硬币，总移动数量+=1-node->val。对于其他的结点，因为它们的子结点都已经递归处理完了，所以有多出来的硬币的时候，只能向上移动若干枚硬币或者负的若干枚硬币，也就是和叶结点差不多。

这里面比较好的是移动负数枚硬币这个想法，否则可能还得做第二次递归。

    int ans;
    
    int dfs(TreeNode* root) {
        if (root == NULL) return 0;
        int x = dfs(root->left) + dfs(root->right);
        x += root->val;
        ans += abs(x - 1);
        root->val = 1;
        return x - 1;
    }
    
public:
    int distributeCoins(TreeNode* root) {
        ans = 0;
        dfs(root);
        return ans;
    }

https://www.acwing.com/solution/LeetCode/content/821/
我们自底向上的解决问题，假设每个结点的硬币数量可以为负数。首先我们满足叶子结点，使得叶子结点上的硬币数量都是 1，然后依次向上直到根结点。
通过递归实现这个过程，在当前结点中，首先递归左右儿子，然后如果当前结点的硬币数量不足 1 个，则需要向父亲结点索要 1 - node.val 个；如果当前结点硬币数量大于 1 个，则向父亲结点送出 node.val - 1 个。索要和送出的个数需要累计到答案中。

void solve(TreeNode *rt, TreeNode *parent, int& ans) {
if (rt == nullptr)
return;
solve(rt -> left, rt, ans);
solve(rt -> right, rt, ans);

if (rt -> val < 1) {
parent -> val -= 1 - rt -> val;
ans += 1 - rt -> val;
rt -> val = 1;
}
else if (rt -> val > 1) {
parent -> val += rt -> val - 1;
ans += rt -> val - 1;
rt -> val = 1;
}
}

int distributeCoins(TreeNode* root) {
int ans = 0;
solve(root, nullptr, ans);
return ans;
}
X.

Give the parent node so we can move the coins to the parent directly. int distributeCoins(TreeNode* root, TreeNode* pre = NULL) {

        if (!root) return 0;
        int res = distributeCoins(root->left, root) + distributeCoins(root->right, root);
        if (pre) pre->val += root->val - 1;
        return res + abs(root->val - 1);
    }

https://blog.csdn.net/qq_41156122/article/details/86652292
统计以当前节点为根节点，包括以下（其子孙）共有多少个节点，多少个金币，节点-金币个数的差值的绝对值为不平衡量，需要运进去或运出来，
递归处理，递归的过程中更新答案
int res = 0;
pair<int, int> dfs(TreeNode* root) {

pair<int, int> p;
p.first = 1;
p.second = root->val;
if (root->left != NULL) {
pair<int, int> x = dfs(root->left);
p.first += x.first;
p.second += x.second;
}
if (root->right != NULL) {
pair<int, int> x = dfs(root->right);
p.first += x.first;
p.second += x.second;
}
res += abs(p.first - p.second);
return p;
}
int distributeCoins(TreeNode* root) {
dfs(root);

return res;
}
X. O(N^2)
https://blog.csdn.net/fuxuemingzhu/article/details/86563872
看到二叉树的题目我们一般想到递归，这个题也是如此。这个题是个难的的好题，确实很新颖。

首先，给定了一个二叉树的状态，只要不做重复移动，那么可以证明，移动是无状态的。也就是说，最终的移动次数不会因为先给谁后给谁，或者先移动几个再移动几个，再或者把某些金币移动到近的节点把另外一些金币移动到远的节点而有所不同。总之，我们可以放心大胆地，把金币移动到位，而不需要考虑把具体地金币移动到哪个确切的位置。

所以，我的思路就是分别统计左右子树缺少的金币个数，然后把每个节点和其子树总体的金币分配到位。累计所有节点和其子树所需要的移动次数就是结果。

每个子树缺少的金币数，等于节点数 - 金币数。因为题目确保了所有金币的和等于所有节点数，所以左子树缺少的金币数+该节点缺少的金币数+右子树缺少的金币数=0.我们每次把每个节点和其子树搞平衡，即左子树、该节点、右子树的节点数都等于金币数。注意此时，虽然左右子树总的不缺金币，但是内部仍然分配不均。所以，记录把这个节点搞平衡需要移动的金币数，然后累加上左子树和右子树搞平衡需要移动的金币数即为所求。

下面考虑，如果知道了左右子树需要的金币数，将他们搞平衡需要多少移动步数？答案是左右子树需要的金币数的绝对种子和。这个怎么理解？其实就是需要把子树多的金币挪给根节点，然后再从根节点分配给另一个缺少金币的子树对应的金币。举个栗子：

对于上面的树，左子树缺少-2个金币，右子树缺少1个金币。所以先把左子树多的那两个金币移动到根节点，然后根节点再给右子树分配缺的1个金币即可。因此总的移动次数是左右子树缺少的金币的和。

具体到代码，我们需要一个统计某个子树需要多少金币的函数need()；需要计算把自身，左右子树都平衡，需要移动的coins个数的函数helper()。
int distributeCoins(TreeNode* root) {
int res = 0;
helper(root, res);
return res;
}
// 统计把自身，左右子树都平衡，需要移动的coins个数
void helper(TreeNode* root, int& res) {
if (!root) return;
// 左、右子树缺多少
int left = need(root->left);
int right = need(root->right);
//左，右子树和自身都平衡需要的移动数
res += abs(left) + abs(right);
helper(root->left, res);
helper(root->right, res);
}
// 为了使该子树均匀，需要的coins数
// 节点数 - coins
int need(TreeNode* root) {
if (!root) return 0;
if (count_.count(root))
return count_[root];
int res = need(root->left) + 1 - root->val + need(root->right);
count_[root] = res;
return res;
}
private:
unordered_map<TreeNode*, int> count_;

LeetCode 979 - Distribute Coins in Binary Tree

Labels

Popular Posts