Massive Algorithms: LeetCode 505

LeetCode 505 - The Maze II

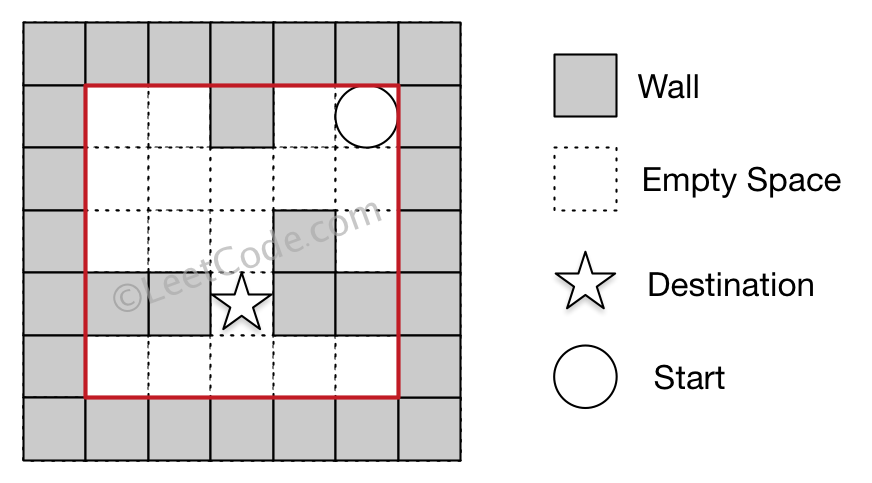
There is a ball in a maze with empty spaces and walls. The ball can go through empty spaces by rolling up, down, left or right, but it won't stop rolling until hitting a wall. When the ball stops, it could choose the next direction.

Given the ball's start position, the destination and the maze, find the shortest distance for the ball to stop at the destination. The distance is defined by the number of empty spaces traveled by the ball from the start position (excluded) to the destination (included). If the ball cannot stop at the destination, return -1.

The maze is represented by a binary 2D array. 1 means the wall and 0 means the empty space. You may assume that the borders of the maze are all walls. The start and destination coordinates are represented by row and column indexes.

Example 1:

Input 1: a maze represented by a 2D array

0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0

Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (4, 4)

Output: 12

Explanation: One shortest way is : left -> down -> left -> down -> right -> down -> right.
             The total distance is 1 + 1 + 3 + 1 + 2 + 2 + 2 = 12.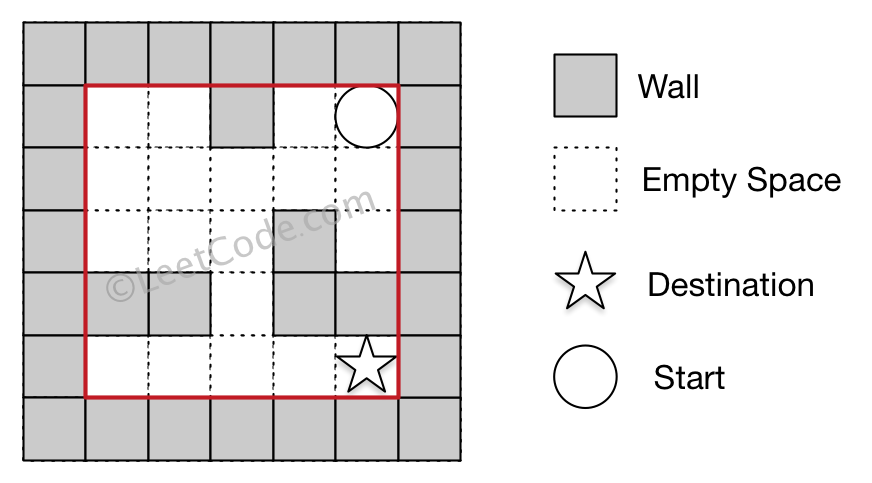

Example 2:

Input 1: a maze represented by a 2D array

0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0

Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (3, 2)

Output: -1

Explanation: There is no way for the ball to stop at the destination.

Note:

There is only one ball and one destination in the maze.
Both the ball and the destination exist on an empty space, and they will not be at the same position initially.
The given maze does not contain border (like the red rectangle in the example pictures), but you could assume the border of the maze are all walls.
The maze contains at least 2 empty spaces, and both the width and height of the maze won't exceed 100.

http://www.cnblogs.com/grandyang/p/6725380.html

我们还可以使用迪杰克斯特拉算法Dijkstra Algorithm来做，LeetCode中能使用到此类高级算法的时候并不多，Network Delay Time 就是一次。该算法是主要是在有向权重图中计算单源最短路径，即单个点到任意点到最短路径。因为这里起点只有一个，所以适用，然后迷宫中的每个格子都可以看作是图中的一个结点，权重可以都看成是1，那么就可以当作是有向权重图来处理。Dijkstra算法的核心是松弛操作Relaxtion，当有对边 (u, v) 是结点u到结点v，如果 dist(v) > dist(u) + w(u, v)，那么 dist(v) 就可以被更新，这是所有这些的算法的核心操作。Dijkstra算法是以起点为中心，向外层层扩展，直到扩展到终点为止。根据这特性，用BFS来实现时再好不过了。为了加快运算速度，我们使用一个优先队列（最小堆）来代替普通的queue，这样我们就能尽量先更新离起点近的位置的dp值，优先队列里同时也存了该点到起点的距离，这个距离不一定是最短距离，可能还能松弛。但是如果其dp值已经小于优先队列中保存的距离，那么就不必更新其周围位置的距离了，因为优先队列中保存的这个距离值不是最短的，使用它来更新周围的dp值没有意义。这相当于利用了松弛操作来进行剪枝，大大提高了运算效率，之后就是类似于之前的BFS的操作了，遍历其周围的四个位置，尝试去更新其dp值。最后还是跟之前一样，如果遍历到了终点，就不要再排入队列了，因为已经得到需要的结果.

X. Approach #4 Using Dijkstra Algorithm and Priority Queue[Accepted]

Time complexity :

O\big(mn*log(mn)\big)

. Complete traversal of maze will be done in the worst case giving a factor of

mn

. Further, poll method is a combination of heapifying(

O\big(log(n)\big)

) and removing the top element(

O(1)

) from the priority queue, and it takes

O(n)

time for

n

elements. In the current case, poll introduces a factor of

log(mn)

public int shortestDistance(int[][] maze, int[] start, int[] dest) {

int[][] distance = new int[maze.length][maze[0].length];

for (int[] row : distance)

Arrays.fill(row, Integer.MAX_VALUE);

distance[start[0]][start[1]] = 0;

dijkstra(maze, start, distance);

return distance[dest[0]][dest[1]] == Integer.MAX_VALUE ? -1 : distance[dest[0]][dest[1]];

}

public void dijkstra(int[][] maze, int[] start, int[][] distance) {

int[][] dirs = { { 0, 1 }, { 0, -1 }, { -1, 0 }, { 1, 0 } };

PriorityQueue<int[]> queue = new PriorityQueue<>((a, b) -> a[2] - b[2]);

queue.offer(new int[] { start[0], start[1], 0 });

while (!queue.isEmpty()) {

int[] s = queue.poll();

if (distance[s[0]][s[1]] < s[2])

continue;

for (int[] dir : dirs) {

int x = s[0] + dir[0];

int y = s[1] + dir[1];

int count = 0;

while (x >= 0 && y >= 0 && x < maze.length && y < maze[0].length && maze[x][y] == 0) {

x += dir[0];

y += dir[1];

count++;

}

if (distance[s[0]][s[1]] + count < distance[x - dir[0]][y - dir[1]]) {

distance[x - dir[0]][y - dir[1]] = distance[s[0]][s[1]] + count;

queue.offer(new int[] { x - dir[0], y - dir[1], distance[x - dir[0]][y - dir[1]] });

}

We need to use PriorityQueue instead of standard queue, and record the minimal length of each point.

Why using PriorityQueue?

We can consider this question as a shortest-route graph problem, that is, each stoppable point is a vertical, where every possible path between two nodes is an edge.
In this way, we can using Dijkstra algorithm to solve this problem, and that's why we use PriorityQueue.

public class Position implements Comparable<Position> { int distance; int x; int y; public Position(int x, int y, int d) { this.x=x; this.y=y; this.distance=d; } public int compareTo(Position o) { return this.distance-o.distance; } } public int shortestDistance(int[][] maze, int[] start, int[] destination) { for(int i=0;i<maze.length;i++) for(int j=0;j<maze[0].length;j++) maze[i][j]=maze[i][j]==0 ? Integer.MAX_VALUE :-1; return bfs(maze,start,destination); } public int bfs(int[][] maze, int [] start, int [] destination) { int[][] dirs = new int[][]{{-1,0},{1,0},{0,-1},{0,1}}; PriorityQueue<Position> queue = new PriorityQueue<>(); Position startPos = new Position(start[0],start[1],0); maze[start[0]][start[1]]=0; queue.offer(startPos); while(!queue.isEmpty()) { Position cur = queue.poll(); for(int[] dir : dirs) { int distance=0; int x = cur.x+dir[0]; int y=cur.y+dir[1]; while(x>=0 && x<maze.length && y>=0 && y<maze[0].length && maze[x][y]!=-1) { x+=dir[0]; y+=dir[1]; distance++; } x-=dir[0]; y-=dir[1]; if(maze[x][y]<=cur.distance+distance) continue; maze[x][y]=cur.distance+distance; if(x==destination[0] && y==destination[1]) return maze[x][y]; queue.offer(new Position(x,y,cur.distance+distance)); } } return -1; }
https://segmentfault.com/a/1190000008323436
Is this right?
这道题要求最短的路径，普通的遍历dfs和bfs都是可以做的，但是求最短路径的话还是用Dijksra。这里相当于每个点有至多4条edge相连，每条edge的weight就是到墙之前的长度。

    public int shortestDistance(int[][] maze, int[] start, int[] destination) {
        // base case
        if(Arrays.equals(start, destination)) return 0;
        
        m = maze.length; n = maze[0].length;
        
        return shortestPath(maze, start, destination);
    }
    int m, n;
    int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
    
    private int shortestPath(int[][] maze, int[] start, int[] destination) {
        // get the vertice has the minimum distance to start
        PriorityQueue<Node> minHeap = new PriorityQueue<>((a, b) -> a.distance - b.distance);
        minHeap.offer(new Node(start[0], start[1], 0));
        
        // map that contains information of node: distance to start point
        int[][] visited = new int[m][n];
        for(int[] arr : visited) Arrays.fill(arr, Integer.MAX_VALUE);
        
        while(!minHeap.isEmpty()) {
            Node cur = minHeap.poll();
            // find the shortest path
            if(cur.x == destination[0] && cur.y == destination[1]) return cur.distance;
            
            for(int[] dir : dirs) {
                int nx = cur.x, ny = cur.y;
                while(isInMaze(nx + dir[0], ny + dir[1]) && maze[nx + dir[0]][ny + dir[1]] != 1) {
                    nx += dir[0];  ny += dir[1];
                }
                int distance = cur.distance + Math.abs(nx - cur.x) + Math.abs(ny - cur.y);
                if(visited[nx][ny] > distance) {
                    minHeap.offer(new Node(nx, ny, distance));
                    visited[nx][ny] = distance;
                }
            }
        }
        return -1;
    }
    
    private boolean isInMaze(int x, int y) {
        return x >= 0 && x < m && y >= 0 && y < n;
    }
    
    class Node {
        int x;
        int y;
        // distance to start point
        int distance;
        Node(int x, int y, int distance) {
            this.x = x;
            this.y = y;
            this.distance = distance;
        }
    }

https://discuss.leetcode.com/topic/77472/similar-to-the-maze-easy-understanding-java-bfs-solution

Why using PriorityQueue?

We have to traverse all approaches

    class Point {
        int x,y,l;
        public Point(int _x, int _y, int _l) {x=_x;y=_y;l=_l;}
    }
    public int shortestDistance(int[][] maze, int[] start, int[] destination) {
        int m=maze.length, n=maze[0].length;
        int[][] length=new int[m][n]; // record length
        for (int i=0;i<m*n;i++) length[i/n][i%n]=Integer.MAX_VALUE;
        int[][] dir=new int[][] {{-1,0},{0,1},{1,0},{0,-1}};
        PriorityQueue<Point> list=new PriorityQueue<>((o1,o2)->o1.l-o2.l); // using priority queue
        list.offer(new Point(start[0], start[1], 0));
        while (!list.isEmpty()) {
            Point p=list.poll();
            if (length[p.x][p.y]<=p.l) continue; // if we have already found a route shorter
            length[p.x][p.y]=p.l;
            for (int i=0;i<4;i++) {
                int xx=p.x, yy=p.y, l=p.l;
                while (xx>=0 && xx<m && yy>=0 && yy<n && maze[xx][yy]==0) {
                    xx+=dir[i][0];
                    yy+=dir[i][1];
                    l++;
                }
                xx-=dir[i][0];
                yy-=dir[i][1];
                l--;
                list.offer(new Point(xx, yy, l));
            }
        }
        return length[destination[0]][destination[1]]==Integer.MAX_VALUE?-1:length[destination[0]][destination[1]];
    }

X. DFS
https://discuss.leetcode.com/topic/78924/java-accepted-dfs

static final int[] DIRS = {0, 1, 0, -1, 0};
public int shortestDistance(int[][] maze, int[] start, int[] destination) {
    int[][] dist = new int[maze.length][maze[0].length];
    dist[start[0]][start[1]] = 1;
    dfs(start[0], start[1], destination, maze, dist);
    return dist[destination[0]][destination[1]] - 1;
}
void dfs(int row, int col, int[] dest, int[][] maze, int[][] dist) {
    if (row == dest[0] && col == dest[1]) return;
    int m = maze.length, n = maze[0].length;
    for (int d = 0; d < 4; ++d) {
        int i = row, j = col, p = DIRS[d], q = DIRS[d + 1], len = dist[row][col];
        while (i + p >= 0 && i + p < m && j + q >= 0 && j + q < n && maze[i + p][j + q] == 0) {
            i += p;
            j += q;
            len++;
        }
        if (dist[i][j] > 0 && len >= dist[i][j]) continue;
        dist[i][j] = len;
        dfs(i, j, dest, maze, dist);
    }
}

http://bookshadow.com/weblog/2017/01/29/leetcode-the-maze-ii/

https://leetcode.com/articles/the-maze-ii/
X. DFS

Time complexity : $O(m*n*\text{max}(m,n))$ . Complete traversal of maze will be done in the worst case. Here, $m$ and $n$ refers to the number of rows and columns of the maze. Further, for every current node chosen, we can travel upto a maximum depth of $\text{max}(m,n)$ in any direction.
Space complexity : $O(mn)$ . $distance$ array of size $m*n$ is used.

    public int shortestDistance(int[][] maze, int[] start, int[] dest) {
        int[][] distance = new int[maze.length][maze[0].length];
        for (int[] row: distance)
            Arrays.fill(row, Integer.MAX_VALUE);
        distance[start[0]][start[1]] = 0;
        dfs(maze, start, distance);
        return distance[dest[0]][dest[1]] == Integer.MAX_VALUE ? -1 : distance[dest[0]][dest[1]];
    }

    public void dfs(int[][] maze, int[] start, int[][] distance) {
        int[][] dirs={{0,1}, {0,-1}, {-1,0}, {1,0}};
        for (int[] dir: dirs) {
            int x = start[0] + dir[0];
            int y = start[1] + dir[1];
            int count = 0;
            while (x >= 0 && y >= 0 && x < maze.length && y < maze[0].length && maze[x][y] == 0) {
                x += dir[0];
                y += dir[1];
                count++;
            }
            if (distance[start[0]][start[1]] + count < distance[x - dir[0]][y - dir[1]]) {
                distance[x - dir[0]][y - dir[1]] = distance[start[0]][start[1]] + count;
                dfs(maze, new int[]{x - dir[0],y - dir[1]}, distance);
            }
        }
    }

X. BFS

    public int shortestDistance(int[][] maze, int[] start, int[] dest) {
        int[][] distance = new int[maze.length][maze[0].length];
        for (int[] row: distance)
            Arrays.fill(row, Integer.MAX_VALUE);
        distance[start[0]][start[1]] = 0;
         int[][] dirs={{0, 1} ,{0, -1}, {-1, 0}, {1, 0}};
        Queue < int[] > queue = new LinkedList < > ();
        queue.add(start);
        while (!queue.isEmpty()) {
            int[] s = queue.remove();
            for (int[] dir: dirs) {
                int x = s[0] + dir[0];
                int y = s[1] + dir[1];
                int count = 0;
                while (x >= 0 && y >= 0 && x < maze.length && y < maze[0].length && maze[x][y] == 0) {
                    x += dir[0];
                    y += dir[1];
                    count++;
                }
                if (distance[s[0]][s[1]] + count < distance[x - dir[0]][y - dir[1]]) {
                    distance[x - dir[0]][y - dir[1]] = distance[s[0]][s[1]] + count;
                    queue.add(new int[] {x - dir[0], y - dir[1]});
                }
            }
        }
        return distance[dest[0]][dest[1]] == Integer.MAX_VALUE ? -1 : distance[dest[0]][dest[1]];
    }

The criteria used for heapifying is that the node which is unvisited and at the smallest distance from the

start

node, is always present on the top of the heap. Thus, the node to be chosen as the current node, is always present at the front of the

queue

Time complexity :

O\big(mn*log(mn)\big)

. Complete traversal of maze will be done in the worst case giving a factor of

mn

. Further, poll method is a combination of heapifying(

O\big(log(n)\big)

) and removing the top element(

O(1)

) from the priority queue, and it takes

O(n)

time for

n

elements. In the current case, poll introduces a factor of

log(mn)

    public int shortestDistance(int[][] maze, int[] start, int[] dest) {
        int[][] distance = new int[maze.length][maze[0].length];
        for (int[] row: distance)
            Arrays.fill(row, Integer.MAX_VALUE);
        distance[start[0]][start[1]] = 0;
        dijkstra(maze, start, distance);
        return distance[dest[0]][dest[1]] == Integer.MAX_VALUE ? -1 : distance[dest[0]][dest[1]];
    }

    public void dijkstra(int[][] maze, int[] start, int[][] distance) {
        int[][] dirs={{0,1},{0,-1},{-1,0},{1,0}};
        PriorityQueue < int[] > queue = new PriorityQueue < > ((a, b) -> a[2] - b[2]);
        queue.offer(new int[]{start[0],start[1],0});
        while (!queue.isEmpty()) {
            int[] s = queue.poll();
            if(distance[s[0]][s[1]] < s[2])
                continue;
            for (int[] dir: dirs) {
                int x = s[0] + dir[0];
                int y = s[1] + dir[1];
                int count = 0;
                while (x >= 0 && y >= 0 && x < maze.length && y < maze[0].length && maze[x][y] == 0) {
                    x += dir[0];
                    y += dir[1];
                    count++;
                }
                if (distance[s[0]][s[1]] + count < distance[x - dir[0]][y - dir[1]]) {
                    distance[x - dir[0]][y - dir[1]] = distance[s[0]][s[1]] + count;
                    queue.offer(new int[]{x - dir[0], y - dir[1], distance[x - dir[0]][y - dir[1]]});
                }
            }
        }
    }

X. Using Dijkstra Algorithm

Dijkstra's Algorithm is a very famous graph algorithm, which is used to find the shortest path from any

start

node to any

destination

node in the given weighted graph(the edges of the graph represent the distance between the nodes).

The algorithm consists of the following steps:

Assign a tentative distance value to every node: set it to zero for our $start$ node and to infinity for all other nodes.
Set the $start$ node as $current$ node. Mark it as visited.
For the $current$ node, consider all of its neighbors and calculate their tentative distances. Compare the newly calculated tentative distance to the current assigned value and assign the smaller one to all the neighbors. For example, if the current node A is marked with a distance of 6, and the edge connecting it with a neighbor B has length 2, then the distance to B (through A) will be 6 + 2 = 8. If B was previously marked with a distance greater than 8 then change it to 8. Otherwise, keep the current value.
When we are done considering all of the neighbors of the current node, mark the $current$ node as visited. A visited node will never be checked again.
If the $destination$ node has been marked visited or if the smallest tentative distance among all the nodes left is infinity(indicating that the $destination$ can't be reached), then stop. The algorithm has finished.
Otherwise, select the unvisited node that is marked with the smallest tentative distance, set it as the new $current$ node, and go back to step 3.

Time complexity :

O((mn)^2)

. Complete traversal of maze will be done in the worst case and function minDistance takes

O(mn)

time.

    public int shortestDistance(int[][] maze, int[] start, int[] dest) {
        int[][] distance = new int[maze.length][maze[0].length];
        boolean[][] visited = new boolean[maze.length][maze[0].length];
        for (int[] row: distance)
            Arrays.fill(row, Integer.MAX_VALUE);
        distance[start[0]][start[1]] = 0;
        dijkstra(maze, distance, visited);
        return distance[dest[0]][dest[1]] == Integer.MAX_VALUE ? -1 : distance[dest[0]][dest[1]];
    }
    public int[] minDistance(int[][] distance, boolean[][] visited) {
        int[] min={-1,-1};
        int min_val = Integer.MAX_VALUE;
        for (int i = 0; i < distance.length; i++) {
            for (int j = 0; j < distance[0].length; j++) {
                if (!visited[i][j] && distance[i][j] < min_val) {
                    min = new int[] {i, j};
                    min_val = distance[i][j];
                }
            }
        }
        return min;
    }
    public void dijkstra(int[][] maze, int[][] distance, boolean[][] visited) {
        int[][] dirs={{0,1},{0,-1},{-1,0},{1,0}};
        while (true) {
            int[] s = minDistance(distance, visited);
            if (s[0] < 0)
                break;
            visited[s[0]][s[1]] = true;
            for (int[] dir: dirs) {
                int x = s[0] + dir[0];
                int y = s[1] + dir[1];
                int count = 0;
                while (x >= 0 && y >= 0 && x < maze.length && y < maze[0].length && maze[x][y] == 0) {
                    x += dir[0];
                    y += dir[1];
                    count++;
                }
                if (distance[s[0]][s[1]] + count < distance[x - dir[0]][y - dir[1]]) {
                    distance[x - dir[0]][y - dir[1]] = distance[s[0]][s[1]] + count;
                }
            }
        }
    }

LeetCode 505 - The Maze II

Labels

Popular Posts