Leetcode 490, 505 - The Maze I,III
http://bookshadow.com/weblog/2017/01/29/leetcode-the-maze-ii/
X. BFS
https://discuss.leetcode.com/topic/77361/short-clean-and-straight-forward-bfs-solution-with-priorityqueue
https://discuss.leetcode.com/topic/77474/similar-to-the-maze-ii-easy-understanding-java-bfs-solution
https://discuss.leetcode.com/topic/77123/java-bfs-solution-with-queue-standard-bfs-15ms-beats-85-71
https://discuss.leetcode.com/topic/77074/clear-java-accepted-dfs-solution-with-explanation
http://144.168.59.81:8081/2017/02/01/leetcode_499/
X. DFS
https://blog.csdn.net/magicbean2/article/details/78727575
也就是在搜索的过程中维护一个截止当前的最优解(需要包含路径字符串已经路径长度)。在当前的位置上沿着当前方向一直前进,直到遇到障碍。如果在前进的过程中遇到了洞,那么就更新结果。否则当走到尽头的时候就改变方向(只能右转或者左转,不可继续或者逆向返回)。我们在深度优先搜索的过程中,保持down->left->right->up这样一个方向,可以保证字典序最小的结果最小被获得。
https://www.codetd.com/article/3730430
https://discuss.leetcode.com/topic/77074/clear-java-accepted-dfs-solution-with-explanation/3
http://bookshadow.com/weblog/2017/01/29/leetcode-the-maze-ii/
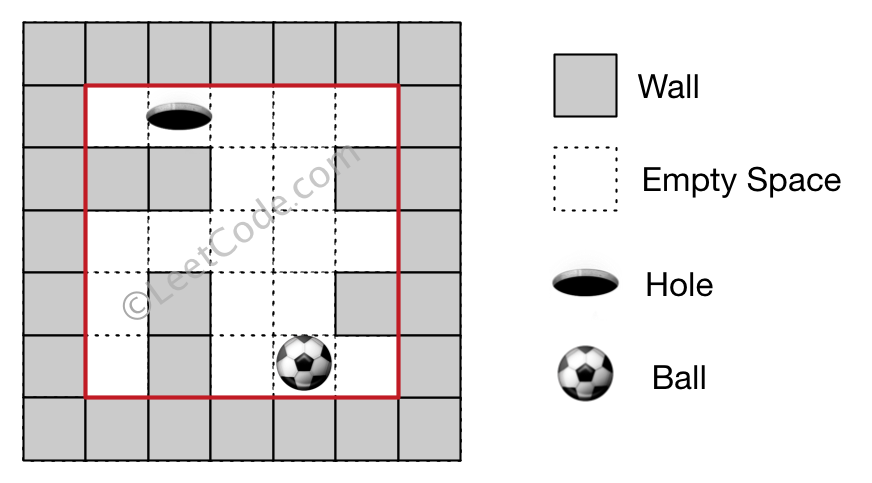
There is a ball in a maze with empty spaces and walls. The ball can go through empty spaces by rolling up (u), down (d), left (l) or right (r), but it won't stop rolling until hitting a wall. When the ball stops, it could choose the next direction. There is also a hole in this maze. The ball will drop into the hole if it rolls on to the hole.
Given the ball position, the hole position and the maze, your job is to find out how the ball could drop into the hole by moving shortest distance in the maze. The distance is defined by the number of empty spaces the ball go through from the start position (exclude) to the hole (include). Output the moving directions by using 'u', 'd', 'l' and 'r'. Since there may have several different shortest ways, you should output the lexicographically smallest way. If the ball cannot reach the hole, output "impossible".
The maze is represented by a binary 2D array. 1 means the wall and 0 means the empty space. You may assume that the borders of the maze are all walls. The ball and hole coordinates are represented by row and column indexes.
Example 1
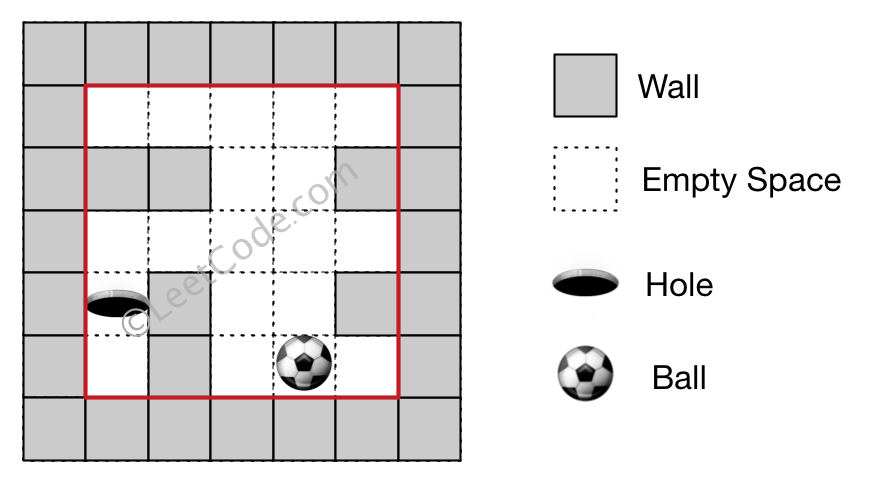
Example 2
Note:
- There are only one ball and one hole in the maze.
- The ball and hole will only exist in the empty space, and they will not at the same position initially.
- The given maze doesn't contain border (like the red rectangle in the example pictures), but you should assume the border of the maze are all walls.
- The maze contains at least 2 empty spaces, and the length and width of the maze won't exceed 30.
https://github.com/Turingfly/leetcode/blob/master/LeetCode/src/bfs/_499_TheMazeIII.java
http://www.cnbolgs.com/grandyang/p/6746528.html这道题在之前的两道The Maze II和The Maze的基础上又做了些改变,在路径中间放了个陷阱,让球在最小步数内滚到陷阱之中,此时返回的并不是最小步数,而是滚动的方向,用u, r, d, l 这四个字母来分别表示上右下左,而且在步数相等的情况下,让我们返回按字母排序小的答案。相对于迷宫二那题来说,难度是增加了一些,但我们还是可以借鉴之前那道题的思路,我们还是需要用一个二位数组dists,其中dists[i][j]表示到达(i,j)这个位置时需要的最小步数,我们都初始化为整型最大值,在后在遍历的过程中不断用较小值来更新每个位置的步数值。我们还需要用一个哈希表来建立每个位置跟滚到该位置的方向字符串之间的映射,这里我们用一个trick,将二维坐标转(i,j)为一个数字i*n+j,这实际上就是把二维数组拉成一维数组的操作,matlab中很常见的操作。还有需要注意的是,一滚到底的操作需要稍作修改,之前我们都是一直滚到墙里面或者界外才停止,然后做退一步处理,就是小球能滚到的位置,这里我们滚的时候要判断陷阱,如果滚到了陷阱,那么我们也停下来,注意这时候不需要做后退一步处理。然后我们还是比较当前步数是否小于dists中的原有步数,小于的话就更新dists,然后更新哈希表中的映射方向字符串,然后对于不是陷阱的点,我们加入队列queue中继续滚。另一点跟迷宫二不同的之处在于,这里还要处理另一种情况,就是当最小步数相等的时候,并且新的滚法的方向字符串的字母顺序要小于原有的字符串的时候,我们也需要更新哈希表的映射,并且判断是否需要加入队列queue中
预处理 + 单源最短路
下面的解法采用Dijkstra算法,比上面的解法效率更优http://www.cnbolgs.com/grandyang/p/6746528.html这道题在之前的两道The Maze II和The Maze的基础上又做了些改变,在路径中间放了个陷阱,让球在最小步数内滚到陷阱之中,此时返回的并不是最小步数,而是滚动的方向,用u, r, d, l 这四个字母来分别表示上右下左,而且在步数相等的情况下,让我们返回按字母排序小的答案。相对于迷宫二那题来说,难度是增加了一些,但我们还是可以借鉴之前那道题的思路,我们还是需要用一个二位数组dists,其中dists[i][j]表示到达(i,j)这个位置时需要的最小步数,我们都初始化为整型最大值,在后在遍历的过程中不断用较小值来更新每个位置的步数值。我们还需要用一个哈希表来建立每个位置跟滚到该位置的方向字符串之间的映射,这里我们用一个trick,将二维坐标转(i,j)为一个数字i*n+j,这实际上就是把二维数组拉成一维数组的操作,matlab中很常见的操作。还有需要注意的是,一滚到底的操作需要稍作修改,之前我们都是一直滚到墙里面或者界外才停止,然后做退一步处理,就是小球能滚到的位置,这里我们滚的时候要判断陷阱,如果滚到了陷阱,那么我们也停下来,注意这时候不需要做后退一步处理。然后我们还是比较当前步数是否小于dists中的原有步数,小于的话就更新dists,然后更新哈希表中的映射方向字符串,然后对于不是陷阱的点,我们加入队列queue中继续滚。另一点跟迷宫二不同的之处在于,这里还要处理另一种情况,就是当最小步数相等的时候,并且新的滚法的方向字符串的字母顺序要小于原有的字符串的时候,我们也需要更新哈希表的映射,并且判断是否需要加入队列queue中
预处理 + 单源最短路
X. BFS
https://discuss.leetcode.com/topic/77361/short-clean-and-straight-forward-bfs-solution-with-priorityqueue
The idea is just using BFS with a PriorityQueue(dijkstra's algorithm), PriorityQueue polls out the Coordinate with the minimum distance, if there are two with same distance, we compare their lexicographical order, by this way, we can ensure that we get the lexicographically smallest way in the end.
class Coordinate implements Comparable<Coordinate> {
int x, y, dist;
String moves;
public Coordinate(int x, int y, int dist, String moves) {
this.x = x;
this.y = y;
this.dist = dist;
this.moves = moves;
}
public int compareTo(Coordinate that) {
if (this.dist != that.dist) return this.dist - that.dist;
return this.moves.compareTo(that.moves);
}
}
int[][] dirs = {{1, 0}, {0, -1}, {0, 1}, {-1, 0}};
char[] dirc = {'d', 'l', 'r', 'u'};
public String findShortestWay(int[][] maze, int[] ball, int[] hole) {
int m = maze.length, n = maze[0].length;
boolean[][] visited = new boolean[m][n];
PriorityQueue<Coordinate> pq = new PriorityQueue<>();
pq.add(new Coordinate(ball[0], ball[1], 0, ""));
while(!pq.isEmpty()) {
Coordinate curr = pq.poll();
if (curr.x == hole[0] && curr.y == hole[1]) {
return curr.moves;
}
if (!visited[curr.x][curr.y]) {
visited[curr.x][curr.y] = true;
for (int direction = 0; direction < 4; direction++) {
Coordinate next = moveForward(maze, curr, direction, hole);
pq.add(new Coordinate(next.x, next.y, next.dist, next.moves + dirc[direction]));
}
}
}
return "impossible";
}
/*
Start from current position move forward in one direction until hit the wall, return the last position before hitting the wall
*/
private Coordinate moveForward(int[][] maze, Coordinate curr, int direction, int[] hole) {
int m = maze.length, n = maze[0].length;
int nx = curr.x, ny = curr.y, dis = curr.dist;
while (nx >= 0 && nx < m && ny >= 0 && ny < n && maze[nx][ny] == 0) {
nx += dirs[direction][0];
ny += dirs[direction][1];
dis++;
if (nx == hole[0] && ny == hole[1]) {
return new Coordinate(nx, ny, dis, curr.moves);
}
}
// back up one step from wall
nx -= dirs[direction][0];
ny -= dirs[direction][1];
dis--;
return new Coordinate(nx, ny, dis, curr.moves);
}
We just need to implement
Comparable of Point, and record the route of every point. class Point implements Comparable<Point> {
int x,y,l;
String s;
public Point(int _x, int _y) {x=_x;y=_y;l=Integer.MAX_VALUE;s="";}
public Point(int _x, int _y, int _l,String _s) {x=_x;y=_y;l=_l;s=_s;}
public int compareTo(Point p) {return l==p.l?s.compareTo(p.s):l-p.l;}
}
public String findShortestWay(int[][] maze, int[] ball, int[] hole) {
int m=maze.length, n=maze[0].length;
Point[][] points=new Point[m][n];
for (int i=0;i<m*n;i++) points[i/n][i%n]=new Point(i/n, i%n);
int[][] dir=new int[][] {{-1,0},{0,1},{1,0},{0,-1}};
String[] ds=new String[] {"u","r","d","l"};
PriorityQueue<Point> list=new PriorityQueue<>(); // using priority queue
list.offer(new Point(ball[0], ball[1], 0, ""));
while (!list.isEmpty()) {
Point p=list.poll();
if (points[p.x][p.y].compareTo(p)<=0) continue; // if we have already found a route shorter
points[p.x][p.y]=p;
for (int i=0;i<4;i++) {
int xx=p.x, yy=p.y, l=p.l;
while (xx>=0 && xx<m && yy>=0 && yy<n && maze[xx][yy]==0 && (xx!=hole[0] || yy!=hole[1])) {
xx+=dir[i][0];
yy+=dir[i][1];
l++;
}
if (xx!=hole[0] || yy!=hole[1]) { // check the hole
xx-=dir[i][0];
yy-=dir[i][1];
l--;
}
list.offer(new Point(xx, yy, l, p.s+ds[i]));
}
}
return points[hole[0]][hole[1]].l==Integer.MAX_VALUE?"impossible":points[hole[0]][hole[1]].s;
}https://discuss.leetcode.com/topic/77123/java-bfs-solution-with-queue-standard-bfs-15ms-beats-85-71
public class Element {
int direction;
int row, col;
String moves;
Element(int row, int col, String moves, int direction) {
this.row = row;
this.col = col;
this.moves = moves;
this.direction = direction;
}
}
public String findShortestWay(int[][] maze, int[] ball, int[] hole) {
//initialization
int m = maze.length, n = maze[0].length;
Queue<Element> path = new LinkedList<>();
char[] directions = {'d', 'l', 'r', 'u'};
int[] deltaRow = {1, 0, 0, -1};
int[] deltaCol = {0, -1, 1, 0};
boolean[][][] visited = new boolean[m][n][4];
//add start point
for (int i = 0; i < 4; i++) {
int row = ball[0] + deltaRow[i], col = ball[1] + deltaCol[i];
if (row >= 0 && row < m && col >= 0 && col < n && maze[row][col] == 0) {
path.add(new Element(row, col, String.valueOf(directions[i]), i));
}
}
while (!path.isEmpty()) {
Element top = path.poll();
visited[top.row][top.col][top.direction] = true;
if (top.row == hole[0] && top.col == hole[1]) {
return top.moves;
}
//go with same direction
int nextRow = top.row + deltaRow[top.direction];
int nextCol = top.col + deltaCol[top.direction];
if (nextRow >= 0 && nextRow < m && nextCol >= 0 && nextCol < n && maze[nextRow][nextCol] == 0) {
//no hit wall
if (!visited[nextRow][nextCol][top.direction]) {
path.offer(new Element(nextRow, nextCol, top.moves, top.direction));
}
} else {
//hit the wall, change direction
for (int direction = 0; direction < 4; direction++) {
if (direction != top.direction) {
nextRow = top.row + deltaRow[direction];
nextCol = top.col + deltaCol[direction];
if (nextRow >= 0 && nextRow < m && nextCol >= 0 && nextCol < n && maze[nextRow][nextCol] == 0
&& !visited[nextRow][nextCol][direction]) {
path.offer(new Element(nextRow, nextCol, top.moves + directions[direction], direction));
}
}
}
}
}
return "impossible";
}https://discuss.leetcode.com/topic/77074/clear-java-accepted-dfs-solution-with-explanation
http://144.168.59.81:8081/2017/02/01/leetcode_499/
I really appreciated your
int[][] map and use index of int[][] dirs to represent r,u,l,d, it simplified many works for me. int[][] dirs = {{1, 0}, {0, -1}, {0, 1}, {-1, 0}};
char[] dirc = {'d', 'l', 'r', 'u'};
public String findShortestWay(int[][] maze, int[] ball, int[] hole) {
int m = maze.length, n = maze[0].length;
String minS = null;
int min = Integer.MAX_VALUE;
int[][] map = new int[m][n]; // min distance till this node
for (int i = 0; i < m; i++) Arrays.fill(map[i], Integer.MAX_VALUE);
Node start = new Node(ball[0], ball[1], 0, ""); // start point
PriorityQueue<Node> q = new PriorityQueue();
q.add(start);
boolean[][] vis = new boolean[m][n]; // visited nodes
while (!q.isEmpty()) {
// extract min, get the cur position
Node cur = q.poll();
vis[cur.x][cur.y] = true;
// try 4 dirs
for (int d = 0; d < 4; d++) {
int x = cur.x, y = cur.y;
// start point, or get the end point
while (x + dirs[d][0] < m && x + dirs[d][0] >= 0 && y + dirs[d][1] < n && y + dirs[d][1] >= 0
&& maze[x + dirs[d][0]][y + dirs[d][1]] != 1) {
x += dirs[d][0];
y += dirs[d][1];
if (vis[x][y] || (x == hole[0] && y == hole[1])) break;
}
int step = cur.step + Math.abs(x - cur.x) + Math.abs(y - cur.y);
if (vis[x][y] || step > map[x][y]) continue;
// update distance
map[x][y] = step;
// next node
Node next = new Node(x, y, step, cur.route + dirc[d]);
// System.out.println(next.route); /// this damn line!!! slowed my solution...
// reach the end
if (x == hole[0] && y == hole[1]) {
if (step == min && (minS == null || next.route.compareTo(minS) < 0)) {
minS = next.route;
} else if (step < min) {
min = step;
minS = next.route;
}
// if reach the end in this direction, we don't need to try other directions
break;
}
q.add(next);
}
}
return minS == null ? "impossible" : minS;
}
class Node implements Comparable<Node> {
int x, y, step;
String route; // a string formed by directions along the way
public Node(int x, int y, int step, String route) {
this.x = x;
this.y = y;
this.step = step;
this.route = route;
}
public boolean equals(Node a, Node b) {
return a.x == b.x && a.y == b.y;
}
public int compareTo(Node that) {
return this.step - that.step;
}
}X. DFS
https://blog.csdn.net/magicbean2/article/details/78727575
也就是在搜索的过程中维护一个截止当前的最优解(需要包含路径字符串已经路径长度)。在当前的位置上沿着当前方向一直前进,直到遇到障碍。如果在前进的过程中遇到了洞,那么就更新结果。否则当走到尽头的时候就改变方向(只能右转或者左转,不可继续或者逆向返回)。我们在深度优先搜索的过程中,保持down->left->right->up这样一个方向,可以保证字典序最小的结果最小被获得。
https://www.codetd.com/article/3730430
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
if(maze.length == 0 || maze[0].length == 0) return false;
if(start[0] == destination[0] && start[1] == destination[1]) return true;
m = maze.length; n = maze[0].length;
boolean[][] visited = new boolean[m][n];
return dfs(maze, start, destination, visited);
}
int m, n;
int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
private boolean dfs(int[][] maze, int[] cur, int[] dest, boolean[][] visited) {
// already visited
if(visited[cur[0]][cur[1]]) return false;
// reach destination
if(Arrays.equals(cur, dest)) return true;
visited[cur[0]][cur[1]] = true;
for(int[] dir : dirs) {
int nx = cur[0], ny = cur[1];
while(notWall(nx + dir[0], ny + dir[1]) && maze[nx+dir[0]][ny+dir[1]] != 1) {
nx += dir[0]; ny += dir[1];
}
if(dfs(maze, new int[] {nx, ny}, dest, visited)) return true;
}
return false;
}
private boolean notWall(int x, int y) {
return x >= 0 && x < m && y >= 0 && y < n;
}
int minStep;
int m, n;
String res;
int[][] dirs = {{1, 0}, {0, 1}, {0, -1}, {-1, 0}};
String[] dirc = {"d", "r", "l", "u"}; // 0123
public String findShortestWay(int[][] maze, int[] ball, int[] hole) {
this.m = maze.length;
this.n = maze[0].length;
this.minStep = Integer.MAX_VALUE;
this.res = null;
boolean[][] vis = new boolean[m][n];
vis[ball[0]][ball[1]] = true;
dfs(ball[0], ball[1], maze, hole, vis, "", 0);
return res == null ? "impossible" : res;
}
private void dfs(int i, int j, int[][] maze, int[] hole, boolean[][] vis, String route, int step) {
if (step > minStep) return;
if (i == hole[0] && j == hole[1]) {
if (step == minStep && route.compareTo(res) < 0) {
res = route;
} else if (step < minStep) {
minStep = step;
res = route;
}
vis[i][j] = false;
return;
}
for (int d = 0; d < 4; d++) {
// roll to the wall
int x = i, y = j;
while (x + dirs[d][0] >= 0 && x + dirs[d][0] < m && y + dirs[d][1] >= 0 && y + dirs[d][1] < n
&& maze[x + dirs[d][0]][y + dirs[d][1]] != 1) {
x += dirs[d][0];
y += dirs[d][1];
if (x == hole[0] && y == hole[1] || vis[x][y]) break;
}
if (!vis[x][y] && maze[x][y] == 0) {
vis[x][y] = true;
dfs(x, y, maze, hole, vis, route + dirc[d], step + Math.abs(x - i) + Math.abs(y - j));
vis[x][y] = false;
}
}
}