Massive Algorithms: LeetCode 494

LeetCode 494 - Target Sum

https://leetcode.com/problems/target-sum/

You are given a list of non-negative integers, a1, a2, ..., an, and a target, S. Now you have 2 symbols + and -. For each integer, you should choose one from + and - as its new symbol.

Find out how many ways to assign symbols to make sum of integers equal to target S.

Example 1:

Input: nums is [1, 1, 1, 1, 1], S is 3. 
Output: 5
Explanation: 

-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3

There are 5 ways to assign symbols to make the sum of nums be target 3.

Note:

The length of the given array is positive and will not exceed 20.
The sum of elements in the given array will not exceed 1000.
Your output answer is guaranteed to be fitted in a 32-bit integer.

http://bookshadow.com/weblog/2017/01/22/leetcode-target-sum/

X. 动态规划（Dynamic Programming）

状态转移方程：dp[i + 1][k + nums[i] * sgn] += dp[i][k]

上式中，sgn取值±1，k为dp[i]中保存的所有状态；初始令dp[0][0] = 1

利用滚动数组，可以将空间复杂度优化到O(n)，n为可能的运算结果的个数

http://zhongshutime.com/2017/leetcode_494/


public int findTargetSumWays(int[] nums, int S) {

int sum = 0;

for(int i = 0 ; i < nums.length; i++){

sum += nums[i];

nums[i] <<= 1;

}

if(S > sum) return 0;

return find(nums, S + sum);

}

public int find(int[] nums, int S) {

int[][] dp = new int[nums.length + 1][S + 1];

dp[0][0] = 1;

for(int i = 1; i <= nums.length; i++) {

for(int j = 0; j <= S; j++) {

dp[i][j] = dp[i - 1][j];

int now = nums[i - 1];

if(j - now >= 0)dp[i][j] += dp[i - 1][j - now];

}

}

return dp[nums.length][S];

}

http://www.cnblogs.com/grandyang/p/6395843.html
我们也可以使用迭代的方法来解，还是要用dp数组，其中dp[i][j]表示到第i-1个数字且和为j的情况总数

    int findTargetSumWays(vector<int>& nums, int S) {
        int n = nums.size();
        vector<unordered_map<int, int>> dp(n + 1);
        dp[0][0] = 1;
        for (int i = 0; i < n; ++i) {
            for (auto &a : dp[i]) {
                int sum = a.first, cnt = a.second;
                dp[i + 1][sum + nums[i]] += cnt;
                dp[i + 1][sum - nums[i]] += cnt;
            }
        }
        return dp[n][S];
    }

http://www.wonter.net/archives/1101.html

定义dp[i][j]:=dp[i][j]:=前i个数构成j有多少种方案

然后枚举第i个数前面放+还是-

dp[i][j] = dp[i - 1][j - a[i]] + dp[i - 1][j + a[i]]dp[i][j]=dp[i−1][j−a[i]]+dp[i−1][j+a[i]]

为了节省空间可以使用滚动数组

而且注意到数字可能为负数，所以我们可以让所有数字向右偏移1000，也就是-1000看作0，-999看作1，0看作1000，999看作1999，1000看作2000等等

之后见leetcode上有更巧妙的方法可以避免负数的情况，因为如果没有负数的话，我们则可以直接使用背包来求解，时间和空间上都会更好

大致思路如下：

我们假设数字前面为’+’的集合为a，数字前面为’-‘的集合为b，sum(a)为选的正数的累加和，sum(b)为选了负数的数字累加和

则S = sum(a) - sum(b)S=sum(a)−sum(b)

我们两边同时累加sum(a) + sum(b)sum(a)+sum(b)得到：sum(a) + sum(b) + S = sum(a) - sum(b) + sum(a) + sum(b)sum(a)+sum(b)+S=sum(a)−sum(b)+sum(a)+sum(b)

化简得到：S + sum(a) + sum(b) = 2 * sum(a)S+sum(a)+sum(b)=2∗sum(a)

这里的sum(a) + sum(b)sum(a)+sum(b)则是整个数组的和，所以我们得到了一个新的newS：\frac{newS}{2} = sum(a)​2​​newS​​=sum(a)

也就是得到了一个新的问题：选出若干数的和为newS有多少种方案，而且这里的每个数都是正数。newS则是S + 所有数字之和，并且注意到newS为偶数时才有解。

LeetCode之494. Target Sum思路.
http://blog.csdn.net/gqk289/article/details/54709004
https://leetcode.com/problems/target-sum/discuss/97439/Easily-understood-solution-in-8-lines

内层循环要用next数组保存下一状态，如果都用dp保存的话，下一状态对于当前未遍历到的状态会有污染。

public int findTargetSumWays(int[] nums, int s) {
int sum = 0;
for(int i: nums) sum+=i;
if(s>sum || s<-sum) return 0;
int[] dp = new int[2*sum+1];
dp[0+sum] = 1;
for(int i = 0; i<nums.length; i++){
int[] next = new int[2*sum+1];
for(int k = 0; k<2*sum+1; k++){
if(dp[k]!=0){
next[k + nums[i]] += dp[k];
next[k - nums[i]] += dp[k];
}
}
dp = next;
}
return dp[sum+s];
}

https://leetcode.com/articles/target-sum/

    public int findTargetSumWays(int[] nums, int S) {
        int[][] dp = new int[nums.length][2001];
        dp[0][nums[0] + 1000] = 1;
        dp[0][-nums[0] + 1000] += 1;
        for (int i = 1; i < nums.length; i++) {
            for (int sum = -1000; sum <= 1000; sum++) {
                if (dp[i - 1][sum + 1000] > 0) {
                    dp[i][sum + nums[i] + 1000] += dp[i - 1][sum + 1000];
                    dp[i][sum - nums[i] + 1000] += dp[i - 1][sum + 1000];
                }
            }
        }
        return S > 1000 ? 0 : dp[nums.length - 1][S + 1000];
    }

X.SubSet Sum
https://kingsfish.github.io/2017/08/22/Leetcode-494-Target-Sum/

假设数组中所有数字之和为sum。根据使用的符号不同，我们可以将数组内数字分为2组P和N，如数组{1,2,3}，目标为0，那么显然有如下选择方式：

+1+2-3 = 0

那么其中P={1,2}，N={3}。那么sum(P)-sum(N)=S，并且sum(P)+sum(N)=sum。由此可以推出S+sum=sum(P)-sum(N)+sum(P)+sum(N)=2*sum(P)。

这样我们就把原来的问题转换成了一个新的问题，在整个数组中，能否找到一些数字的和为(S+sum)/2，这就成了一个最经典的0-1背包问题，这样的话就简单了很多。

这里有一个需要注意的地方，(S+sum)/2这个数必须为偶数，否则无法得到，其次，S也必须小于sum，否则也无法求得。

这个算法的空间复杂度不定，取决于S和sum，不过题目限制了sum < 1000，那么空间复杂度为O(sum)。至于时间复杂度也取决于sum，时间复杂度是O(sum*N²)


public int findTargetSumWays(int[] nums, int S) {

    int sum = 0;

    for (int i = 0; i < nums.length; i ++){

        sum += nums[i];

    }

    if (S > sum || (S + sum) % 2 != 0){

        return 0;

    }

    sum = (S + sum) / 2;

    int [] dp = new int[sum + 1];

    dp[0] = 1;

    for (int i = 0; i < nums.length; i ++){

        for (int j = sum; j >= nums[i]; j --){

            dp[j] += dp[j - nums[i]];

        }

    }

    return dp[sum];

}

https://leetcode.com/problems/target-sum/discuss/97335/Short-Java-DP-Solution-with-Explanation

this is a classic knapsack problem
in knapsack, we decide whether we choose this element or not
in this question, we decide whether we add this element or minus it

So start with a two dimensional array dp[i][j] which means the number of ways for first i-th element to reach a sum j

we can easily observe that dp[i][j] = dp[i-1][j+nums[i]] + dp[i-1][j-nums[i],

Another part which is quite confusing is return value, here we return dp[sum+S], why is that?
because dp's range starts from -sum --> 0 --> +sum
so we need to add sum first, then the total starts from 0, then we add S

Actually most of Sum problems can be treated as knapsack problem, hope it helps

    public int findTargetSumWays(int[] nums, int s) {
        int sum = 0; 
        for(int i: nums) sum+=i;
        if(s>sum || s<-sum) return 0;
        int[] dp = new int[2*sum+1];
        dp[0+sum] = 1;
        for(int i = 0; i<nums.length; i++){
            int[] next = new int[2*sum+1];
            for(int k = 0; k<2*sum+1; k++){
                if(dp[k]!=0){
                    next[k + nums[i]] += dp[k];
                    next[k - nums[i]] += dp[k];
                }
            }
            dp = next;
        }
        return dp[sum+s];
    }

https://blog.csdn.net/mine_song/article/details/70216562
1、该问题求解数组中数字只和等于目标值的方案个数，每个数字的符号可以为正或负(减整数等于加负数)。

2、该问题和矩阵链乘很相似，是典型的动态规划问题

3、举例说明: nums = {1,2,3,4,5}, target=3, 一种可行的方案是+1-2+3-4+5 = 3

该方案中数组元素可以分为两组，一组是数字符号为正(P={1,3,5})，另一组数字符号为负(N={2,4})

因此: sum(1,3,5) - sum(2,4) = target

sum(1,3,5) - sum(2,4) + sum(1,3,5) + sum(2,4) = target + sum(1,3,5) + sum(2,4)

2sum(1,3,5) = target + sum(1,3,5) + sum(2,4)

2sum(P) = target + sum(nums)

sum(P) = (target + sum(nums)) / 2

由于target和sum(nums)是固定值，因此原始问题转化为求解nums中子集的和等于sum(P)的方案个数问题

4、求解nums中子集合只和为sum(P)的方案个数(nums中所有元素都是非负)

该问题可以通过动态规划算法求解

举例说明：给定集合nums={1,2,3,4,5}, 求解子集，使子集中元素之和等于9 = new_target = sum(P) = (target+sum(nums))/2

定义dp[10]数组, dp[10] = {1,0,0,0,0,0,0,0,0,0}

dp[i]表示子集合元素之和等于当前目标值的方案个数, 当前目标值等于9减去当前元素值

当前元素等于1时，dp[9] = dp[9] + dp[9-1]

dp[8] = dp[8] + dp[8-1]

...

dp[1] = dp[1] + dp[1-1]

当前元素等于2时，dp[9] = dp[9] + dp[9-2]

dp[8] = dp[8] + dp[8-2]

...

dp[2] = dp[2] + dp[2-2]

当前元素等于3时，dp[9] = dp[9] + dp[9-3]

dp[8] = dp[8] + dp[8-3]

...

dp[3] = dp[3] + dp[3-3]

当前元素等于4时，

...

当前元素等于5时，

...

dp[5] = dp[5] + dp[5-5]

最后返回dp[9]即是所求的解
http://bgmeow.xyz/2017/01/29/LeetCode-494/

它将题目简化为，将 nums 分成一个正数集合 P 与一个负数集合 N ，使 sum(P) - sum(N) = target。更厉害转化在下面：


sum(P) - sum(N) = target

sum(P) + sum(N) + sum(P) - sum(N) = target + sum(P) + sum(N)

2 * sum(P) = target + sum(nums)

sum(P) = (target + sum(nums)) / 2

这就变成了在 nums 中找和为 (target + sum(nums)) / 2 的集合个数，这就是一个背包！
状态方程为 dp[sum] = dp[sum - nums[i]] + dp[nums[i]]

而且 (target + sum(nums)) 一定是偶数。

时间复杂度为

O (N S)


public int findTargetSumWays(int[] nums, int s) {

int sum = 0;

for (int n : nums)

sum += n;

return sum < s || (s + sum) % 2 > 0 ? 0 : subsetSum(nums, (s + sum) >>> 1); 

}   



public int subsetSum(int[] nums, int s) {

int[] dp = new int[s + 1]; 

dp[0] = 1;

for (int n : nums)

for (int i = s; i >= n; i--)

dp[i] += dp[i - n]; 

return dp[s];

}

https://discuss.leetcode.com/topic/76243/java-15-ms-c-3-ms-o-ns-iterative-dp-solution-using-subset-sum-with-explanation

The recursive solution is very slow, because its runtime is exponential

The original problem statement is equivalent to:
Find a subset of nums that need to be positive, and the rest of them negative, such that the sum is equal to target

Let P be the positive subset and N be the negative subset
For example:
Given nums = [1, 2, 3, 4, 5] and target = 3 then one possible solution is +1-2+3-4+5 = 3
Here positive subset is P = [1, 3, 5] and negative subset is N = [2, 4]

Then let's see how this can be converted to a subset sum problem:

                  sum(P) - sum(N) = target
sum(P) + sum(N) + sum(P) - sum(N) = target + sum(P) + sum(N)
                       2 * sum(P) = target + sum(nums)

So the original problem has been converted to a subset sum problem as follows:
Find a subset P of nums such that sum(P) = (target + sum(nums)) / 2

Note that the above formula has proved that target + sum(nums) must be even
We can use that fact to quickly identify inputs that do not have a solution (Thanks to @BrunoDeNadaiSarnaglia for the suggestion)
For detailed explanation on how to solve subset sum problem, you may refer to Partition Equal Subset Sum

Since it is transformed to a subset problem where the target sum can be compose of a sum of even numbers, we could add a simple if testing S + sum to be even.

    public int findTargetSumWays(int[] nums, int s) {
        int sum = 0;
        for (int n : nums)
            sum += n;
        return sum < s || (s + sum) % 2 > 0 ? 0 : subsetSum(nums, (s + sum) >>> 1); 
    }   

    public int subsetSum(int[] nums, int s) {
        int[] dp = new int[s + 1]; 
        dp[0] = 1;
        for (int n : nums)
            for (int i = s; i >= n; i--)
                dp[i] += dp[i - n]; 
        return dp[s];
    }

The DP part is almost the same problem as Partition Equal Subset Sum It is also a subset sum problem

    int findTargetSumWays(vector<int>& nums, int S) {
        unordered_map<int, int> dp;
        dp[0] = 1;
        for (int num : nums) {
            unordered_map<int, int> t;
            for (auto a : dp) {
                int sum = a.first, cnt = a.second;
                t[sum + num] += cnt;
                t[sum - num] += cnt;
            }
            dp = t;
        }
        return dp[S];
    }

http://blog.csdn.net/mine_song/article/details/70216562

X. DP
https://leetcode.com/problems/target-sum/discuss/223661/Using-Map-java-Dp-solution

public int findTargetSumWays(int[] nums, int S) {
    Map<Integer,Integer> map = new HashMap<>();
    if( nums[0] == 0 )
        map.put( 0 , 2 );
    else
    { 
        map.put( -nums[0] , 1 );
        map.put( nums[0] , 1 );
    }
    
    for( int i = 0; i < nums.length ; i++  )
    {
        int num = nums[i];
        ArrayList<Integer> tmp = new ArrayList<>(map.keySet() );
        Map<Integer,Integer> newMap = new HashMap<>();
    for( int a : tmp )
    {
        int ocr1 = newMap.getOrDefault( a - num , 0 );
        newMap.put( a - num , map.get(a) + ocr1 );
        int ocr2 = newMap.getOrDefault( a + num , 0);
        newMap.put( a + num , map.get(a) + ocr2 );
    }
        map = newMap;
    }

    
    return map.getOrDefault( S , 0 );
}

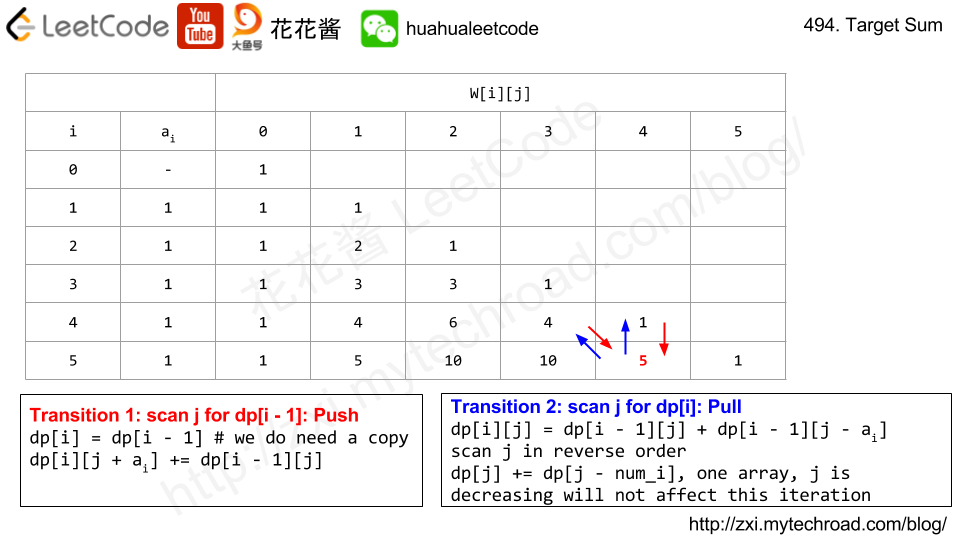
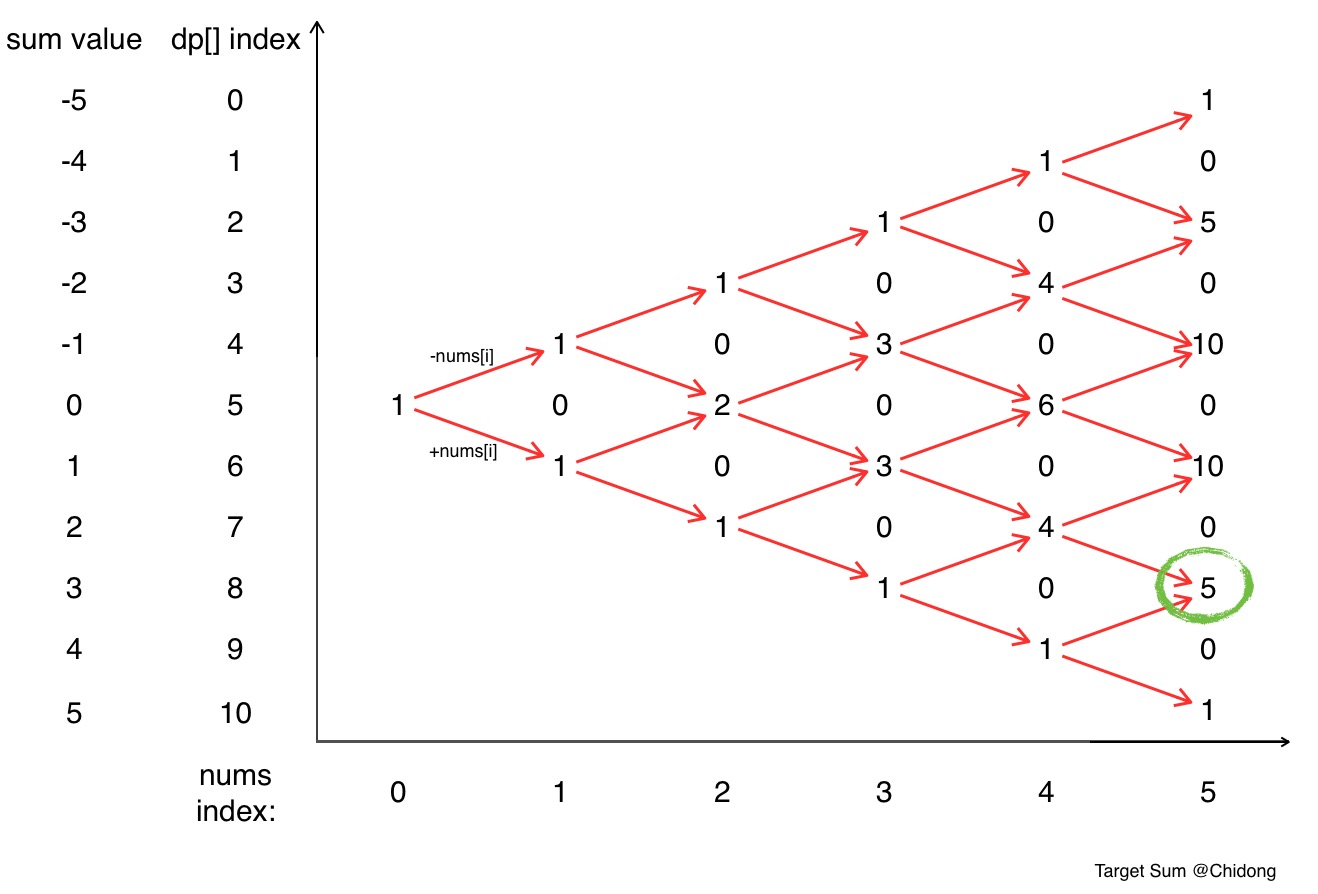
https://lina.bitcron.com/post/code/targetsum
https://zxi.mytechroad.com/blog/dynamic-programming/leetcode-494-target-sum/

Time complexity: O(n*sum)

   public int findTargetSumWays(int[] nums, int S) {
           //注释(1)
         if(nums.length==0)return 0;
           int sum = 0;
         for(int i:nums)  {sum+=i;}

           if(S>sum||S+sum<0)return 0;  //important!!! 没有这一行会导致数组 nullOfPointerException

           int len = sum*2+1;
           int count[] = new int[len];
           count[nums[0]+sum]++;
           count[sum-nums[0]]++;
           for(int i = 1;i<nums.length;i++){
             int next[] = new int[len];            //注释（2）  pay attention
             for(int j = 0;j<len;j++){
                    if(count[j]>0){
                        next[j+nums[i]]+=count[j];
                        next[j-nums[i]]+=count[j];
                    }
               }
              count = next;
             }

          return count[S+sum];
       }

(1)虽然遍历 count[]也很傻比，但是sum的range 是(-1000,1000),那么count的长度最多也才2000，可是DFS遍历，最多有2^20的情况需要access. Way better! 这就是DP的魅力，换个维度处理问题虽然没有到非常简单，但比DFS cheaper,只是代码写起来麻烦点。为什么DP可以简化那么多，因为2^20种求和方式里有很多重合的和。时间O(KN),空间O(KN)(2)为什么要new新数组，首先我不希望第三个num被处理的时候，会和第一个num的和求和，我们只能和第二个num的和求和，所以本质上数组要清空上一次的留下这次的（类似BFS里的QUEUE），如果我们只是在访问过count[j]把它清空，再接着iteration又会有问题，就是每次访问是会修改count[]后面的值的，也就是说后面的num还会和自己的sum求和（不合逻辑），本来想一个机制来保护不被访问后来想了一下基本不可能，因为我们不知道旧数据具体在哪。那么这就说明当前num得到的一些和要放到iteration access不了的地方，=>新数组~既可以清空历史痕迹，也可以保护新数据

DP: O(sum) space

  public int findTargetSumWays(int[] nums, int S) {

    int sum = 0;

    for (final int num : nums)

      sum += num;

    if (sum < S) return 0;

    final int kOffset = sum;

    final int kMaxN = sum * 2 + 1;

    int[] ways = new int[kMaxN];

    ways[kOffset] = 1;

    for (final int num : nums) {      

      int[] tmp = new int[kMaxN];      

      for (int i = num; i < kMaxN - num; ++i) {

        tmp[i + num] += ways[i];

        tmp[i - num] += ways[i];

}

      ways = tmp;

}

    return ways[S + kOffset];

}

X. DP with map
http://www.cnblogs.com/grandyang/p/6395843.html
我们也可以对上面的方法进行空间上的优化，只用一个哈希表，而不是用一个数组的哈希表，我们在遍历数组中的每一个数字时，新建一个哈希表，我们在遍历原哈希表中的项时更新这个新建的哈希表，最后把新建的哈希表整个赋值和原哈希表

    int findTargetSumWays(vector<int>& nums, int S) {
        unordered_map<int, int> dp;
        dp[0] = 1;
        for (int num : nums) {
            unordered_map<int, int> t;
            for (auto a : dp) {
                int sum = a.first, cnt = a.second;
                t[sum + num] += cnt;
                t[sum - num] += cnt;
            }
            dp = t;
        }
        return dp[S];
    }

X. DFS+Memorization
http://guoyc.com/post/target_sum/


public int findTargetSumWays(int[] nums, int S) {

return dp(nums, nums.length-1, S, new HashMap<>());

}

public int dp(int[] nums, int i, int target, Map<String, Integer> memo) {

if (i==-1) {

return target==0?1:0;

}

String key = String.valueOf(i)+','+String.valueOf(target);

if (!memo.containsKey(key)) {

memo.put(key, dp(nums, i-1, target+nums[i], memo)+dp(nums, i-1, target-nums[i], memo));

}

return memo.get(key);

}

https://leetcode.com/articles/target-sum/

It can be easily observed that in the last approach, a lot of redundant function calls could be made with the same value of

i

as the current index and the same value of

sum

as the current sum, since the same values could be obtained through multiple paths in the recursion tree. In order to remove this redundancy, we make use of memoization as well to store the results which have been calculated earlier.

Thus, for every call to calculate(nums, i, sum, S), we store the result obtained in

memo[i][sum + 1000]

. The factor of 1000 has been added as an offset to the

sum

value to map all the

sum

s possible to positive integer range. By making use of memoization, we can prune the search space to a good extent.

Time complexity : $O(l*n)$ . The $memo$ array of size $l*n$ has been filled just once. Here, $l$ refers to the range of $sum$ and $n$ refers to the size of $nums$ array.
Space complexity : $O(n)$ . The depth of recursion tree can go upto $n$ .

https://leetcode.com/problems/target-sum/discuss/97333/Java-simple-DFS-with-memorization
I used a map to record the intermediate result while we are walking along the recursion tree.

    public int findTargetSumWays(int[] nums, int S) {
        if (nums == null || nums.length == 0){
            return 0;
        }
        return helper(nums, 0, 0, S, new HashMap<>());
    }
    private int helper(int[] nums, int index, int sum, int S, Map<String, Integer> map){
        String encodeString = index + "->" + sum;
        if (map.containsKey(encodeString)){
            return map.get(encodeString);
        }
        if (index == nums.length){
            if (sum == S){
                return 1;
            }else {
                return 0;
            }
        }
        int curNum = nums[index];
        int add = helper(nums, index + 1, sum - curNum, S, map);
        int minus = helper(nums, index + 1, sum + curNum, S, map);
        map.put(encodeString, add + minus);
        return add + minus;
    }

http://shibaili.blogspot.com/2018/07/494-target-sum.html

https://leetcode.com/articles/target-sum/

    int count = 0;
    public int findTargetSumWays(int[] nums, int S) {
        int[][] memo = new int[nums.length][2001];
        for (int[] row: memo)
            Arrays.fill(row, Integer.MIN_VALUE);
        return calculate(nums, 0, 0, S, memo);
    }
    public int calculate(int[] nums, int i, int sum, int S, int[][] memo) {
        if (i == nums.length) {
            if (sum == S)
                return 1;
            else
                return 0;
        } else {
            if (memo[i][sum + 1000] != Integer.MIN_VALUE) {
                return memo[i][sum + 1000];
            }
            int add = calculate(nums, i + 1, sum + nums[i], S, memo);
            int subtract = calculate(nums, i + 1, sum - nums[i], S, memo);
            memo[i][sum + 1000] = add + subtract;
            return memo[i][sum + 1000];
        }
    }

X. Prune
https://leetcode.com/problems/target-sum/discuss/97371/Java-Short-DFS-Solution

Optimization: The idea is

If the sum of all elements left is smaller than absolute value of target, there will be no answer following the current path. Thus we can return.

    int result = 0;
 
    public int findTargetSumWays(int[] nums, int S) {
        if(nums == null || nums.length == 0) return result;
        
        int n = nums.length;
        int[] sums = new int[n];
        sums[n - 1] = nums[n - 1];
        for (int i = n - 2; i >= 0; i--)
            sums[i] = sums[i + 1] + nums[i];
        
        helper(nums, sums, S, 0);
        return result;
    }
    public void helper(int[] nums, int[] sums, int target, int pos){
        if(pos == nums.length){
            if(target == 0) result++;
            return;
        }
        
        if (sums[pos] < Math.abs(target)) return;
        
        helper(nums, sums, target + nums[pos], pos + 1);
        helper(nums, sums, target - nums[pos], pos + 1);
    }

X. DFS
https://discuss.leetcode.com/topic/76201/java-short-dfs-solution
http://rainykat.blogspot.com/2017/01/leetcodegf-494-target-sum-dfs.html
思路： use dfs to find travel the array, each number have 2 opitons: '+' and '-'
Complexity: O(2^n)

    public int findTargetSumWays(int[] nums, int S) {
        if(nums == null)return 0;
        return dfs(nums, S, 0, 0);
    }
    public int dfs(int[] nums, int S, int index, int sum){
        int res = 0;
        if(index == nums.length){
            if(sum == S) res++;
            return res;
        }
        res += dfs(nums, S, index + 1, sum + nums[index]);
        res += dfs(nums, S, index + 1, sum - nums[index]);
        return res;
    }

If the sum of all elements left is smaller than absolute value of target, there will be no answer following the current path. Thus we can return.

    public int findTargetSumWays(int[] nums, int S) {
        if(nums == null)return 0;
        int n = nums.length;
        int[] sums = new int[n];
        sums[n-1] = nums[n-1];
        for(int i = n-2; i >= 0; i--){
            sums[i] = nums[i] + sums[i+1];
        }
        return dfs(nums, sums, S, 0, 0);
    }
    public int dfs(int[] nums, int[] sums, int S, int index, int sum){
        int res = 0;
        if(index == nums.length){
            if(sum == S) res++;
            return res;
        }
        if(sums[index] < Math.abs(S - sum))return 0;
        res += dfs(nums, sums, S, index + 1, sum + nums[index]);
        res += dfs(nums, sums, S, index + 1, sum - nums[index]);
        return res;
    }

https://discuss.leetcode.com/topic/76361/backtracking-solution-java-easy

    public int findTargetSumWays(int[] nums, int S) {
        int sum = 0;
        int[] arr = new int[1];
        helper(nums, S, arr,0,0);
        return arr[0];
    }
    
    public void helper(int[] nums, int S, int[] arr,int sum, int start){
        if(start==nums.length){
            if(sum == S){
                arr[0]++;
            }
            return;
        }
            //这里千万不要加for循环，因为我们只是从index0开始
            helper(nums,S,arr,sum-nums[start],start+1);
            helper(nums,S,arr,sum+nums[start],start+1);
        
    }

X. https://discuss.leetcode.com/topic/76264/short-java-dp-solution-with-explanation

    public int findTargetSumWays(int[] nums, int s) {
        int sum = 0; 
        for(int i: nums) sum+=i;
        if(s>sum || s<-sum) return 0;
        int[] dp = new int[2*sum+1];
        dp[0+sum] = 1;
        for(int i = 0; i<nums.length; i++){
            int[] next = new int[2*sum+1];
            for(int k = 0; k<2*sum+1; k++){
                if(dp[k]!=0){
                    next[k + nums[i]] += dp[k];
                    next[k - nums[i]] += dp[k];
                }
            }
            dp = next;
        }
        return dp[sum+s];
    }

0_1485048724190_Screen Shot 2017-01-21 at 8.31.48 PM.jpg

X. https://leetcode.com/articles/target-sum/
Approach #1 Brute Force [Accepted]

Time complexity : $O(2^n)$ . Size of recursion tree will be $2^n$ . $n$ refers to the size of $nums$ array.

int count = 0;

public int findTargetSumWays(int[] nums, int S) {

calculate(nums, 0, 0, S);

return count;

}

public void calculate(int[] nums, int i, int sum, int S) {

if (i == nums.length) {

if (sum == S)

count++;

} else {

calculate(nums, i + 1, sum + nums[i], S);

calculate(nums, i + 1, sum - nums[i], S);

}

http://guoyc.com/post/target_sum/

LeetCode 494 - Target Sum

Labels

Popular Posts