https://leetcode.com/problems/minimum-cost-for-tickets/
https://leetcode.com/problems/minimum-cost-for-tickets/discuss/226659/Two-DP-solutions-with-pictures
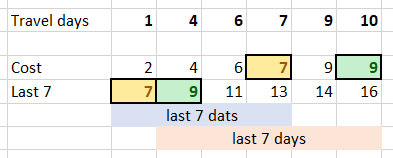
Approach 2: Dynamic Programming (Window Variant)
https://www.acwing.com/solution/LeetCode/content/877/
状态 f(i)f(i) 表示满足了前 ii 个日期的最少花费。日期下标从 1 开始。
初始值 f(0)=0f(0)=0,其余为正无穷。可以想到,每次买票一定选在在某个存在的日期。
状态转移,f(i)=min(f(j)+cost(k))f(i)=min(f(j)+cost(k)),其中 jj 表示上一个买票的日期,kk 表示对应的价钱。倒序枚举 jj,如果两个日期差距大于等于 30 天,则无需继续枚举。
最终答案为 f(n)f(n)。
时间复杂度
状态数为 O(n)O(n) 个,注意到每次转移最多只要 30 个,故总时间复杂度为 O(n)O(n)
int mincostTickets(vector<int>& days, vector<int>& costs) {
int n = days.size();
vector<int> f(n + 1, INT_MAX);
f[0] = 0;
days.insert(days.begin(), 0);
for (int i = 1; i <= n; i++) {
for (int j = i; j >= 1; j--) {
if (days[i] - days[j] < 1)
f[i] = min(f[i], f[i - 1] + costs[0]);
if (days[i] - days[j] < 7)
f[i] = min(f[i], f[j - 1] + costs[1]);
if (days[i] - days[j] < 30)
f[i] = min(f[i], f[j - 1] + costs[2]);
if (days[i] - days[j] >= 30)
break;
}
}
return f[n];
}
X. DP + two pointers/sliding window
https://blog.csdn.net/mike_learns_to_rock/article/details/86669196
X.
https://leetcode.com/problems/minimum-cost-for-tickets/discuss/226659/Two-DP-solutions-with-pictures

Approach 1: Dynamic Programming (Day Variant)
https://leetcode.com/problems/minimum-cost-for-tickets/discuss/226670/Java-DP-Solution-with-explanation-O(n)
https://leetcode.com/problems/minimum-cost-for-tickets/discuss/226704/Java-O(nlogn)-DP-solution-and-recursion-%2B-memorization-solution
In a country popular for train travel, you have planned some train travelling one year in advance. The days of the year that you will travel is given as an array
days. Each day is an integer from 1 to 365.
Train tickets are sold in 3 different ways:
- a 1-day pass is sold for
costs[0]dollars; - a 7-day pass is sold for
costs[1]dollars; - a 30-day pass is sold for
costs[2]dollars.
The passes allow that many days of consecutive travel. For example, if we get a 7-day pass on day 2, then we can travel for 7 days: day 2, 3, 4, 5, 6, 7, and 8.
Return the minimum number of dollars you need to travel every day in the given list of
days.
Example 1:
Input: days = [1,4,6,7,8,20], costs = [2,7,15] Output: 11 Explanation: For example, here is one way to buy passes that lets you travel your travel plan: On day 1, you bought a 1-day pass for costs[0] = $2, which covered day 1. On day 3, you bought a 7-day pass for costs[1] = $7, which covered days 3, 4, ..., 9. On day 20, you bought a 1-day pass for costs[0] = $2, which covered day 20. In total you spent $11 and covered all the days of your travel.
Example 2:
Input: days = [1,2,3,4,5,6,7,8,9,10,30,31], costs = [2,7,15] Output: 17 Explanation: For example, here is one way to buy passes that lets you travel your travel plan: On day 1, you bought a 30-day pass for costs[2] = $15 which covered days 1, 2, ..., 30. On day 31, you bought a 1-day pass for costs[0] = $2 which covered day 31. In total you spent $17 and covered all the days of your travel.
Note:
1 <= days.length <= 3651 <= days[i] <= 365daysis in strictly increasing order.costs.length == 31 <= costs[i] <= 1000
https://leetcode.com/problems/minimum-cost-for-tickets/discuss/226659/Two-DP-solutions-with-pictures
The higher is the bar, the more you're expected to use dynamic programming (DP) during an interview. This technique requires a lot of practice to grasp; if you've mastered the recursion, DP is the next level.
2. Track travel days
We track the minimum
cost for each travel day. We process only travel days and store {day, cost} for 7-and 30-day passes in the last7 and last30 queues. After a pass 'expires', we remove it from the queue. This way, our queues only contains travel days for the last 7 and 30 days, and the cheapest pass prices are in the front of the queues.
int mincostTickets(vector<int>& days, vector<int>& costs, int cost = 0) {
queue<pair<int, int>> last7, last30;
for (auto d : days) {
while (!last7.empty() && last7.front().first + 7 <= d) last7.pop();
while (!last30.empty() && last30.front().first + 30 <= d) last30.pop();
last7.push({ d, cost + costs[1] });
last30.push({ d, cost + costs[2] });
cost = min({ cost + costs[0], last7.front().second, last30.front().second });
}
return cost;
}
Complexity analysis
- Time Complexity: O(n), where n is the number of travel days.
- Space Complexity: O(38). Stricter, it's a sum of duration for all pass types (1 + 7 + 30 in our case)
Approach 2: Dynamic Programming (Window Variant)
As in Approach 1, we only need to buy a travel pass on a day we intend to travel.
Now, let
dp(i) be the cost to travel from day days[i] to the end of the plan. If say, j1 is the largest index such that days[j1] < days[i] + 1, j7 is the largest index such that days[j7] < days[i] + 7, and j30 is the largest index such that days[j30] < days[i] + 30, then we have:- Time Complexity: , where is the number of unique days in your travel plan.
- Space Complexity: .
int[] days, costs;
Integer[] memo;
int[] durations = new int[] { 1, 7, 30 };
public int mincostTickets(int[] days, int[] costs) {
this.days = days;
this.costs = costs;
memo = new Integer[days.length];
return dp(0);
}
public int dp(int i) {
if (i >= days.length)
return 0;
if (memo[i] != null)
return memo[i];
int ans = Integer.MAX_VALUE;
int j = i;
for (int k = 0; k < 3; ++k) {
while (j < days.length && days[j] < days[i] + durations[k])
j++;
ans = Math.min(ans, dp(j) + costs[k]);
}
memo[i] = ans;
return ans;
}
https://zhanghuimeng.github.io/post/leetcode-983-minimum-cost-for-tickets/int mincostTickets(vector<int>& days, vector<int>& costs) { int f[365]; int N = days.size(); for (int i = 0; i < N; i++) { if (i == 0) { f[0] = min(costs[0], costs[1]); f[0] = min(costs[2], f[0]); continue; } f[i] = f[i-1] + costs[0]; // 感觉这个转移条件也是有点奇怪…… for (int j = 1; j <= 30 && j <= i; j++) { int x = j < i ? f[i-j-1] : 0; if (days[i] - days[i-j] + 1 <= 7) f[i] = min(f[i], x + costs[1]); if (days[i] - days[i-j] + 1 <= 30) f[i] = min(f[i], x + costs[2]); } } return f[N - 1]; }
https://www.acwing.com/solution/LeetCode/content/877/
状态 f(i)f(i) 表示满足了前 ii 个日期的最少花费。日期下标从 1 开始。
初始值 f(0)=0f(0)=0,其余为正无穷。可以想到,每次买票一定选在在某个存在的日期。
状态转移,f(i)=min(f(j)+cost(k))f(i)=min(f(j)+cost(k)),其中 jj 表示上一个买票的日期,kk 表示对应的价钱。倒序枚举 jj,如果两个日期差距大于等于 30 天,则无需继续枚举。
最终答案为 f(n)f(n)。
时间复杂度
状态数为 O(n)O(n) 个,注意到每次转移最多只要 30 个,故总时间复杂度为 O(n)O(n)
int mincostTickets(vector<int>& days, vector<int>& costs) {
int n = days.size();
vector<int> f(n + 1, INT_MAX);
f[0] = 0;
days.insert(days.begin(), 0);
for (int i = 1; i <= n; i++) {
for (int j = i; j >= 1; j--) {
if (days[i] - days[j] < 1)
f[i] = min(f[i], f[i - 1] + costs[0]);
if (days[i] - days[j] < 7)
f[i] = min(f[i], f[j - 1] + costs[1]);
if (days[i] - days[j] < 30)
f[i] = min(f[i], f[j - 1] + costs[2]);
if (days[i] - days[j] >= 30)
break;
}
}
return f[n];
}
X. DP + two pointers/sliding window
https://blog.csdn.net/mike_learns_to_rock/article/details/86669196
public int mincostTickets(int[] days, int[] costs) {
// dp[i + 1] .. days[0, .., i]的最优解
// dp[i] = min(dp[week] + costs[1], dp[month] + costs[2], dp[i - 1] + costs[0]);
int week = 0;
int month = 0;
int[] dp = new int[days.length + 1];
dp[0] = 0;
for (int i = 0; i < days.length; i++) {
while (days[week] < days[i] - 6) {
week++;
}
while (days[month] < days[i] - 29) {
month++;
}
int tmp = Math.min(dp[i] + costs[0], dp[week] + costs[1]);
dp[i + 1] = Math.min(tmp, dp[month] + costs[2]);
}
return dp[days.length];
}
X.
https://leetcode.com/problems/minimum-cost-for-tickets/discuss/226659/Two-DP-solutions-with-pictures
For each travel day, we can buy a one-day ticket, or use 7-day or 30-day pass as if we would have purchased it 7 or 30 days ago. We need to track rolling costs for at least 30 days back, and use them to pick the cheapest option for the next travel day.
Here, we can use two approaches: track cost for all calendar days, or process only travel days. The first approach is simpler to implement, but it's slower. Since the problem is limited to one calendar year, it does not make much of a difference; for a generalized problem I would recommend the second approach.
1. Track calendar days
We track the minimum cost for all calendar days in
dp. For non-travel days, the cost stays the same as for the previous day. For travel days, it's a minimum of yesterday's cost plus single-day ticket, or cost for 8 days ago plus 7-day pass, or cost 31 days ago plus 30-day pass.
int mincostTickets(vector<int>& days, vector<int>& costs) {
unordered_set<int> travel(begin(days), end(days));
int dp[366] = {};
for (int i = 1; i < 366; ++i) {
if (travel.find(i) == travel.end()) dp[i] = dp[i - 1];
else dp[i] = min({ dp[i - 1] + costs[0], dp[max(0, i - 7)] + costs[1], dp[max(0, i - 30)] + costs[2]});
}
return dp[365];
}
Optimizations
In the previous solution, we store cost for all calendar days. However, since we only look 31 days back, we can just store the cost for last 31 days in a rolling array.
In addition, we can only look at calendar days within our first and last travel dates, as @zengxinhai suggested.
int mincostTickets(vector<int>& days, vector<int>& costs) {
unordered_set<int> travel(begin(days), end(days));
int dp[31] = {};
for (int i = days.front(); i <= days.back(); ++i) {
if (travel.find(i) == travel.end()) dp[i % 31] = dp[(i - 1) % 31];
else dp[i % 31] = min({ dp[(i - 1) % 31] + costs[0],
dp[max(0, i - 7) % 31] + costs[1], dp[max(0, i - 30) % 31] + costs[2] });
}
return dp[days.back() % 31];
}
Complexity analysis
- Time Complexity: O(N), where N is the number of calendar days.
- Space Complexity: O(N) or O(31) for the optimized solution. Stricter, it's a maximum duration among all pass types.
Approach 1: Dynamic Programming (Day Variant)
We can express those choices as a recursion and use dynamic programming. Let's say
dp(i) is the cost to fulfill your travel plan from day i to the end of the plan. Then, if you have to travel today, your cost is:- Time Complexity: , where is the maximum numbered day in your travel plan.
- Space Complexity: .
int[] costs;
Integer[] memo;
Set<Integer> dayset;
public int mincostTickets(int[] days, int[] costs) {
this.costs = costs;
memo = new Integer[366];
dayset = new HashSet();
for (int d : days)
dayset.add(d);
return dp(1);
}
public int dp(int i) {
if (i > 365)
return 0;
if (memo[i] != null)
return memo[i];
int ans;
if (dayset.contains(i)) {
ans = Math.min(dp(i + 1) + costs[0], dp(i + 7) + costs[1]);
ans = Math.min(ans, dp(i + 30) + costs[2]);
} else {
ans = dp(i + 1);
}
memo[i] = ans;
return ans;
}
https://leetcode.com/problems/minimum-cost-for-tickets/discuss/226670/Java-DP-Solution-with-explanation-O(n)
public int mincostTickets(int[] days, int[] costs) {
boolean[] dayIncluded = new boolean[366];
for (int day : days) {
dayIncluded[day] = true;
}
int[] minCost = new int[366];
minCost[0] = 0;
for (int day = 1; day <= 365; ++day) {
if (!dayIncluded[day]) {
minCost[day] = minCost[day-1];
continue;
}
int min;
min = minCost[day-1] + costs[0];
min =Math.min(min, minCost[Math.max(0, day-7)] + costs[1]);
min = Math.min(min, minCost[Math.max(0, day-30)] + costs[2]);
minCost[day] = min;
}
return minCost[365];
}int mincostTickets(vector<int>& days, vector<int>& costs) { int f[366]; f[0] = 0; int i = 0; for (int j = 1; j <= 365; j++) { while (days[i] < j && i < days.size()) i++; if (i < days.size() && j == days[i]) { f[j] = 1e9; // 1 day f[j] = min(f[j], f[j-1] + costs[0]); // 7 days // buy on day f[j-k+1] for (int k = 1; k <= 7 && j - k >= 0; k++) f[j] = min(f[j], f[j-k] + costs[1]); // 30 days for (int k = 1; k <= 30 && j - k >= 0; k++) f[j] = min(f[j], f[j-k] + costs[2]); } else f[j] = f[j-1]; } return f[365]; }X.
https://leetcode.com/problems/minimum-cost-for-tickets/discuss/226704/Java-O(nlogn)-DP-solution-and-recursion-%2B-memorization-solution
public int mincostTickets(int[] days, int[] costs) {
if (days == null || days.length == 0) return 0;
int n = days.length;
int[] dp = new int[n + 1];
for (int i = 0; i < n; i++) {
int res = dp[i] + costs[0]; //previous cost + today's cost...
//find the left most index that is larger than days[i] - 7..
//calculate the cost by using prev cost + one-week cost...
int index7 = binarySearch(days, i, days[i] - 7);
res = Math.min(res, dp[index7] + costs[1]);
//find the left most index that is larger than days[i] - 30..
//calculate the cost by using prev cost + one-month cost...
int index30 = binarySearch(days, i, days[i] - 30);
res = Math.min(res, dp[index30] + costs[2]);
dp[i + 1] = res;
}
return dp[n];
}
private int binarySearch(int[] days, int i, int target) {
int lo = 0, hi = i;
while (lo < hi) {
int mid = lo + (hi - lo) / 2;
if (days[mid] > target) {
hi = mid;
} else {
lo = mid + 1;
}
}
return lo;
}