Related: Minimum number of jumps to reach end
LeetCode 55 - Jump Game
https://leetcode.com/problems/jump-game-ii/




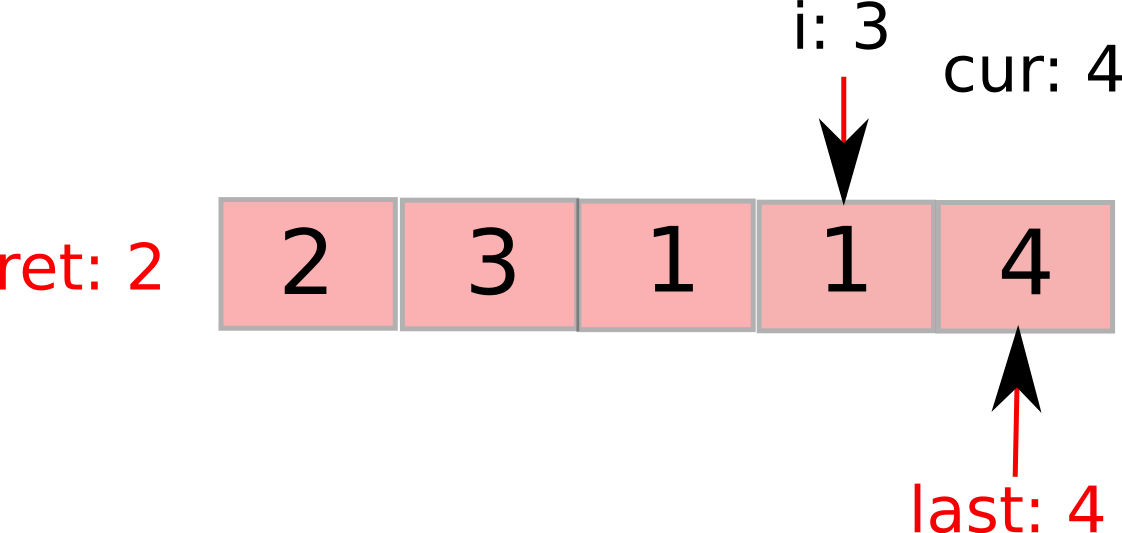
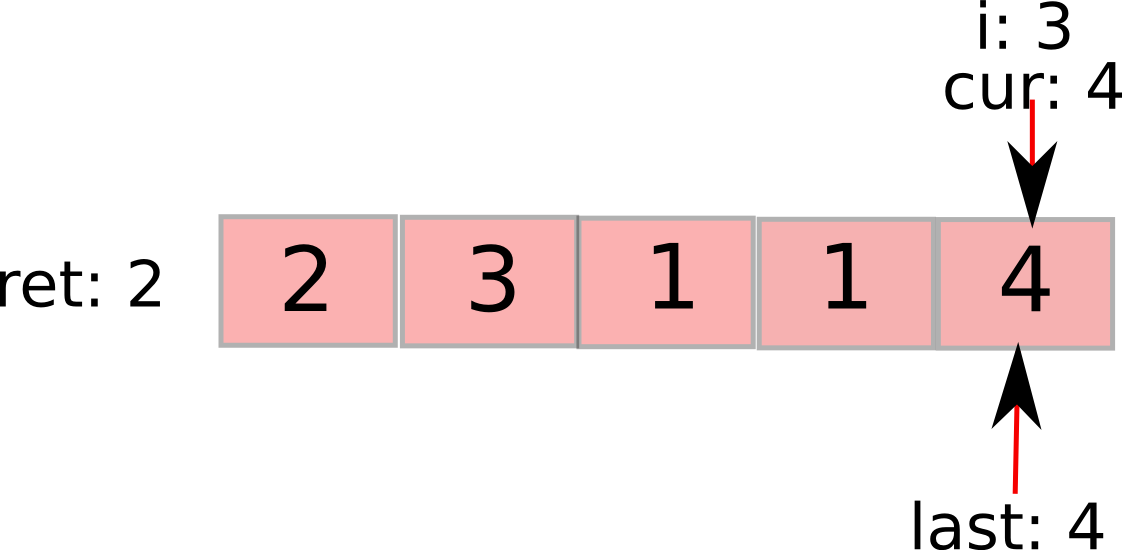 X.
X.
https://leetcode.com/problems/jump-game-ii/discuss/18019/10-lines-C%2B%2B-(16ms)-Python-BFS-Solutions-with-Explanations
I try to change this problem to a BFS problem, where nodes in level i are all the nodes that can be reached in i-1th jump. for example. 2 3 1 1 4 , is
http://fisherlei.blogspot.com/2012/12/leetcode-jump-ii.html
二指针问题,最大覆盖区间。
从左往右扫描,维护一个覆盖区间,每扫过一个元素,就重新计算覆盖区间的边界。比如,开始时区间[start, end], 遍历A数组的过程中,不断计算A[i]+i最大值(即从i坐标开始最大的覆盖坐标),并设置这个最大覆盖坐标为新的end边界。而新的start边界则为原end+1。不断循环,直到end> n.
X. Standard BFS
X. DP
https://www.jiuzhang.com/solution/jump-game-ii/
http://www.cnblogs.com/lichen782/p/leetcode_Jump_Game_II.html
https://fizzbuzzed.com/thinking_through_jump_game_2/


LeetCode 55 - Jump Game
https://leetcode.com/problems/jump-game-ii/
Given an array of non-negative integers, you are initially positioned at the first index of the array.
Each element in the array represents your maximum jump length at that position.
Your goal is to reach the last index in the minimum number of jumps.
Example:
Input: [2,3,1,1,4] Output: 2 Explanation: The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.
Note:
You can assume that you can always reach the last index
http://www.cnblogs.com/grandyang/p/4373533.html
这题是之前那道Jump Game 跳跃游戏 的延伸,那题是问能不能到达最后一个数字,而此题只让我们求到达最后一个位置的最少跳跃数,貌似是默认一定能到达最后位置的? 此题的核心方法是利用贪婪算法Greedy的思想来解,想想为什么呢? 为了较快的跳到末尾,我们想知道每一步能跳的范围,这里贪婪并不是要在能跳的范围中选跳力最远的那个位置,因为这样选下来不一定是最优解,这么一说感觉又有点不像贪婪算法了。我们这里贪的是一个能到达的最远范围,我们遍历当前跳跃能到的所有位置,然后根据该位置上的跳力来预测下一步能跳到的最远距离,贪出一个最远的范围,一旦当这个范围到达末尾时,当前所用的步数一定是最小步数。我们需要两个变量cur和pre分别来保存当前的能到达的最远位置和之前能到达的最远位置,只要cur未达到最后一个位置则循环继续,pre先赋值为cur的值,表示上一次循环后能到达的最远位置,如果当前位置i小于等于pre,说明还是在上一跳能到达的范围内,我们根据当前位置加跳力来更新cur,更新cur的方法是比较当前的cur和i + A[i]之中的较大值,如果题目中未说明是否能到达末尾,我们还可以判断此时pre和cur是否相等,如果相等说明cur没有更新,即无法到达末尾位置,返回-1.
int jump(vector<int>& nums) { int res = 0, n = nums.size(), i = 0, cur = 0; while (cur < n - 1) { ++res; int pre = cur; for (; i <= pre; ++i) { cur = max(cur, i + nums[i]); } if (pre == cur) return -1; // May not need this } return res; }
还有一种写法,跟上面那解法略有不同,但是本质的思想还是一样的,关于此解法的详细分析可参见网友实验室小纸贴校外版的博客,这里cur是当前能到达的最远位置,last是上一步能到达的最远位置,我们遍历数组,首先用i + nums[i]更新cur,这个在上面解法中讲过了,然后判断如果当前位置到达了last,即上一步能到达的最远位置,说明需要再跳一次了,我们将last赋值为cur,并且步数res自增1,这里我们小优化一下,判断如果cur到达末尾了,直接break掉即可
int jump(vector<int>& nums) { int res = 0, n = nums.size(), last = 0, cur = 0; for (int i = 0; i < n - 1; ++i) { cur = max(cur, i + nums[i]); if (i == last) { last = cur; ++res; if (cur >= n - 1) break; } } return res; }
https://www.tianmaying.com/tutorial/LC45
http://www.cnblogs.com/lichen782/p/leetcode_Jump_Game_II.html
https://www.cnblogs.com/ariel-dreamland/p/9139572.html
要理解这个算法,首先明白,这个题只要我们求跳数,怎么跳,最后距离是多少,都没让求的。
看完这道题目,可能大部分的读者都能够想出这样一个相对简单的解法:将每个位置都看作一个点,并从第i个点向它之后的nums[i]个点都连一条长度为1的有向边,而现在的问题就是从0号点到达size-1号点需要的最短距离,这就是一个很简单的最短路问题,实际上由于边的长度均为1,而且不存在环,我们可以用宽度优先搜索(时间复杂度为O(n^2),即边数)来进行相关的计算。
但是这样一道难度为Hard的题会让我们就这么简单通过么?笔者觉得是不会的,所以这题肯定还存在着一些优化。
不难发现,这道题目转换出的最短路问题存在三个条件:
- 边的长度均为1
- 不存在环
- 连出的边是连续的
我们是不是可以用这三个“很强”的条件来做一些优化呢,答案自然是肯定的!
——如果令f[i]表示从0号点到达i号点的最短路径,那么对于任意i<j,有f[i]<=f[j],即f是非递减的,这个结论的证明是显然的,在此不作过多赘述。
在有了这样的结论之后,我们就会发现,其实对于f数组来说,它会是一段段的存在,先是一个0,然后是一段1,然后是一段2,依此类推,那么现在问题来了,每一段的长度是多少呢?
这个问题很好回答,如果我们令l[k]表示f数组中值为k的一段的左边界,r[k]表示f数组中值为k的一段的有边界,那么有
- l[k] = r[k - 1] + 1,这是显然的
- r[k] = max{i + nums[i] | l[k - 1] <= i <= r[k - 1]},由于f值为k的位置一定是从f值为k-1的位置走来的,所以只需要看从所有f值为k-1的位置里最远可以到达的地方即可。
也就是说,我们可以在对nums的一遍扫描中,依次求出所有的l[k]和r[k],而f数组也就自然求解出来了——答案也就得到了。
这道题目虽然在LeetCode上标记为Hard,但是最后得出的解决方法也不算特别的复杂,主要是利用转换后最短路问题的一些特殊性质得到了非常有用的结论,来加速了整个最短路径的计算。
int jump(vector<int>& nums) {
// 初始化l[0], r[0]
int k = 0, l = 0, r = 0;
// 当最后位置的f值没有计算出时保持计算
while (r < nums.size() - 1) {
int next_r = r;
// 遍历l[k]到r[k],计算r[k+1]
for (int i = l; i <= r; i++) next_r = max(next_r, i + nums[i]);
// 替换到k+1,以进行之后的计算
k++; l = r + 1; r = next_r;
}
// 返回最后一个位置的f值
return k;
}
http://www.cnblogs.com/lichen782/p/leetcode_Jump_Game_II.html
https://www.cnblogs.com/ariel-dreamland/p/9139572.html
要理解这个算法,首先明白,这个题只要我们求跳数,怎么跳,最后距离是多少,都没让求的。
大牛这个算法的思想主要是,扫描数组(废话。。。),以确定当前最远能覆盖的节点,放入curr。然后继续扫描,直到当前的路程超过了上一次算出的覆盖范围,那么更新覆盖范围,同时更新条数,因为我们是经过了多一跳才能继续前进的。
形象地说,这个是在争取每跳最远的greedy。举个栗子。
比如就是我们题目中的[2,3,1,1,4]。初始状态是这样的:cur表示最远能覆盖到的地方,用红色表示。last表示已经覆盖的地方,用箭头表示。它们都指在第一个元素上。

接下来,第一元素告诉cur,最远咱可以走2步。于是:

下一循环中,i指向1(图中的元素3),发现,哦,i小于last能到的范围,于是更新last(相当于说,进入了新的势力范围),步数ret加1.同时要更新cur。因为最远距离发现了。

接下来,i继续前进,发现i在当前的势力范围内,无需更新last和步数ret。更新cur。

i继续前进,接下来发现超过当前势力范围,更新last和步数。cur已然最大了。
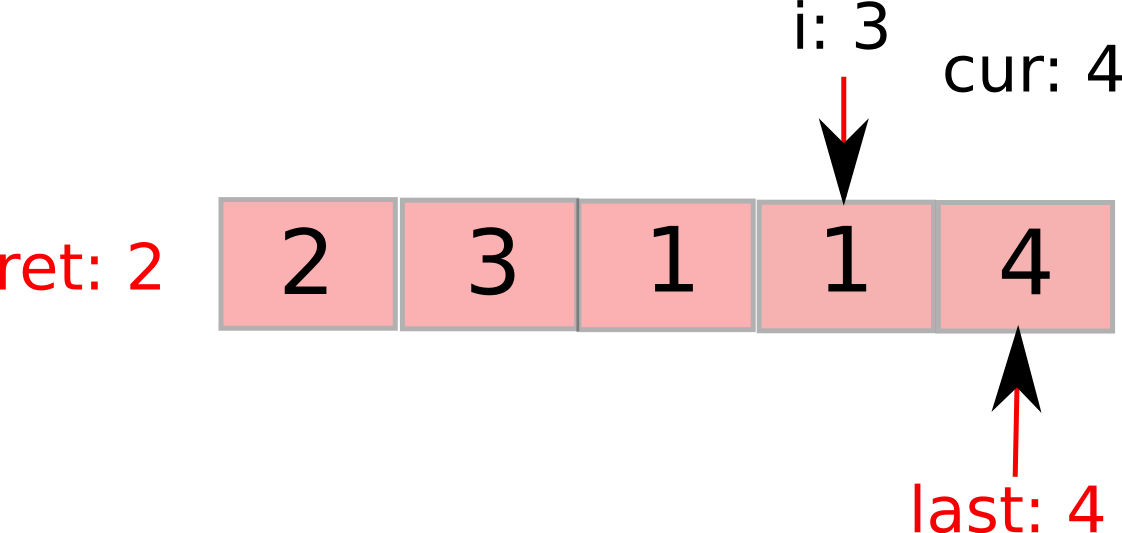
最后,i到最后一个元素。依然在势力范围内,遍历完成,返回ret。
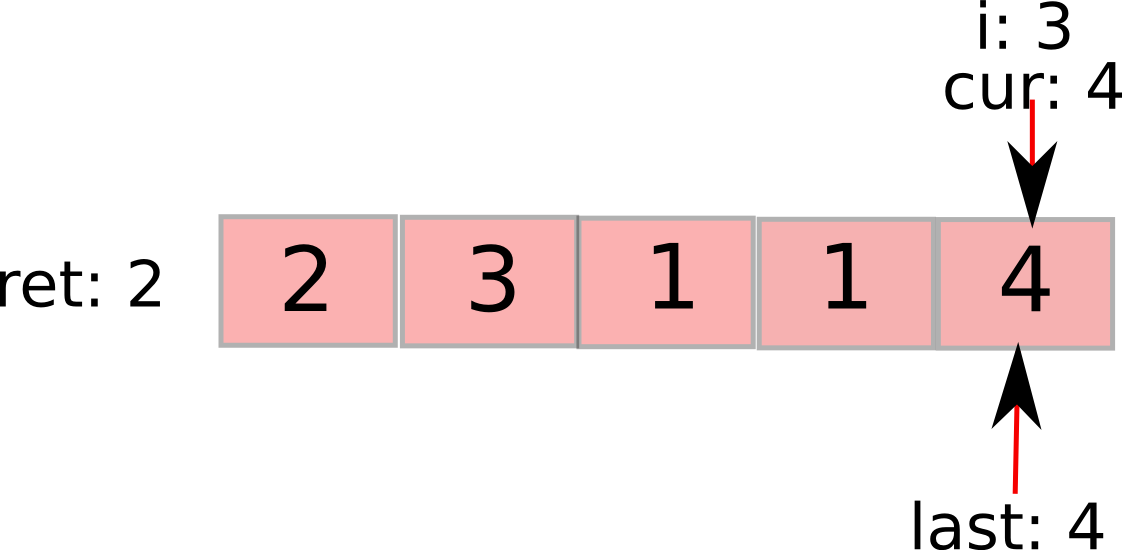
这道题让我们明白一个道理:
不要做无必要的计算。
对了,有同学会问,那为啥要用last,直接用curr跳不就行了。直接用curr跳那每次都是跳最远的,但是最优路径不不一定是这样。该算法时间复杂度为O(n)。
数组中的元素值是代表一个范围区间,题目需要求的是最小跳跃次数,也就是每一次的跳跃覆盖的范围应该尽可能远,这是一个大致思路。
- 假设 [ start, end ] 表示第 i 次跳跃才能到达的区间,nextEnd 代表在该区间中起跳的下一个最远元素,那么,[ end+1, nextEnd ] 表示第 i+1 次跳才能去到的范围区间。
- 初始化 [start , end] 为 [0,0],重复执行上面操作,直到 [start, end] 覆盖到终点元素。由于 [start, end] 表示第 i 次跳跃才能到达的区间,所以 i 便是最小的跳跃次数。
在代码实现中, start 变量没有影响到程序的执行,加进去只是为了方便理解。
1 int jump(vector<int>& nums) { 2 3 int start = 0; 4 int end = 0; 5 6 int cnt = 0; 7 8 int nextEnd = 0; 9 10 for (int i = 0 ; i < nums.size()-1; i++) { 11 12 if (i > end) { 13 return -1; 14 } 15 16 nextEnd = max(nextEnd, i + nums[i]); 17 if (i == end) { 18 start = i + 1; 19 end = nextEnd; 20 cnt++; 21 } 22 } 23 24 return cnt; 25 }
https://leetcode.com/problems/jump-game-ii/discuss/18019/10-lines-C%2B%2B-(16ms)-Python-BFS-Solutions-with-Explanations
This problem has a nice BFS structure. Let's illustrate it using the example
nums = [2, 3, 1, 1, 4] in the problem statement. We are initially at position 0. Then we can move at most nums[0] steps from it. So, after one move, we may reach nums[1] = 3 or nums[2] = 1. So these nodes are reachable in 1 move. From these nodes, we can further move to nums[3] = 1 and nums[4] = 4. Now you can see that the target nums[4] = 4 is reachable in 2 moves.
Putting these into codes, we keep two pointers
start and end that record the current range of the starting nodes. Each time after we make a move, update start to be end + 1 and end to be the farthest index that can be reached in 1 move from the current [start, end].
To get an accepted solution, it is important to handle all the edge cases. And the following codes handle all of them in a unified way without using the unclean
https://leetcode.com/problems/jump-game-ii/discuss/18014/Concise-O(n)-one-loop-JAVA-solution-based-on-Greedyif statements
The main idea is based on greedy. Let's say the range of the current jump is [curBegin, curEnd], curFarthest is the farthest point that all points in [curBegin, curEnd] can reach. Once the current point reaches curEnd, then trigger another jump, and set the new curEnd with curFarthest, then keep the above steps, as the following:
public int jump(int[] A) {
int jumps = 0, curEnd = 0, curFarthest = 0;
for (int i = 0; i < A.length - 1; i++) {
curFarthest = Math.max(curFarthest, i + A[i]);
if (i == curEnd) {
jumps++;
curEnd = curFarthest;
}
}
return jumps;
}
public int jump(int[] A) {
if (A == null || A.length == 0) {
return -1;
}
int start = 0, end = 0, jumps = 0;
while (end < A.length - 1) {
jumps++;
int farthest = end;
for (int i = start; i <= end; i++) {
if (A[i] + i > farthest) {
farthest = A[i] + i;
}
}
start = end + 1;
end = farthest;
}
return jumps;
}
https://leetcode.com/problems/jump-game-ii/discuss/18028/O(n)-BFS-solutionI try to change this problem to a BFS problem, where nodes in level i are all the nodes that can be reached in i-1th jump. for example. 2 3 1 1 4 , is
2||
3 1||
1 4 ||
3 1||
1 4 ||
clearly, the minimum jump of 4 is 2 since 4 is in level 3. my ac code.
Just to make it clear, this is a greedy solution inspired by BFS, not standard BFS whose time complexity should be O(N^2).
int jump(int A[], int n) {
if(n<2)return 0;
int level=0,currentMax=0,i=0,nextMax=0;
while(currentMax-i+1>0){ //nodes count of current level>0
level++;
for(;i<=currentMax;i++){ //traverse current level , and update the max reach of next level
nextMax=max(nextMax,A[i]+i);
if(nextMax>=n-1)return level; // if last element is in level+1, then the min jump=level
}
currentMax=nextMax;
}
return 0;
}http://fisherlei.blogspot.com/2012/12/leetcode-jump-ii.html
二指针问题,最大覆盖区间。
从左往右扫描,维护一个覆盖区间,每扫过一个元素,就重新计算覆盖区间的边界。比如,开始时区间[start, end], 遍历A数组的过程中,不断计算A[i]+i最大值(即从i坐标开始最大的覆盖坐标),并设置这个最大覆盖坐标为新的end边界。而新的start边界则为原end+1。不断循环,直到end> n.
1: int jump(int A[], int n) {
2: // Start typing your C/C++ solution below
3: // DO NOT write int main() function
4: int start = 0;
5: int end = 0;
6: int count =0;
7: if(n == 1) return 0;
8: while(end < n)
9: {
10: int max = 0;
11: count++;
12: for(int i =start; i<= end ; i++ )
13: {
14: if(A[i]+i >= n-1)
15: {
16: return count;
17: }
18: if(A[i]+ i > max)
19: max = A[i]+i;
20: }
21: start = end+1;
22: end = max;
23: }
24: }
维护l,r为当前的区间(类似BFS的思想),然后每次在这区间中取能跳到的最远距离,这区间的step都是相同的。
若最终r比n-1大,说明可以到达,且step步。复杂度也是O(n)
int jump(vector<int>& nums) {
int n = nums.size();
int l = 0, r = 0, step = 0;
while(r < n - 1){
int nr = r;
for(int i = l; i <= r; ++i)
nr = max(nr, i + nums[i]);
++step;
l = r + 1;
r = nr;
}
return step;
}
https://leetcode.com/problems/jump-game-ii/discuss/18152/Java-Solution-with-explanationpublic int jump(int[] nums) {
// If nums.length < 2, means that we do not
// need to move at all.
if (nums == null || nums.length < 2) {
return 0;
}
// First set up current region, which is
// from 0 to nums[0].
int l = 0;
int r = nums[0];
// Since the length of nums is greater than
// 1, we need at least 1 step.
int step = 1;
// We go through all elements in the region.
while (l <= r) {
// If the right of current region is greater
// than nums.length - 1, that means we are done.
if (r >= nums.length - 1) {
return step;
}
// We should know how far can we reach in current
// region.
int max = Integer.MIN_VALUE;
for (; l <= r; l++) {
max = Math.max(max, l + nums[l]);
}
// If we can reach far more in this round, we update
// the boundary of current region, and also add a step.
if (max > r) {
l = r;
r = max;
step++;
}
}
// We can not finish the job.
return -1;
}
This problem has a nice BFS structure. Let's illustrate it using the example nums = [2, 3, 1, 1, 4] in the problem statement. We are initially at position 0. Then we can move at most nums[0] steps from it. So, after one move, we may reach nums[1] = 3 or nums[2] = 1. So these nodes are reachable in 1 move. From these nodes, we can further move to nums[3] = 1 and nums[4] = 4. Now you can see that the target nums[4] = 4 is reachable in 2 moves.
Putting these into codes, we keep two pointers start and end that record the current range of the starting nodes. Each time after we make a move, update start to be end + 1 and end to be the farthest index that can be reached in 1 move from the current [start, end].
- time O(N)
- space O(1)
class Solution:
def jump(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
n = len(nums)
if n < 2:
return 0
step = 0
left = right = maxend = 0
while True: # we'll reach the end anyways, as stated
step += 1
for i in range(left, right+1): # make sure to include current start
if i + nums[i] >= n-1:
return step
maxend = max(maxend, i + nums[i])
left, right = right+ 1, maxend
public int jump(int[] nums) {
boolean[] visited = new boolean[nums.length];
Queue<Integer> q = new LinkedList<>();
q.add(0);
visited[0] = true;
int depth = 0;
while(!q.isEmpty())
{
int size = q.size();
for(int i=0; i<size; i++)
{
int index = q.remove();
if(index==nums.length-1) return depth;
for(int j=1; j<=nums[index]; j++)
{
int neighbor_index = index + j;
//if(neighbor_index==nums.length-1) return depth+1;
if(neighbor_index>nums.length-1) break;
if(visited[neighbor_index]) continue;
q.add(neighbor_index);
visited[neighbor_index]=true;
}
}
depth++;
}
return -1;
}X. DP
https://www.jiuzhang.com/solution/jump-game-ii/
// version 1: Dynamic Programming
// 这个方法,复杂度是 O(n^2),会超时,但是依然需要掌握。
public int jump(int[] A) {
// state
int[] steps = new int[A.length];
// initialize
steps[0] = 0;
for (int i = 1; i < A.length; i++) {
steps[i] = Integer.MAX_VALUE;
}
// function
for (int i = 1; i < A.length; i++) {
for (int j = 0; j < i; j++) {
if (steps[j] != Integer.MAX_VALUE && j + A[j] >= i) {
steps[i] = Math.min(steps[i], steps[j] + 1);
}
}
}
// answer
return steps[A.length - 1];
}
}
解题思路:dp递推,从当前下标能抵达的最远下标开始往前更新步数,步数更新为当前的最少步数+1。
int jump(vector<int>& nums) {
int n = nums.size();
if(n == 0 )
return 0;
int dp[n];
int inf = (1 << 31) - 1;
dp[0] = 0;
for(int i = 1;i < n; i++){
dp[i] = inf;
}
for(int i = 0;i < n; i++){
int j = min(i + nums[i],n-1);
for(;j >= i;j--){
if(dp[j] < inf)
break;
dp[j] = min(dp[i] + 1,dp[j]);
}
}
return dp[n-1];
}
1 public static int jump(int[] A) { 2 // Start typing your Java solution below 3 // DO NOT write main() function 4 if(A.length < 2) return 0; 5 int[] dist = new int[A.length]; 6 int[] to = new int[A.length]; 7 for(int i = 0; i < A.length; i++){ 8 dist[i] = INFINITE; 9 } 10 dist[A.length - 1] = 0; 11 for(int i = A.length - 2; i >= 0; i--){ 12 int minDist = INFINITE; 13 for(int j = 1; j <= A[i] && i + j < A.length; j++){ 14 int nextIdx = i + j; 15 if(nextIdx < A.length){ 16 int candidate = dist[nextIdx] + 1; 17 if(candidate < minDist){ 18 minDist = candidate; 19 to[i] = nextIdx; 20 } 21 } 22 } 23 dist[i] = minDist; 24 } 25 return dist[0]; 26 }
Trying to find a recursive solution
The first thing I try to do is find a recursive solution. Suppose I am trying to write a function, $minJumps(index)$, which will return me the minimum number of jumps to get from $index$ to the end of the array (so $minJumps(0)$ would be the solution to the problem).
Let’s call the last index, $n$. Then, we have the base case that $minJumps(n) = 0$. Now, when trying to write $minJumps(k)$ for an arbitrary $k$, we can apply the recursive assumption and imagine that $minJumps(index)$ would correctly return the minimum number of jumps for any index from $k+1$ to $n$. Then, we can get the correct answer for $minJumps(k)$ by simply trying each index that we can jump to. In mathematical terms:
Analyzing the recursive solution’s complexity
What kind of complexity does this lead to?
We can imagine that the code for the recursive case would be a for loop running over indices from $k+1$ to $k+A[k]$ and making a recursive call at each index. In the worst case, let’s imagine that $A[k] = n$. Then, we can see that the running time at index $k$ would be:
I don’t know the exact complexity of this, but I can tell you that it’s at least exponential (given that if it were only the first two terms in the sum it would be the same as fibonacci). Much like fibonacci, we should be able to make this much better by computing it with dynamic programming.
Applying dynamic programming
Let’s imagine that we computed each recursive call from the end of the array back to the beginning and stored the result (in an auxiliary array) so that each recursive call would return in constant time. Would this reduce the overall complexity?
If we do that, our running time would be (similar to insertion sort): $\sum_{i=1}^{n}i = O(n^2)$
Certainly better than exponential, but can we do even better?
Imagining the computation, I don’t see an easy way to reduce the amount of work done.
Trying to get a recursive solution from the other direction.
Let’s try defining $minSteps(i)$ as the minimum number of steps to start at index $0$ and reach index, $i$ (the opposite of what we did before). Assume we are writing $minSteps(i)$ and then use the recursive assumption to say that $minSteps(k)$ works for all $k < i$. How do we get an answer for $minSteps(i)$?
Let’s consider each previous index, (indices from $0$ to $i-1$), and find the ones that allow us to reach index $i$, then take the best one. Mathematically: .
Let’s suppose we compute this solution using dynamic programming, what would the complexity be? For each $i$, we have to check all previous indices, so our complexity is $T(n) = \sum_{i=1}^{n}i = O(n^2)$ again.
No better than the other way.
Trying to eliminate some repeated work
Imagining how the computation for the dynamic program would proceed, I can see some repeated work. When we compute the answer for an index, $k$, we’re redoing the entire min calculation just to see which indices apply to index $k$ but not index $k-1$. Can we eliminate some of that work?

Also, if we think about it, we’ll end up filling the ‘cost’ array and it will look something like:
| 0,1,1,…,1,2,2,…,2,3,3,…,3,…,?,?,?,? |
Maybe we can directly compute the index where we change from 0 to 1, 1 to 2, etc., i.e. find the largest index we can reach for a given number of steps?
Let’s try repeatedly computing the highest index we can reach for a given number of steps. Once that index is $>= n$, we know the minimum number of steps required (the solution).
When computing this, if we know the last 2 farthest indices, farthest index we can process in $k-1$ steps and the farthest index we can process in $k-2$ steps, we only need to check
Mathematically:
The complexity of this solution should be just $O(n)$ because we only have to look at each index in the array once.
Coding the solution
Before we code the solution, let’s draw a diagram showing what we are planning to do:

Then, we can write our code (in python3 and with leetcode boilerplate):
class Solution(object):
def jump(self, nums):
farthest_reachable = 0
num_steps = 0
next_index = 0
while (farthest_reachable < (len(nums) - 1)):
new_farthest_index = farthest_reachable;
while (next_index <= farthest_reachable and farthest_reachable < len(nums)):
new_farthest_index = max(new_farthest_index, next_index + nums[next_index])
next_index += 1
num_steps += 1
farthest_reachable = new_farthest_index
return num_steps
This could actually be done with a single loop, but I find it easy to understand the code this way.
Before ‘submitting’ this code, I think of a loop invariant, not necessarily formally, for my loops. The first loop’s purpose is to update ‘farthest_reachable’. At the start and end of it, I should check that ‘farthest_reachable’ is the farthest index that can be reached in ‘num_steps’ and that ‘next_index’ points to the first index that isn’t processed. I personally don’t bother with the inner loop’s loop invariant, but you could also reason about that if you wanted.