https://leetcode.com/problems/generate-random-point-in-a-circle/
X.
http://www.cnblogs.com/grandyang/p/9741220.html
这道题给了我们一个圆,包括中点位置和半径,让我们随机生成圆中的任意一个点。这里说明了圆上也当作是圆中,而且这里的随机意味着要等概率。思绪飘回了高中时代,努力搜索着那一丝丝残留的记忆,终于,我把还给老师的知识又要了回来,圆的方程表示为 (x - a) ^ 2 + (y - b) ^ 2 = r ^ 2,这里的 (a, b) 是圆心位置,r为半径。那么我们想如何生成圆中的任意位置呢,如果用这种方式来生成,那么我们先随机出一个x,那么随机出y的时候还要考虑其是否在圆中间,比较麻烦。继续回到高中时代,模糊的记忆中飘来了三个字,极坐标。是的,圆还可以用极坐标的形式来表示,我们只需随机出一个角度theta,再随机出一个小于半径的长度,这样我们就可以得到圆中的坐标位置了,哦耶~ 那么先来生成theta吧,我们知道一圈是360度,即2pi,所以我们随机出一个 [0, 1] 中的小数,再乘以2pi,就可以了。然后就是随机小于半径的长度,这里有个问题需要注意一下,我们并不是直接随机出一个 [0, 1] 中的小数再乘以半径r,而是要对随机出的[0, 1] 中的小数取个平方根再乘以半径r。这是为啥呢,简单来说,是为了保证等概率。如果不用平方根的话,那么表示圆的时候 (len * cos(theta)) ^ 2 + (len * sin(theta) ^ 2,这里就相当于对随机出的[0, 1] 中的小数平方了,那么其就不是等概率的了,因为两个小于1的小数相乘了,其会更加靠近0,这就是为啥我们要平方一下的原因。最后在求点位置的时候要加上圆心的偏移即可
直接对角度和半径都进行随机取样会产生这样的后果,靠近圆心的点被选择的概率偏大(Uniform random points in a circle using polar coordinates):
 https://leetcode.com/problems/generate-random-point-in-a-circle/discuss/154037/Polar-Coordinates-10-lines
https://leetcode.com/problems/generate-random-point-in-a-circle/discuss/154037/Polar-Coordinates-10-lines
X.
http://www.cnblogs.com/grandyang/p/9741220.html
我们也可以不用极坐标来做,由于之前刚做过Implement Rand10() Using Rand7(),对其中的拒绝采样Rejection Sampling还有印象,所以我们也可以用其来做。这其实就是拒绝采样的经典应用,在一个正方形中有均匀分布的点,让我们随机出其内切圆中的一个点,那么就是我们随机出x和y之后,然后算其平方和,如果小于等于r平方,说明其在圆内,我们可以返回其坐标,记得加上圆心偏移,否则我们重新进行采样。关于拒绝采样的方法可以参见我之前那篇博客Implement Rand10() Using Rand7()
https://zhanghuimeng.github.io/post/leetcode-478-generate-random-point-in-a-circle/
https://leetcode.com/problems/generate-random-point-in-a-circle/discuss/154027/Straight-forward-Java-AC-solution
https://leetcode.com/problems/generate-random-point-in-a-circle/discuss/154092/Very-simple-Python-solution
https://leetcode.com/problems/generate-random-point-in-a-circle/discuss/162295/How-is-the-solution-verified
https://leetcode.com/problems/generate-random-point-in-a-circle/discuss/155650/Explanation-with-Graphs-why-using-Math.sqrt()
Given the radius and x-y positions of the center of a circle, write a function
randPoint which generates a uniform random point in the circle.
Note:
- input and output values are in floating-point.
- radius and x-y position of the center of the circle is passed into the class constructor.
- a point on the circumference of the circle is considered to be in the circle.
randPointreturns a size 2 array containing x-position and y-position of the random point, in that order.
Example 1:
Input: ["Solution","randPoint","randPoint","randPoint"] [[1,0,0],[],[],[]] Output: [null,[-0.72939,-0.65505],[-0.78502,-0.28626],[-0.83119,-0.19803]]
Example 2:
Input: ["Solution","randPoint","randPoint","randPoint"] [[10,5,-7.5],[],[],[]] Output: [null,[11.52438,-8.33273],[2.46992,-16.21705],[11.13430,-12.42337]]
Explanation of Input Syntax:
The input is two lists: the subroutines called and their arguments.
Solution's constructor has three arguments, the radius, x-position of the center, and y-position of the center of the circle. randPoint has no arguments. Arguments are always wrapped with a list, even if there aren't anyhttp://www.cnblogs.com/grandyang/p/9741220.html
这道题给了我们一个圆,包括中点位置和半径,让我们随机生成圆中的任意一个点。这里说明了圆上也当作是圆中,而且这里的随机意味着要等概率。思绪飘回了高中时代,努力搜索着那一丝丝残留的记忆,终于,我把还给老师的知识又要了回来,圆的方程表示为 (x - a) ^ 2 + (y - b) ^ 2 = r ^ 2,这里的 (a, b) 是圆心位置,r为半径。那么我们想如何生成圆中的任意位置呢,如果用这种方式来生成,那么我们先随机出一个x,那么随机出y的时候还要考虑其是否在圆中间,比较麻烦。继续回到高中时代,模糊的记忆中飘来了三个字,极坐标。是的,圆还可以用极坐标的形式来表示,我们只需随机出一个角度theta,再随机出一个小于半径的长度,这样我们就可以得到圆中的坐标位置了,哦耶~ 那么先来生成theta吧,我们知道一圈是360度,即2pi,所以我们随机出一个 [0, 1] 中的小数,再乘以2pi,就可以了。然后就是随机小于半径的长度,这里有个问题需要注意一下,我们并不是直接随机出一个 [0, 1] 中的小数再乘以半径r,而是要对随机出的[0, 1] 中的小数取个平方根再乘以半径r。这是为啥呢,简单来说,是为了保证等概率。如果不用平方根的话,那么表示圆的时候 (len * cos(theta)) ^ 2 + (len * sin(theta) ^ 2,这里就相当于对随机出的[0, 1] 中的小数平方了,那么其就不是等概率的了,因为两个小于1的小数相乘了,其会更加靠近0,这就是为啥我们要平方一下的原因。最后在求点位置的时候要加上圆心的偏移即可
坐标法
但是我觉得这个方法的逼格不够高。于是我心想,我们怎么表示一个圆内的点呢?那自然就是用极坐标法,半径+角度。那么我们随机一个半径,再随机一个角度,最后换算成直角坐标系里的坐标,不就可以了嘛!
……只是听上去可以而已……
交上去之后我发现,一共有8个测试样例,最后一个我总是过不去。我的随机性是不是真的写出了bug?我实在是想不出来错在哪里了,于是去看了看题解区——原来有这么多人和我有一样的困惑。是的,上述思路确实有问题。
当我写出上述代码的时候,我心里想的是:先用角度随机选择一条半径,然后在这条半径上随机选择一个点。但问题是我们不能把圆这样看成是很多半径的集合——或者说,这条半径上不同位置的点的密集程度是不一样的。显然距离圆心更远的一端被选择的概率应该更大
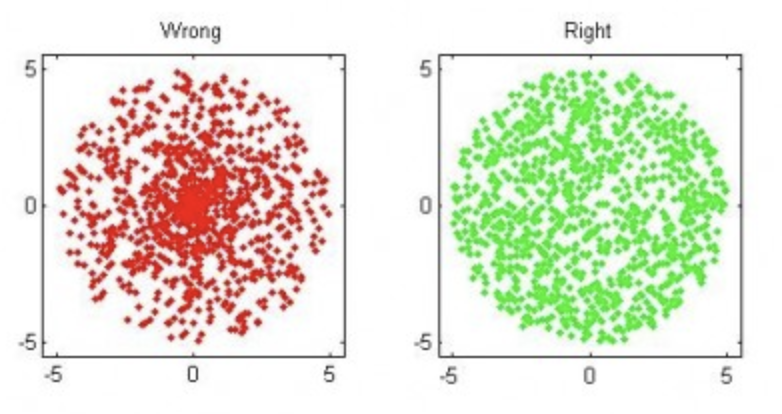
直接对角度和半径都进行随机取样会产生这样的后果,靠近圆心的点被选择的概率偏大(Uniform random points in a circle using polar coordinates):

右图这种对半径去根号的为什么是对的呢?因为我们产生的随机数是在0~1之间,那么去了根号之后会使得生成的点在1附近的密度更大,在0附近的密度变小。直觉上来看,那就是使得半径最外边被取到的概率变大,在圆心附近被取到的概率变小了。从而修正了圆心取到的点更密集的问题。
The point is that we should not use
x=rand(len)*cos(rand(degree)), we should use x=sqrt(rand(len))*cos(rand(degree)).
Reference: http://www.anderswallin.net/2009/05/uniform-random-points-in-a-circle-using-polar-coordinates/
double radius, x_center, y_center;
public Solution(double radius, double x_center, double y_center) {
this.radius=radius;
this.x_center=x_center;
this.y_center=y_center;
}
public double[] randPoint() {
double len= Math.sqrt(Math.random())*radius;
double deg= Math.random()*2*Math.PI;
double x= x_center+len*Math.cos(deg);
double y= y_center+len*Math.sin(deg);
return new double[]{x,y};
}
}
X.
http://www.cnblogs.com/grandyang/p/9741220.html
我们也可以不用极坐标来做,由于之前刚做过Implement Rand10() Using Rand7(),对其中的拒绝采样Rejection Sampling还有印象,所以我们也可以用其来做。这其实就是拒绝采样的经典应用,在一个正方形中有均匀分布的点,让我们随机出其内切圆中的一个点,那么就是我们随机出x和y之后,然后算其平方和,如果小于等于r平方,说明其在圆内,我们可以返回其坐标,记得加上圆心偏移,否则我们重新进行采样。关于拒绝采样的方法可以参见我之前那篇博客Implement Rand10() Using Rand7()
https://zhanghuimeng.github.io/post/leetcode-478-generate-random-point-in-a-circle/
拒绝取样
其实我的第一反应是用拒绝取样(Rejection Sampling)的思路来做:首先从这个圆的与坐标轴平行的外切正方形中均匀随机选取点,然后判断点是否位于圆中;如果不在,重新生成一个新的点,再次进行判断;否则直接返回。
https://leetcode.com/problems/generate-random-point-in-a-circle/discuss/154092/Very-simple-Python-solution
Since we are given the
(x, y) and r, so we can formulate this rectangle of [x-r, y-r, x+r, y+r]. It is very easy for us to make samples from squares uniformly, and we just reject the samples outside the circle. private double radius;
private double x_center;
private double y_center;
private double x_min;
private double y_min;
public Solution(double radius, double x_center, double y_center) {
this.radius = radius;
this.x_center = x_center;
this.y_center = y_center;
this.x_min = x_center - radius;
this.y_min = y_center - radius;
}
public double[] randPoint() {
while(true){
double randX = x_min + Math.random()*radius*2;
double randY = y_min + Math.random()*radius*2;
if(Math.pow(randX - x_center, 2) + Math.pow(randY - y_center, 2) <= radius * radius){
return new double[]{randX, randY};
}
}
}
https://leetcode.com/problems/generate-random-point-in-a-circle/discuss/155650/Explanation-with-Graphs-why-using-Math.sqrt()