http://www.cnblogs.com/grandyang/p/8993143.html
https://github.com/fishercoder1534/Leetcode/blob/master/src/main/java/com/fishercoder/solutions/_776.java
X.
Given a Binary Search Tree (BST) with root node
root, and a target value V, split the tree into two subtrees where one subtree has nodes that are all smaller or equal to the target value, while the other subtree has all nodes that are greater than the target value. It's not necessarily the case that the tree contains a node with value V.
Additionally, most of the structure of the original tree should remain. Formally, for any child C with parent P in the original tree, if they are both in the same subtree after the split, then node C should still have the parent P.
You should output the root TreeNode of both subtrees after splitting, in any order.
Example 1:
Input: root = [4,2,6,1,3,5,7], V = 2
Output: [[2,1],[4,3,6,null,null,5,7]]
Explanation:
Note that root, output[0], and output[1] are TreeNode objects, not arrays.
The given tree [4,2,6,1,3,5,7] is represented by the following diagram:
4
/ \
2 6
/ \ / \
1 3 5 7
while the diagrams for the outputs are:
4
/ \
3 6 and 2
/ \ /
5 7 1
Note:
- The size of the BST will not exceed
50. - The BST is always valid and each node's value is different.
通过观察我们首先发现,无论如何,root总是会包含在最终的返回结果中。然后就比较root的值和V的大小了:如果root的值比V大,那么root以及其右子树的结构都无需变化,只需要递归对root的左子树进行分割即可。需要注意的是,root的左子树中也有可能存在比V大的分支,所以我们需要将root的左子树中比V大的分支的树根接到root的左子树上。进一步分析可知,对root的左子树进行分割的思路和对root的分割完全一样,所以我们就可以采用递归调用进行处理了,代码十分简洁。
root的值小于等于V的情况可以对称得到处理。
root的值小于等于V的情况可以对称得到处理。
这道题给了我们一棵二叉搜索树Binary Search Tree,又给了我们一个目标值V,让我们将这个BST分割成两个子树,其中一个子树所有结点的值均小于等于目标值V,另一个子树所有结点的值均大于目标值V。这道题最大的难点在于不是简单的将某条边断开就可以的,不如题目中给的那个例子,目标值为2,我们知道要断开结点2和结点4的那条边,但是以结点2为root的子树中是有大于目标值2的结点的,而这个结点3必须也从该子树中移出,并加到较大的那个子树中去的。为了具体的讲解这个过程,这里借用官方解答贴中的例子来说明问题吧。

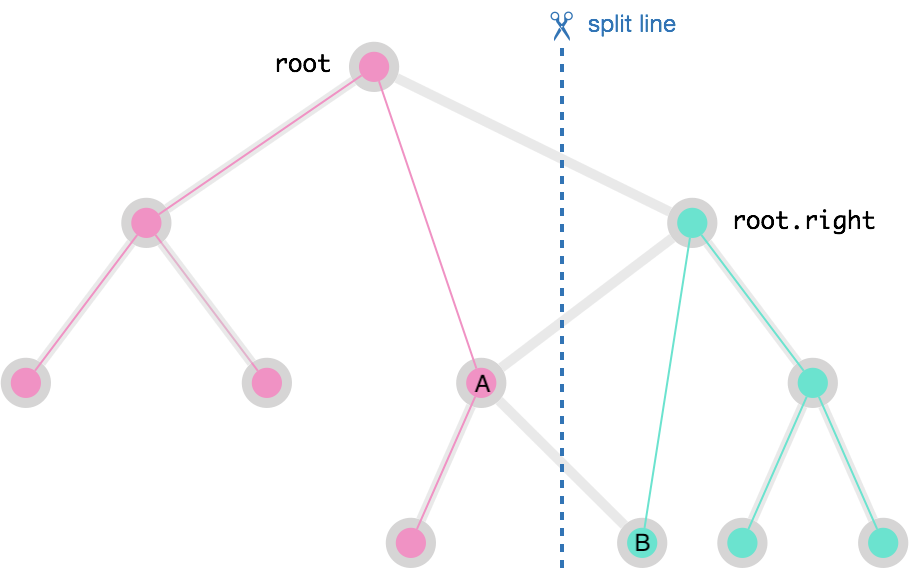
比如对于上图,假如root结点小于V,而root.right大于V的话,那么这条边是要断开的,但是如果root.right的左子结点(结点A)是小于V的,那么其边也应该断开,如果如果root.right的左子结点的右子结点(结点B)大于V,则这条边也应该断开,所以总共有三条边需要断开,如图中蓝色虚线所示,三条粗灰边需要断开,粉细边和绿细边是需要重新连上的边。那么我们应该如何知道连上哪条边呢?不要急,听博主慢慢道来。
博主告诉你们个秘密(一般人我不告诉他),对于树的题目,二话别说,直接上递归啊,除非是有啥特别要求,否则递归都可以解。而递归的精髓就是不断的DFS进入递归函数,直到递归到叶结点,然后回溯,我们递归函数的返回值是两个子树的根结点,比如对结点A调用递归,返回的第一个是A的左子结点,第二个是结点B,这个不需要重新连接,那么当回溯到root.right的时候,我们就需要让root.right结点连接上结点B,而这个结点B是对结点A调用递归的返回值中的第二个。如果是在左边,其实是对称的,root.left连接上调用递归返回值中的第一个,这两个想通了后,代码就不难写啦
vector<TreeNode*> splitBST(TreeNode* root, int V) { vector<TreeNode*> res{NULL, NULL}; if (!root) return res; if (root->val <= V) { res = splitBST(root->right, V); root->right = res[0]; res[0] = root; } else { res = splitBST(root->left, V); root->left = res[1]; res[1] = root; } return res; }
自底向下的遍历 O(h)h为树高度O(h)h为树高度
定义一个递归函数dfs,返回一个二维数组ans,当前结点和左右子树被V分割后,ans[0]为小于等于V的部分,ans[1]为大于V的部分。
如果当前结点node大于V,则ans[1]=node,对node的左子树递归调用dfs,得到当前结点左子树的分割结果(一个二维数组nodes)。当前结点的左子树设置为nodes[1],ans[0]设置为nodes[0]
如果当前结点node小于等于V,则ans[0]=node,对node的右子树递归调用dfs,得到当前结点右子树的分割结果(一个二维数组nodes)。当前结点的右子树设置为nodes[0],ans[1]设置为nodes[1]
时间复杂度分析:每次根据当前结点的值选择递归左子树或右子树,时间复杂度为树高度O(h)
public TreeNode[] splitBST(TreeNode root, int V) { if (root == null) return new TreeNode[]{null, null}; if (root.val == V) { TreeNode right = root.right; root.right = null; return new TreeNode[]{root, right}; } else if (root.val > V) { TreeNode[] nodes = splitBST(root.left, V); TreeNode left = nodes[0]; TreeNode right = nodes[1]; root.left = right; return new TreeNode[]{left,root}; } else { TreeNode[] nodes = splitBST(root.right, V); TreeNode left = nodes[0]; TreeNode right = nodes[1]; root.right=left; return new TreeNode[]{root, right}; } }
再来一种递归的思路,很简单。我们把问题进行拆分合并式求解。比如当root.val <= val时,说明root和root的左子树均小于等于val,这种结构维持,且以root为根,那么问题就转而求root右子树的分裂。因为分裂的第一颗树,是小于val的,所以需要链接到root的右子树上,详见代码。
public TreeNode[] splitBST(TreeNode root, int V) {
if (root == null)
return new TreeNode[] { null, null };
if (root.val <= V) {
TreeNode[] res = splitBST(root.right, V);
root.right = res[0];
res[0] = root;
return res;
} else {
TreeNode[] res = splitBST(root.left, V);
root.left = res[1];
res[1] = root;
return res;
}
}
https://github.com/fishercoder1534/Leetcode/blob/master/src/main/java/com/fishercoder/solutions/_776.java
public TreeNode[] splitBST(TreeNode root, int V) {
TreeNode small = new TreeNode(0);
TreeNode big = new TreeNode(0);
split(root, V, small, big);
return new TreeNode[] { small.right, big.left };
}
private void split(TreeNode root, int v, TreeNode small, TreeNode big) {
if (root == null) {
return;
}
if (root.val <= v) {
small.right = root;
TreeNode right = root.right;
root.right = null;
split(right, v, root, big);
} else {
big.left = root;
TreeNode left = root.left;
root.left = null;
split(left, v, small, root);
}
}
X.
问题的关键在于进行切分后,树的结构不能改变。影响BST的结构在于输入顺序,所以切分前后,维持输入顺序即可。而BST的层序遍历刚好是最初的输入顺序。所以
1. 求出输入顺序。
2. 根据val划分两个子输入顺序
3. 根据子输入顺序建立BST
1. 求出输入顺序。
2. 根据val划分两个子输入顺序
3. 根据子输入顺序建立BST
public TreeNode[] splitBST(TreeNode root, int V) {
if (root == null)
return new TreeNode[] { null, null };
List<Integer> nodes = new ArrayList<>();
Queue<TreeNode> q = new ArrayDeque<>();
q.offer(root);
while (!q.isEmpty()) {
TreeNode now = q.poll();
nodes.add(now.val);
if (now.left != null) {
q.offer(now.left);
}
if (now.right != null) {
q.offer(now.right);
}
}
List<Integer> left = new ArrayList<>();
List<Integer> right = new ArrayList<>();
for (int val : nodes) {
if (val <= V)
left.add(val);
else
right.add(val);
}
TreeNode leftNode = null;
for (int val : left)
leftNode = build(leftNode, val);
TreeNode rightNode = null;
for (int val : right)
rightNode = build(rightNode, val);
return new TreeNode[] { leftNode, rightNode };
}
TreeNode build(TreeNode root, int val) {
if (root == null)
return new TreeNode(val);
else {
if (val <= root.val) {
root.left = build(root.left, val);
} else {
root.right = build(root.right, val);
}
return root;
}
}