LeetCode 987 - Vertical Order Traversal of a Binary Tree

Related:LeetCode 314 - Binary Tree Vertical Order Traversal
https://leetcode.com/problems/vertical-order-traversal-of-a-binary-tree/

Given a binary tree, return the vertical order traversal of its nodes values.

For each node at position (X, Y), its left and right children respectively will be at positions (X-1, Y-1) and (X+1, Y-1).

Running a vertical line from X = -infinity to X = +infinity, whenever the vertical line touches some nodes, we report the values of the nodes in order from top to bottom (decreasing Y coordinates).

If two nodes have the same position, then the value of the node that is reported first is the value that is smaller.

Return an list of non-empty reports in order of X coordinate.  Every report will have a list of values of nodes.

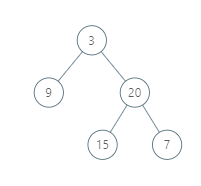
Example 1:

Input: [3,9,20,null,null,15,7]
Output: [[9],[3,15],[20],[7]]
Explanation: 
Without loss of generality, we can assume the root node is at position (0, 0):
Then, the node with value 9 occurs at position (-1, -1);
The nodes with values 3 and 15 occur at positions (0, 0) and (0, -2);
The node with value 20 occurs at position (1, -1);
The node with value 7 occurs at position (2, -2).

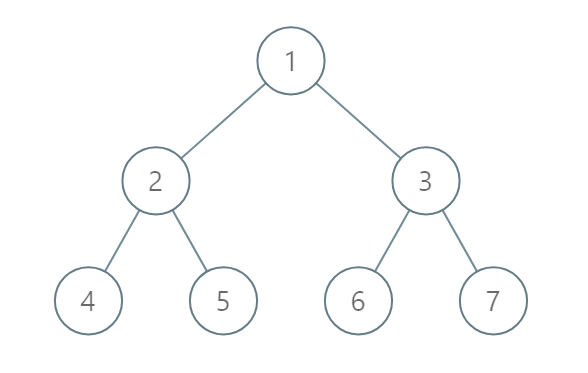
Example 2:

Input: [1,2,3,4,5,6,7]
Output: [[4],[2],[1,5,6],[3],[7]]
Explanation: 
The node with value 5 and the node with value 6 have the same position according to the given scheme.
However, in the report "[1,5,6]", the node value of 5 comes first since 5 is smaller than 6.

Note:

1. The tree will have between 1 and 1000 nodes.
2. Each node's value will be between 0 and 1000

When two nodes have the same position (i.e. same X and same Y value), 314 asks us to sort them in the result based on X ("from left to right"), while 987 asks us to sort them in the result based on the nodes' values.

X.
https://leetcode.com/problems/vertical-order-traversal-of-a-binary-tree/discuss/231125/Java-HashMap-and-TreeMap-and-PriorityQueue-Solution

1. we use a hashmap to record the x-coordinate of the nodes, and record the minX and maxX to get the values
2. we use a treemap to record the y-coordinate of the nodes, and use a priorityQueue to keep the ascending order

Possible Questions:

1. why use hashmap first then treemap？
   This is because hashmap can get the key in constant time, while treemap gets the key in O(logn) time, where n is the number of nodes. We need to traverse the hashmap from the smallest x to the highest x. And it is easy to realize that the value of x is always continuous. That is, the difference between two continugous x will only be 1. Thus, to traverse the hashmap, we just need to record the number of minimum x and maximum x.
   Unlike x, the value of y is not contiuous. And that's why we need a treemap. The function "keySet()" of treemap will return a series of keys in ascending order. And we can easily traverse the treemap by that.
2. Why use priorityQueue?
   Acutally it does not matter whether you use a priorityQueue or a List. The time complexity does not differ a lot. I think it is also a good idea to use ArrayList, and we need to sort it when we copy it to the final output.

    Map<Integer, TreeMap<Integer, PriorityQueue<Integer>>> map = new HashMap<>();
    int minX = 0, maxX = 0;
    public List<List<Integer>> verticalTraversal(TreeNode root) {
        helper(root, 0, 0);
        List<List<Integer>> vertical = new ArrayList<>();
        for (int i = minX; i <= maxX; i++) {
            List<Integer> level = new ArrayList<Integer>();
            for (int key : map.get(i).keySet()) {
                while (!(map.get(i).get(key)).isEmpty()) {
                    level.add(map.get(i).get(key).poll());
                }
            }
            vertical.add(level);
        }
        return vertical;
        
    }
    
    private void helper(TreeNode node, int x, int y) {
        if (node == null) return;
        minX = Math.min(minX, x);
        maxX = Math.max(maxX, x);
        if (map.get(x) == null) { map.put(x, new TreeMap<Integer, PriorityQueue<Integer>>()); }
        if (map.get(x).get(y) == null) { map.get(x).put(y, new PriorityQueue<Integer>()); }
        map.get(x).get(y).add(node.val);
        helper(node.left, x - 1, y + 1);
        helper(node.right, x + 1, y + 1);   

    }

https://leetcode.com/problems/vertical-order-traversal-of-a-binary-tree/discuss/231113/C%2B%2B-traverse-into-hashmapxy

Traverse the tree tracking x and y coordinates, and populate m[x][y] with values. Note that we use set to hold multiple values and sorts them automatically.

Then, we iterate x [-999, 999] and y [0, 999] and populate our answer. Since the tree size is limited to 1000, our coordinates will be within these intervals.

void traverse(TreeNode* r, int x, int y, unordered_map<int, unordered_map<int, set<int>>> &m) {
  if (r != nullptr) {
    m[x][y].insert(r->val);
    traverse(r->left, x - 1, y + 1, m);
    traverse(r->right, x + 1, y + 1, m);
  }
}
vector<vector<int>> verticalTraversal(TreeNode* r, vector<vector<int>> res = {}) {
  unordered_map<int, unordered_map<int, set<int>>> m;
  traverse(r, 0, 0, m);
  for (int x = -999; x < 1000; ++x) {
    if (m.find(x) != end(m)) {
      res.push_back(vector<int>());
      for (int y = 0; y < 1000; ++y)
        if (m[x].find(y) != end(m[x]))
          res.back().insert(end(res.back()), begin(m[x][y]), end(m[x][y]));
    }
  }
  return res;
}

X. TreeMap
https://leetcode.com/problems/vertical-order-traversal-of-a-binary-tree/discuss/231148/Java-TreeMap-Solution

    public List<List<Integer>> verticalTraversal(TreeNode root) {
        TreeMap<Integer, TreeMap<Integer, TreeSet<Integer>>> map = new TreeMap<>();
        dfs(root, 0, 0, map);
        List<List<Integer>> list = new ArrayList<>();
        for (TreeMap<Integer, TreeSet<Integer>> ys : map.values()) {
            list.add(new ArrayList<>());
            for (TreeSet<Integer> nodes : ys.values()) {
                for (int i : nodes) {
                    list.get(list.size() - 1).add(i);
                }
            }
        }
        return list;
    }
    private void dfs(TreeNode root, int x, int y, TreeMap<Integer, TreeMap<Integer, TreeSet<Integer>>> map) {
        if (root == null) {
            return;
        }
        if (!map.containsKey(x)) {
            map.put(x, new TreeMap<>());
        }
        if (!map.get(x).containsKey(y)) {
            map.get(x).put(y, new TreeSet<>());
        }
        map.get(x).get(y).add(root.val);
        dfs(root.left, x - 1, y + 1, map);
        dfs(root.right, x + 1, y + 1, map);
    }

https://zxi.mytechroad.com/blog/tree/leetcode-987-vertical-order-traversal-of-a-binary-tree/
Solution: Ordered Map+ Ordered Set
Time complexity: O(nlogn)
Space complexity: O(n)

  vector<vector<int>> verticalTraversal(TreeNode* root) {

    if (!root) return {};

    int min_x = INT_MAX;

    int max_x = INT_MIN;

    map<pair<int, int>, set<int>> h; // {y, x} -> {vals}

    traverse(root, 0, 0, h, min_x, max_x);

    vector<vector<int>> ans(max_x - min_x + 1);

    for (const auto& m : h) {      

      int x = m.first.second - min_x;

      ans[x].insert(end(ans[x]), begin(m.second), end(m.second));

    }

    return ans;

  }

private:

  void traverse(TreeNode* root, int x, int y,

                map<pair<int, int>, set<int>>& h,

                int& min_x,

                int& max_x) {

    if (!root) return;

    min_x = min(min_x, x);

    max_x = max(max_x, x);    

    h[{y, x}].insert(root->val);

    traverse(root->left, x - 1, y + 1, h, min_x, max_x);

    traverse(root->right, x + 1, y + 1, h, min_x, max_x);

  }

X. BFS, Level Order Traverse
https://leetcode.com/problems/vertical-order-traversal-of-a-binary-tree/discuss/231139/Java-HashMap-%2B-BFS

0. According to horizontal distance to build Map
1. In each horizontal distance, sort the node, first by vertical distance, then by val.

class Solution {
    class Node {
        TreeNode root;
        int hd;
        int vd;
        public Node(TreeNode root, int hd, int vd) {
            this.root = root;
            this.hd = hd;
            this.vd = vd;
        }
    }
    
    public List<List<Integer>> verticalTraversal(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        
        if (root == null) return res;
        Map<Integer, List<Node>> map = new HashMap<>();
        Queue<Node> q = new LinkedList<>();
        q.offer(new Node(root, 0, 0));
        int minHd = 0;
        int maxHd = 0;
        
        while (!q.isEmpty()) {
            Node cur = q.poll();
            map.putIfAbsent(cur.hd, new ArrayList<>());
            minHd = Math.min(minHd, cur.hd);
            maxHd = Math.max(maxHd, cur.hd);
            
            map.get(cur.hd).add(cur);
            if (cur.root.left != null) {
                q.offer(new Node(cur.root.left, cur.hd - 1, cur.vd - 1));
            }
            if (cur.root.right != null) {
                q.offer(new Node(cur.root.right, cur.hd + 1, cur.vd - 1));
            }
        }
        
        int index = 0;
        for (int i = minHd; i <= maxHd; i++) {

            Collections.sort(map.get(i), (a, b) -> {
                if (a.vd == b.vd) {
                    return a.root.val - b.root.val;
                } else {
                    return b.vd - a.vd;
                }
            });
            res.add(new ArrayList<>());
            for (Node node : map.get(i)) {
                res.get(index).add(node.root.val);
            }
            index++;
        }
        
        return res;
    }

X. https://leetcode.com/articles/vertical-order-traversal-of-a-binary-tree/
Approach 1: Store Locations

It's evident that there are two steps in a straightforward solution: first, find the location of every node, then report their locations.

Algorithm

To find the location of every node, we can use a depth-first search. During the search, we will maintain the location (x, y) of the node. As we move from parent to child, the location changes to (x-1, y+1) or (x+1, y+1) depending on if it is a left child or right child. [We use y+1 to make our sorting by decreasing y easier.]

To report the locations, we sort them by x coordinate, then y coordinate, so that they are in the correct order to be added to our answer.

• Time Complexity: $O(N \log N)$, where $N$ is the number of nodes in the given tree.
• Space Complexity: $O(N)$. 

  List<Location> locations;

  public List<List<Integer>> verticalTraversal(TreeNode root) {

    // Each location is a node's x position, y position, and value

    locations = new ArrayList();

    dfs(root, 0, 0);

    Collections.sort(locations);

    List<List<Integer>> ans = new ArrayList();

    ans.add(new ArrayList<Integer>());

    int prev = locations.get(0).x;

    for (Location loc : locations) {

      // If the x value changed, it's part of a new report.

      if (loc.x != prev) {

        prev = loc.x;

        ans.add(new ArrayList<Integer>());

      }

      // We always add the node's value to the latest report.

      ans.get(ans.size() - 1).add(loc.val);

    }

    return ans;

  }

  public void dfs(TreeNode node, int x, int y) {

    if (node != null) {

      locations.add(new Location(x, y, node.val));

      dfs(node.left, x - 1, y + 1);

      dfs(node.right, x + 1, y + 1);

    }

  }

}

class Location implements Comparable<Location> {

  int x, y, val;

  Location(int x, int y, int val) {

    this.x = x;

    this.y = y;

    this.val = val;

  }

  @Override

  public int compareTo(Location that) {

    if (this.x != that.x)

      return Integer.compare(this.x, that.x);

    else if (this.y != that.y)

      return Integer.compare(this.y, that.y);

    else

      return Integer.compare(this.val, that.val);

  }

https://leetcode.com/problems/vertical-order-traversal-of-a-binary-tree/discuss/231425/Java-Solution-using-Only-PriorityQueue

class Point{
    int x,y,val;
    Point(int x,int y,int val){
        this.x = x;
        this.y = y;
        this.val = val;
    }
}
public class Solution {
    public List<List<Integer>> verticalTraversal(TreeNode root) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        
        PriorityQueue<Point> pq = new PriorityQueue<Point>(1005,new Comparator<Point>(){
            public int compare(Point p1,Point p2){
                if(p1.x < p2.x) return -1;
                if(p2.x < p1.x) return 1;
                if(p1.y > p2.y) return -1;
                if(p1.y < p2.y) return 1;
                return p1.val - p2.val;
            }
        });
        
        verticalTraversalHelper(root,0,0,pq);
        Point prev = null;        
        List<Integer> l = new ArrayList<>();
        while(!pq.isEmpty()){
            Point p = pq.poll();
            if(prev == null || p.x != prev.x){
                if(prev != null) res.add(l);
                l = new ArrayList<>();
            }
            l.add(p.val);
            prev = p;
        }
        
        if(res.size() > 0) res.add(l);
        return res;
    }
    
    private void verticalTraversalHelper(TreeNode root,int x,int y,PriorityQueue<Point> pq){
        if(root == null) return;
        pq.offer(new Point(x,y,root.val));
        verticalTraversalHelper(root.left,x-1,y-1,pq);
        verticalTraversalHelper(root.right,x+1,y-1,pq);
    }
}