Related: LeetCode 505 - The Maze II
https://leetcode.com/articles/the-maze/
https://www.nowtoshare.com/zh/Article/Index/20455
X. DFS
Approach #1 Depth First Search [Time Limit Exceeded]
public boolean hasPath(int[][] maze, int[] start, int[] destination) { int m=maze.length; int n=maze[0].length; boolean[][] visited = new boolean[m][n]; visited[start[0]][start[1]]=true; return dfs(maze,visited,start,destination); } public boolean dfs(int[][] maze, boolean[][] visited, int[] pos , int[] dest ) { int[][] dirs = new int[][]{{-1,0},{1,0},{0,-1},{0,1}}; for(int[] dir : dirs) { int x=pos[0]+dir[0]; int y=pos[1]+dir[1]; while(x>=0 && x<maze.length && y>=0 && y<maze[0].length && maze[x][y]==0) { x+=dir[0]; y+=dir[1]; } x-=dir[0]; y-=dir[1]; if(dest[0]==x && dest[1]==y) return true; if(visited[x][y]) continue; visited[x][y]=true; boolean nextRound =dfs(maze,visited,new int[]{x,y},dest); if(nextRound) return true; } return false; }
https://discuss.leetcode.com/topic/77512/simple-java-dfs-with-comments
X. BFS
Approach #2 Breadth First Search [Accepted]
https://leetcode.com/articles/the-maze/
https://www.nowtoshare.com/zh/Article/Index/20455
There is a ball in a maze with empty spaces and walls. The ball can go through empty spaces by rolling up, down, left or right, but it won't stop rolling until hitting a wall. When the ball stops, it could choose the next direction.
Given the ball's start position, the destination and the maze, determine whether the ball could stop at the destination.
The maze is represented by a binary 2D array. 1 means the wall and 0 means the empty space. You may assume that the borders of the maze are all walls. The start and destination coordinates are represented by row and column indexes.
Example 1
Input 1: a maze represented by a 2D array 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 1 1 0 1 1 0 0 0 0 0 Input 2: start coordinate (rowStart, colStart) = (0, 4) Input 3: destination coordinate (rowDest, colDest) = (4, 4) Output: true Explanation: One possible way is : left -> down -> left -> down -> right -> down -> right.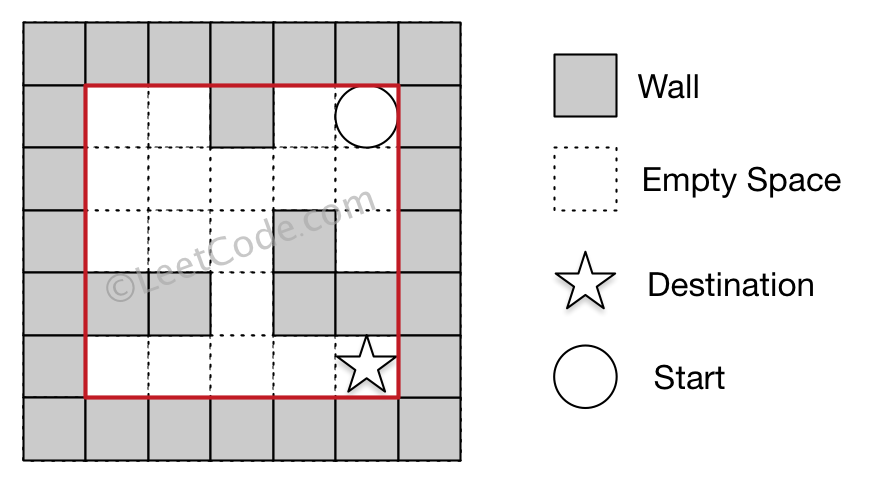
Example 2
Input 1: a maze represented by a 2D array 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 1 1 0 1 1 0 0 0 0 0 Input 2: start coordinate (rowStart, colStart) = (0, 4) Input 3: destination coordinate (rowDest, colDest) = (3, 2) Output: false Explanation: There is no way for the ball to stop at the destination.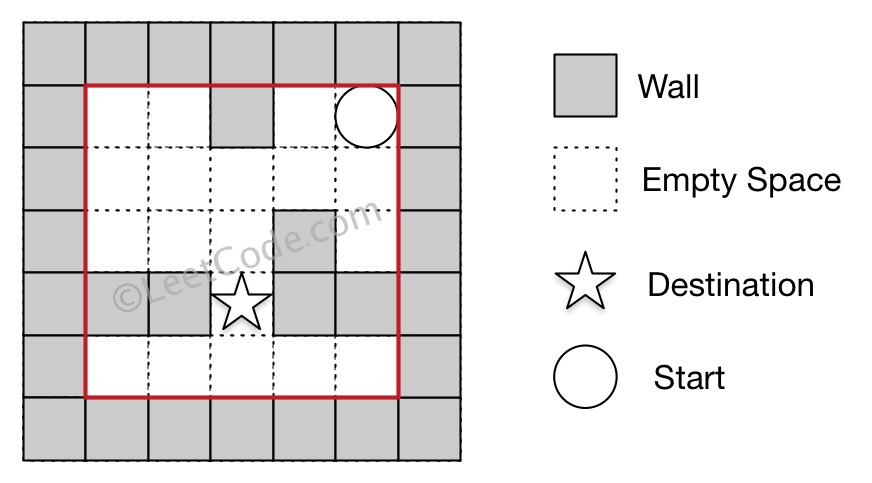
Note:
- There is only one ball and one destination in the maze.
- Both the ball and the destination exist on an empty space, and they will not be at the same position initially.
- The given maze does not contain border (like the red rectangle in the example pictures), but you could assume the border of the maze are all walls.
- The maze contains at least 2 empty spaces, and both the width and height of the maze won't exceed 100.
X. DFS
Approach #1 Depth First Search [Time Limit Exceeded]
public boolean hasPath(int[][] maze, int[] start, int[] destination) { int m=maze.length; int n=maze[0].length; boolean[][] visited = new boolean[m][n]; visited[start[0]][start[1]]=true; return dfs(maze,visited,start,destination); } public boolean dfs(int[][] maze, boolean[][] visited, int[] pos , int[] dest ) { int[][] dirs = new int[][]{{-1,0},{1,0},{0,-1},{0,1}}; for(int[] dir : dirs) { int x=pos[0]+dir[0]; int y=pos[1]+dir[1]; while(x>=0 && x<maze.length && y>=0 && y<maze[0].length && maze[x][y]==0) { x+=dir[0]; y+=dir[1]; } x-=dir[0]; y-=dir[1]; if(dest[0]==x && dest[1]==y) return true; if(visited[x][y]) continue; visited[x][y]=true; boolean nextRound =dfs(maze,visited,new int[]{x,y},dest); if(nextRound) return true; } return false; }
https://discuss.leetcode.com/topic/77512/simple-java-dfs-with-comments
- Search in the four possible directions when coming to a stopping point (i.e. a new starting point).
- Keep track of places that you already started at in case you roll back to that point.
private static final int[] DIRECTIONS = { 0, 1, 0, -1, 0 };
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
boolean[][] startedHere = new boolean[maze.length][maze[0].length];
return dfs(maze, startedHere, start, destination);
}
private boolean dfs(int[][] maze, boolean[][] startedHere, int[] start, int[] destination) {
if (startedHere[start[0]][start[1]]) return false;
if (Arrays.equals(start, destination)) return true;
startedHere[start[0]][start[1]] = true;
for (int i = 0; i < DIRECTIONS.length - 1; i++) {
int[] newStart = roll(maze, start[0], start[1], DIRECTIONS[i], DIRECTIONS[i + 1]);
if (dfs(maze, startedHere, newStart, destination)) return true;
}
return false;
}
private int[] roll(int[][] maze, int row, int col, int rowInc, int colInc) {
while (canRoll(maze, row + rowInc, col + colInc)) {
row += rowInc;
col += colInc;
}
return new int[]{row, col};
}
private boolean canRoll(int[][] maze, int row, int col) {
if (row >= maze.length || row < 0 || col >= maze[0].length || col < 0) return false;
return maze[row][col] != 1; // 1 is a wall
}
又是图的遍历问题,就是简单的遍历,所以dfs和bfs都可以做,复杂度也是一样的。这道题要求球不能停下来,即使碰到destination,必须是碰到wall才能停下来。
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
if(maze.length == 0 || maze[0].length == 0) return false;
if(start[0] == destination[0] && start[1] == destination[1]) return true;
m = maze.length; n = maze[0].length;
boolean[][] visited = new boolean[m][n];
return dfs(maze, start, destination, visited);
}
int m, n;
int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
private boolean dfs(int[][] maze, int[] cur, int[] dest, boolean[][] visited) {
// already visited
if(visited[cur[0]][cur[1]]) return false;
// reach destination
if(Arrays.equals(cur, dest)) return true;
visited[cur[0]][cur[1]] = true;
for(int[] dir : dirs) {
int nx = cur[0], ny = cur[1];
while(notWall(nx + dir[0], ny + dir[1]) && maze[nx+dir[0]][ny+dir[1]] != 1) {
nx += dir[0]; ny += dir[1];
}
if(dfs(maze, new int[] {nx, ny}, dest, visited)) return true;
}
return false;
}
private boolean notWall(int x, int y) {
return x >= 0 && x < m && y >= 0 && y < n;
}X. BFS
Approach #2 Breadth First Search [Accepted]
- Time complexity : . Complete traversal of maze will be done in the worst case. Here, and refers to the number of rows and coloumns of the maze.
- Space complexity : . array of size is used and size can grow upto in worst case.
class Point {
int x,y;
public Point(int _x, int _y) {x=_x;y=_y;}
}
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
int m=maze.length, n=maze[0].length;
if (start[0]==destination[0] && start[1]==destination[1]) return true;
int[][] dir=new int[][] {{-1,0},{0,1},{1,0},{0,-1}};
boolean[][] visited=new boolean[m][n];
LinkedList<Point> list=new LinkedList<>();
visited[start[0]][start[1]]=true;
list.offer(new Point(start[0], start[1]));
while (!list.isEmpty()) {
Point p=list.poll();
int x=p.x, y=p.y;
for (int i=0;i<4;i++) {
int xx=x, yy=y;
while (xx>=0 && xx<m && yy>=0 && yy<n && maze[xx][yy]==0) {
xx+=dir[i][0];
yy+=dir[i][1];
}
xx-=dir[i][0];
yy-=dir[i][1];
if (visited[xx][yy]) continue;
visited[xx][yy]=true;
if (xx==destination[0] && yy==destination[1]) return true;
list.offer(new Point(xx, yy));
}
}
return false;
} public boolean hasPath(int[][] maze, int[] start, int[] destination) {
int m = maze.length, n = maze[0].length;
boolean[][] visited = new boolean[m][n];
int[] dx = new int[]{0, -1, 0, 1};
int[] dy = new int[]{1, 0, -1, 0};
Queue<int[]> queue = new LinkedList<>();
queue.offer(start);
visited[start[0]][start[1]] = true;
while (!queue.isEmpty()) {
int[] curPos = queue.poll();
if (curPos[0] == destination[0] && curPos[1] == destination[1]) {
return true;
}
// try four direction until it hits the wall
for (int direction = 0; direction < 4; direction++) {
int nx = curPos[0], ny = curPos[1];
while (nx >= 0 && nx < m && ny >= 0 && ny < n && maze[nx][ny] == 0) {
nx += dx[direction];
ny += dy[direction];
}
//back one step
nx -= dx[direction];
ny -= dy[direction];
if (!visited[nx][ny]) {
visited[nx][ny] = true;
queue.offer(new int[]{nx, ny});
}
}
}
return false;
}