http://bookshadow.com/weblog/2017/05/07/leetcode-out-of-boundary-paths/
下面这种方法虽然也是用的DP解法,但是DP数组的定义和上面的不一样,这种解法相当于使用了BFS搜索,以(i, j)为起始点,其中dp[k][x][y]表示用了k步,进入(x, y)位置的路径数,由于dp[k][x][y]只依赖于dp[k-1][x][y],所以我们可以用一个二维dp数组来代替,初始化dp[i][j]为1,总共N步,进行N次循环,每次都新建一个mxn大小的临时数组t,然后就是对于遍历到的每个位置,都遍历其四个相邻位置,如果相邻位置越界了,那么我们用当前位置的dp值更新结果res,因为此时dp值的意义就是从(i,j)到越界位置的路径数。如果没有,我们将当前位置的dp值赋给t数组的对应位置,这样在遍历完所有的位置时,将数组t整个赋值给dp,然后进入下一步的循环
https://leetcode.com/problems/out-of-boundary-paths/discuss/102967/java-solution-dp-with-space-compression
由于结果可能是个巨大的数,所以让我们对一个大数取余。那么我们知道对于这种结果很大的数如果用递归解法很容易爆栈,所以最好考虑使用DP来解。那么我们使用一个三维的DP数组,其中dp[k][i][j]表示总共走k步,从(i,j)位置走出边界的总路径数。那么我们来找递推式,对于dp[k][i][j],走k步出边界的总路径数等于其周围四个位置的走k-1步出边界的总路径数之和,如果周围某个位置已经出边界了,那么就直接加上1,否则就在dp数组中找出该值,这样整个更新下来,我们就能得出每一个位置走任意步数的出界路径数了,最后只要返回dp[N][i][j]就是所求结果了
由于结果可能是个巨大的数,所以让我们对一个大数取余。那么我们知道对于这种结果很大的数如果用递归解法很容易爆栈,所以最好考虑使用DP来解。那么我们使用一个三维的DP数组,其中dp[k][i][j]表示总共走k步,从(i,j)位置走出边界的总路径数。那么我们来找递推式,对于dp[k][i][j],走k步出边界的总路径数等于其周围四个位置的走k-1步出边界的总路径数之和,如果周围某个位置已经出边界了,那么就直接加上1,否则就在dp数组中找出该值,这样整个更新下来,我们就能得出每一个位置走任意步数的出界路径数了,最后只要返回dp[N][i][j]就是所求结果了
http://imorrun.blogspot.com/2017/07/leetcode-576-out-of-boundary-paths.html
http://blog.csdn.net/anakin7/article/details/71787213
- How to make code clean
X. Approach #2 Recursion with memoization [Accepted]
X. BFS
https://buptwc.com/2018/07/19/Leetcode-576-Out-of-Boundary-Paths/
下面是bfs代码,在这道题中tle
https://leetcode.com/articles/out-of-boundary-paths/
Time complexity : . Size of recursion tree will be . Here, refers to the number of moves allowed.
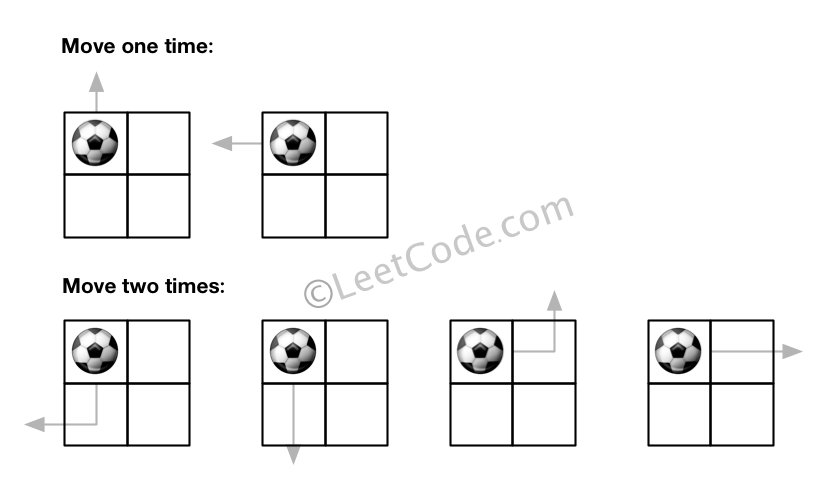
There is an m by n grid with a ball. Given the start coordinate (i,j) of the ball, you can move the ball to adjacent cell or cross the grid boundary in four directions (up, down, left, right). However, you can at most move N times. Find out the number of paths to move the ball out of grid boundary. The answer may be very large, return it after mod 109 + 7.
Example 1:
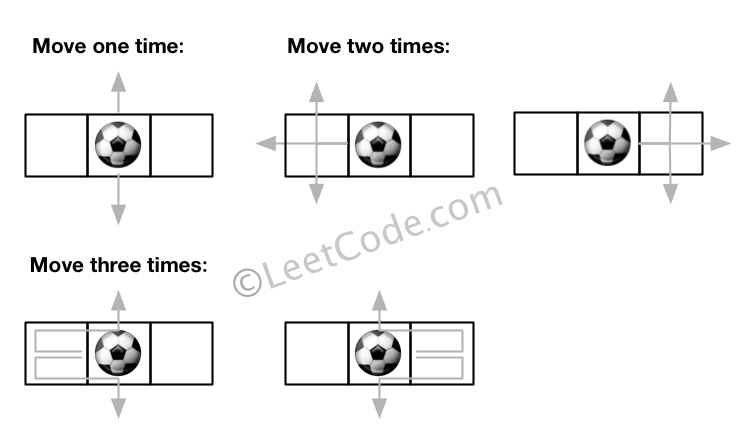
Example 2:
Note:
- Once you move the ball out of boundary, you cannot move it back.
- The length and height of the grid is in range [1,50].
- N is in range [0,50].
下面这种方法虽然也是用的DP解法,但是DP数组的定义和上面的不一样,这种解法相当于使用了BFS搜索,以(i, j)为起始点,其中dp[k][x][y]表示用了k步,进入(x, y)位置的路径数,由于dp[k][x][y]只依赖于dp[k-1][x][y],所以我们可以用一个二维dp数组来代替,初始化dp[i][j]为1,总共N步,进行N次循环,每次都新建一个mxn大小的临时数组t,然后就是对于遍历到的每个位置,都遍历其四个相邻位置,如果相邻位置越界了,那么我们用当前位置的dp值更新结果res,因为此时dp值的意义就是从(i,j)到越界位置的路径数。如果没有,我们将当前位置的dp值赋给t数组的对应位置,这样在遍历完所有的位置时,将数组t整个赋值给dp,然后进入下一步的循环
https://leetcode.com/problems/out-of-boundary-paths/discuss/102967/java-solution-dp-with-space-compression
DP[i][j][k] stands for how many possible ways to walk into cell j,k in step i, DP[i][j][k] only depends on DP[i - 1][j][k], so we can compress 3 dimensional dp array to 2 dimensional. public int findPaths(int m, int n, int N, int i, int j) {
if (N <= 0) return 0;
final int MOD = 1000000007;
int[][] count = new int[m][n];
count[i][j] = 1;
int result = 0;
int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
for (int step = 0; step < N; step++) {
int[][] temp = new int[m][n];
for (int r = 0; r < m; r++) {
for (int c = 0; c < n; c++) {
for (int[] d : dirs) {
int nr = r + d[0];
int nc = c + d[1];
if (nr < 0 || nr >= m || nc < 0 || nc >= n) {
result = (result + count[r][c]) % MOD;
}
else {
temp[nr][nc] = (temp[nr][nc] + count[r][c]) % MOD;
}
}
}
}
count = temp;
}
return result;
}
public int findPaths(int m, int n, int N, int x, int y) {
int M = 1000000000 + 7;
int dp[][] = new int[m][n];
dp[x][y] = 1;
int count = 0;
for (int moves = 1; moves <= N; moves++) {
int[][] temp = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (i == m - 1)
count = (count + dp[i][j]) % M;
if (j == n - 1)
count = (count + dp[i][j]) % M;
if (i == 0)
count = (count + dp[i][j]) % M;
if (j == 0)
count = (count + dp[i][j]) % M;
temp[i][j] = (((i > 0 ? dp[i - 1][j] : 0) + (i < m - 1 ? dp[i + 1][j] : 0)) % M
+ ((j > 0 ? dp[i][j - 1] : 0) + (j < n - 1 ? dp[i][j + 1] : 0)) % M) % M;
}
}
dp = temp;
}
return count;
}
http://www.cnblogs.com/grandyang/p/6927921.html由于结果可能是个巨大的数,所以让我们对一个大数取余。那么我们知道对于这种结果很大的数如果用递归解法很容易爆栈,所以最好考虑使用DP来解。那么我们使用一个三维的DP数组,其中dp[k][i][j]表示总共走k步,从(i,j)位置走出边界的总路径数。那么我们来找递推式,对于dp[k][i][j],走k步出边界的总路径数等于其周围四个位置的走k-1步出边界的总路径数之和,如果周围某个位置已经出边界了,那么就直接加上1,否则就在dp数组中找出该值,这样整个更新下来,我们就能得出每一个位置走任意步数的出界路径数了,最后只要返回dp[N][i][j]就是所求结果了
由于结果可能是个巨大的数,所以让我们对一个大数取余。那么我们知道对于这种结果很大的数如果用递归解法很容易爆栈,所以最好考虑使用DP来解。那么我们使用一个三维的DP数组,其中dp[k][i][j]表示总共走k步,从(i,j)位置走出边界的总路径数。那么我们来找递推式,对于dp[k][i][j],走k步出边界的总路径数等于其周围四个位置的走k-1步出边界的总路径数之和,如果周围某个位置已经出边界了,那么就直接加上1,否则就在dp数组中找出该值,这样整个更新下来,我们就能得出每一个位置走任意步数的出界路径数了,最后只要返回dp[N][i][j]就是所求结果了
int findPaths(int m, int n, int N, int i, int j) { vector<vector<vector<int>>> dp(N + 1, vector<vector<int>>(m, vector<int>(n, 0))); for (int k = 1; k <= N; ++k) { for (int x = 0; x < m; ++x) { for (int y = 0; y < n; ++y) { long long v1 = (x == 0) ? 1 : dp[k - 1][x - 1][y]; long long v2 = (x == m - 1) ? 1 : dp[k - 1][x + 1][y]; long long v3 = (y == 0) ? 1 : dp[k - 1][x][y - 1]; long long v4 = (y == n - 1) ? 1 : dp[k - 1][x][y + 1]; dp[k][x][y] = (v1 + v2 + v3 + v4) % 1000000007; } } } return dp[N][i][j]; }https://zxi.mytechroad.com/blog/dynamic-programming/leetcode-576-out-of-boundary-paths/
int findPaths(int m, int n, int N, int i, int j) {
constexpr int kMod = 1000000007;
vector<vector<int>> dp(m, vector<int>(n, 0));
vector<int> dirs{-1, 0, 1, 0, -1};
for (int s = 1; s <= N; ++s) {
vector<vector<int>> tmp(m, vector<int>(n, 0));
for (int y = 0; y < m; ++y)
for (int x = 0; x < n; ++x)
for (int d = 0; d < 4; ++d) {
int tx = x + dirs[d];
int ty = y + dirs[d + 1];
if (tx < 0 || ty < 0 || tx >= n || ty >= m)
tmp[y][x] += 1;
else
tmp[y][x] = (tmp[y][x] + dp[ty][tx]) % kMod;
}
dp.swap(tmp);
}
return dp[i][j];
}
class Solution(object):
def findPaths(self, m, n, N, i, j):
dp = [[0] * n for _ in range(m)]
for s in range(1, N + 1):
curStatus = [[0] * n for _ in range(m)]
for x in range(m):
for y in range(n):
v1 = 1 if x == 0 else dp[x - 1][y]
v2 = 1 if x == m - 1 else dp[x + 1][y]
v3 = 1 if y == 0 else dp[x][y - 1]
v4 = 1 if y == n - 1 else dp[x][y + 1]
curStatus[x][y] = (v1 + v2 + v3 + v4) % (10**9 + 7)
dp = curStatus
return dp[i][j]
Rolling Array:
int findPaths(int m, int n, int N, int i, int j) {
unsigned int dp[2][50][50] = {};
for (int x = 1; x <= N; ++x) {
for (int mi = 0; mi < m; ++mi) {
for (int ni = 0, nc = x % 2, np = (x - 1) % 2; ni < n; ++ni) {
dp[nc][mi][ni] = ((mi == 0 ? 1 : dp[np][mi - 1][ni]) +
(mi == m - 1 ? 1 : dp[np][mi + 1][ni]) +
(ni == 0 ? 1 : dp[np][mi][ni - 1]) +
(ni == n - 1 ? 1 : dp[np][mi][ni + 1])
) % 1000000007;
}
}
}
return N % 2 == 0 ? dp[0][i][j] : dp[1][i][j];
}
状态搜索
这个dp其实属于对状态的搜索,如果看了《计算机考研机试指南》或者《挑战程序设计竞赛》的话,会很清楚的知道其实这是个搜索的题目。归根到底都是对状态的转移问题,所以这个方法的名称叫做动归还是搜索都可以。
这种的做法有点类似于BFS搜索的题目,我们在做BFS的时候也会记录当前处于哪一步,所以是非常类似的。我们定义了四个搜索的方向,从当前位置向周围4个方向进行搜索,如果搜索到了边界以外,和上面的做法类似的,我们把当前的步数+1;如果在边界以内,那么就把当前第s步的结果增加第s-1步的(nx, ny)位置能到达边界的解法步数。
动态规划(Dynamic Programming)
数组dp[t][x][y]表示第t次移动时,坐标x, y处的移动路径总数。
状态转移方程:
当x + dx或者y + dy超出边界时,将结果累加至最终答案。
http://www.jianshu.com/p/5cd8eac78efb
一般矩阵题加了一个step的限制条件,则考虑用三维dp来做了。而递推公式如下(四个方向,step-1结果的和)
dp[i][j][step] = dp[i-1][j][step-1] + dp[i+1][j][step-1] + dp[i][j-1][step-1] + dp[i][j+1][step-1]
第一种解法:
https://discuss.leetcode.com/topic/88539/easy-understanding-c-python-solution-with-explanation
https://discuss.leetcode.com/topic/88539/easy-understanding-c-python-solution-with-explanation
思路直接,用dfs, 用中心向外正向搜索。如果对应的坐标+步数没被访问过,则以此继续向外dfs.
第二种方法是反向,由step1推到stepn, 由外向内收缩。在一步时,仅仅最外围的坐标可以获得值,而里层点都是0,因为里层点一步走不出去。二步,三步以此类推,均可由一步逆推出来。这种方法还可以用滚动数组节省空间。而值得注意的是一定要用uint或long,来防止overflow.
https://discuss.leetcode.com/topic/88492/c-6-lines-dp-o-n-m-n-6-ms
http://ying_xd.leanote.com/post/Leetcode-576-Out-of-Boundary-Paths
X.
下面这种方法虽然也是用的DP解法,但是DP数组的定义和上面的不一样,这种解法相当于使用了BFS搜索,以(i, j)为起始点,其中dp[k][x][y]表示用了k步,进入(x, y)位置的路径数,由于dp[k][x][y]只依赖于dp[k-1][x][y],所以我们可以用一个二维dp数组来代替,初始化dp[i][j]为1,总共N步,进行N次循环,每次都新建一个mxn大小的临时数组t,然后就是对于遍历到的每个位置,都遍历其四个相邻位置,如果相邻位置越界了,那么我们用当前位置的dp值更新结果res,因为此时dp值的意义就是从(i,j)到越界位置的路径数。如果没有,我们将当前位置的dp值赋给t数组的对应位置,这样在遍历完所有的位置时,将数组t整个赋值给dp,然后进入下一步的循环
http://blog.csdn.net/gqk289/article/details/73441022
其中当单元格 在越界时, 有
int findPaths(int m, int n, int N, int i, int j) {int dp[51][50][50] = {0};for (auto Ni = 1; Ni <= N; ++Ni)for (auto mi = 0; mi < m; ++mi)for (auto ni = 0; ni < n; ++ni) {dp[Ni][mi][ni] = ((long long)(mi == 0 ? 1 : dp[Ni - 1][mi - 1][ni]) +(mi == m - 1 ? 1 : dp[Ni - 1][mi + 1][ni]) +(ni == 0 ? 1 : dp[Ni - 1][mi][ni - 1]) +(ni == n - 1 ? 1 : dp[Ni - 1][mi][ni + 1])) % 1000000007;}return dp[N][i][j];}
http://ying_xd.leanote.com/post/Leetcode-576-Out-of-Boundary-Paths
X.
下面这种方法虽然也是用的DP解法,但是DP数组的定义和上面的不一样,这种解法相当于使用了BFS搜索,以(i, j)为起始点,其中dp[k][x][y]表示用了k步,进入(x, y)位置的路径数,由于dp[k][x][y]只依赖于dp[k-1][x][y],所以我们可以用一个二维dp数组来代替,初始化dp[i][j]为1,总共N步,进行N次循环,每次都新建一个mxn大小的临时数组t,然后就是对于遍历到的每个位置,都遍历其四个相邻位置,如果相邻位置越界了,那么我们用当前位置的dp值更新结果res,因为此时dp值的意义就是从(i,j)到越界位置的路径数。如果没有,我们将当前位置的dp值赋给t数组的对应位置,这样在遍历完所有的位置时,将数组t整个赋值给dp,然后进入下一步的循环
int findPaths(int m, int n, int N, int i, int j) { int res = 0; vector<vector<int>> dp(m, vector<int>(n, 0)); dp[i][j] = 1; vector<vector<int>> dirs{{0,-1},{-1,0},{0,1},{1,0}}; for (int k = 0; k < N; ++k) { vector<vector<int>> t(m, vector<int>(n, 0)); for (int r = 0; r < m; ++r) { for (int c = 0; c < n; ++c) { for (auto dir : dirs) { int x = r + dir[0], y = c + dir[1]; if (x < 0 || x >= m || y < 0 || y >= n) { res = (res + dp[r][c]) % 1000000007; } else { t[x][y] = (t[x][y] + dp[r][c]) % 1000000007; } } } } dp = t; } return res; }
http://imorrun.blogspot.com/2017/07/leetcode-576-out-of-boundary-paths.html
http://blog.csdn.net/anakin7/article/details/71787213
- How to make code clean
DP,时间复杂度O(m * n * step),dp[i][j]表示位置(i, j)的当前路径种数,内层循环每次初始化一个新的二维数组,用来记录当次遍历结果,遍历完之后赋值给cnt
- public int findPaths(int m, int n, int N, int a, int b) {
- if (N <= 0) {
- return 0;
- }
- int[][] cnt = new int[m][n];
- int res = 0;
- int mod = 1000000007;
- int[][] dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
- cnt[a][b] = 1;
- for (int i = 0; i < N; i++) {
- int[][] temp = new int[m][n];
- for (int j = 0; j < m; j++) {
- for (int k = 0; k < n; k++) {
- for (int[] dir : dirs) {
- int nm = j + dir[0];
- int nn = k + dir[1];
- if (nm < 0 || nn < 0 || nm >= m || nn >= n) {
- // 如果下一位置翻出去了,就只与前一次移动结果相关
- res = (res + cnt[j][k]) % mod;
- } else {
- temp[nm][nn] = (temp[nm][nn] + cnt[j][k]) % mod;
- }
- }
- }
- }
- cnt = temp;
- }
- return res;
- }
X. Approach #2 Recursion with memoization [Accepted]
- Time complexity : . We need to fill the array once with dimensions xx. Here, , refer to the number of rows and columns of the given grid respectively. refers to the total number of allowed moves.
- Space complexity : . array of size is used.
int M = 1000000007;
public int findPaths(int m, int n, int N, int i, int j) {
int[][][] memo = new int[m][n][N + 1];
for (int[][] l : memo)
for (int[] sl : l)
Arrays.fill(sl, -1);
return findPaths(m, n, N, i, j, memo);
}
public int findPaths(int m, int n, int N, int i, int j, int[][][] memo) {
if (i == m || j == n || i < 0 || j < 0)
return 1;
if (N == 0)
return 0;
if (memo[i][j][N] >= 0)
return memo[i][j][N];
memo[i][j][N] = ((findPaths(m, n, N - 1, i - 1, j, memo) + findPaths(m, n, N - 1, i + 1, j, memo)) % M
+ (findPaths(m, n, N - 1, i, j - 1, memo) + findPaths(m, n, N - 1, i, j + 1, memo)) % M) % M;
return memo[i][j][N];
}
X. BFS
https://buptwc.com/2018/07/19/Leetcode-576-Out-of-Boundary-Paths/
下面是bfs代码,在这道题中tle
def findPaths(m,n,N,i,j): mod = 10**9 + 7 Q = collections.deque([(i,j,0)]) res = 0 while Q: x,y,step = Q.popleft() if step > N: break if 0<=x<m and 0<=y<n: Q.append((x+1,y,step+1)) Q.append((x-1,y,step+1)) Q.append((x,y+1,step+1)) Q.append((x,y-1,step+1)) else: res += 1 return res % modX. Brute Force
https://leetcode.com/articles/out-of-boundary-paths/
In the brute force approach, we try to take one step in every direction and decrement the number of pending moves for each step taken. Whenever we reach out of the boundary while taking the steps, we deduce that one extra path is available to take the ball out.
In order to implement the same, we make use of a recursive function
findPaths(m,n,N,i,j) which takes the current number of moves() along with the current position( as some of the parameters and returns the number of moves possible to take the ball out with the current pending moves from the current position. Now, we take a step in every direction and update the corresponding indices involved along with the current number of pending moves.
Further, if we run out of moves at any moment, we return a 0 indicating that the current set of moves doesn't take the ball out of boundary.
public int findPaths(int m, int n, int N, int i, int j) {
if (i == m || j == n || i < 0 || j < 0)
return 1;
if (N == 0)
return 0;
return findPaths(m, n, N - 1, i - 1, j) + findPaths(m, n, N - 1, i + 1, j) + findPaths(m, n, N - 1, i, j - 1)
+ findPaths(m, n, N - 1, i, j + 1);
}