http://bookshadow.com/weblog/2017/05/15/leetcode-erect-the-fence/
public List<Point> outerTrees(Point[] points) { Point first = points[0]; int firstIndex = 0; // Find the leftmost point for (int i = 0; i < points.length; i++) { Point point = points[i]; if (point.x < first.x) { first = point; firstIndex = i; } } Set<Point> answer = new HashSet<>(); Point cur = first; int curIndex = firstIndex; answer.add(first); do { Point next = points[0]; int nextIndex = 0; for (int i = 1; i < points.length; i++) { if (i == curIndex) continue; Point p = points[i]; int cross = crossProductLength(p, cur, next); if (nextIndex == curIndex || cross > 0 || // Handle multi points in a line (cross == 0 && distance(p, cur) > distance(next, cur))) { next = p; nextIndex = i; } } // Handle multi points in a line for (int i = 0; i < points.length; i++) { Point p = points[i]; int cross = crossProductLength(p, cur, next); if (i != curIndex && cross == 0) { answer.add(p); } } cur = next; curIndex = nextIndex; } while (curIndex != firstIndex); return new ArrayList<>(answer); } private int crossProductLength(Point A, Point B, Point C) { // Get the vectors' coordinates. int BAx = A.x - B.x; int BAy = A.y - B.y; int BCx = C.x - B.x; int BCy = C.y - B.y; // Calculate the Z coordinate of the cross product. return (BAx * BCy - BAy * BCx); } private int distance(Point p1, Point p2) { return (p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y); }
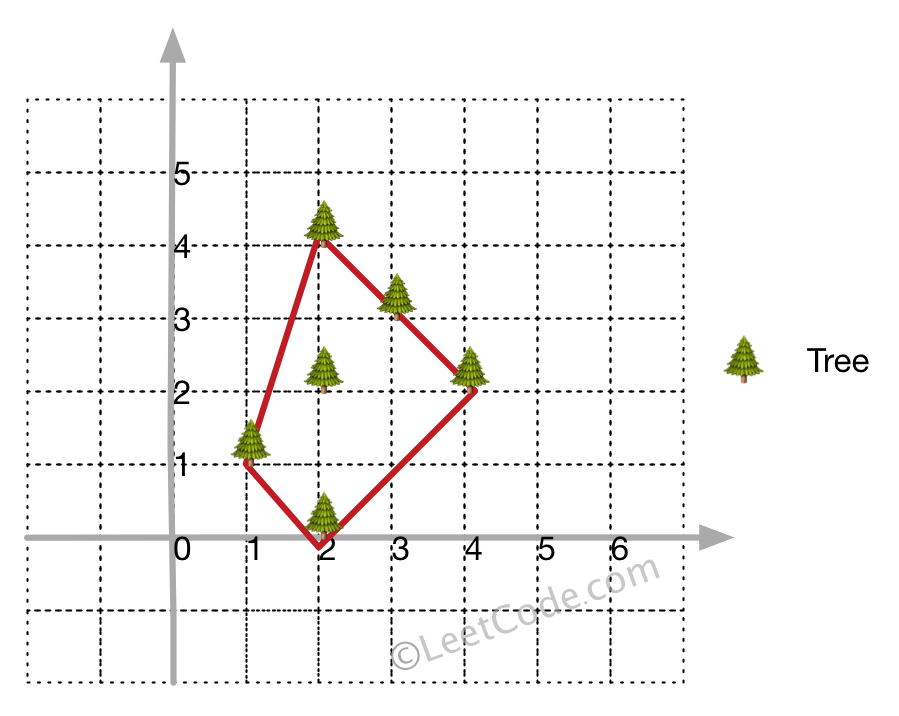
There are some trees, where each tree is represented by (x,y) coordinate in a two-dimensional garden. Your job is to fence the entire garden using the minimum length of rope as it is expensive. The garden is well fenced only if all the trees are enclosed. Your task is to help find the coordinates of trees which are exactly located on the fence perimeter.
Example 1:
Example 2:
Note:
- All trees should be enclosed together. You cannot cut the rope to enclose trees that will separate them in more than one group.
- All input integers will range from 0 to 100.
- The garden has at least one tree.
- All coordinates are distinct.
- Input points have NO order. No order required for output.
public List<Point> outerTrees(Point[] points) { Point first = points[0]; int firstIndex = 0; // Find the leftmost point for (int i = 0; i < points.length; i++) { Point point = points[i]; if (point.x < first.x) { first = point; firstIndex = i; } } Set<Point> answer = new HashSet<>(); Point cur = first; int curIndex = firstIndex; answer.add(first); do { Point next = points[0]; int nextIndex = 0; for (int i = 1; i < points.length; i++) { if (i == curIndex) continue; Point p = points[i]; int cross = crossProductLength(p, cur, next); if (nextIndex == curIndex || cross > 0 || // Handle multi points in a line (cross == 0 && distance(p, cur) > distance(next, cur))) { next = p; nextIndex = i; } } // Handle multi points in a line for (int i = 0; i < points.length; i++) { Point p = points[i]; int cross = crossProductLength(p, cur, next); if (i != curIndex && cross == 0) { answer.add(p); } } cur = next; curIndex = nextIndex; } while (curIndex != firstIndex); return new ArrayList<>(answer); } private int crossProductLength(Point A, Point B, Point C) { // Get the vectors' coordinates. int BAx = A.x - B.x; int BAy = A.y - B.y; int BCx = C.x - B.x; int BCy = C.y - B.y; // Calculate the Z coordinate of the cross product. return (BAx * BCy - BAy * BCx); } private int distance(Point p1, Point p2) { return (p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y); }
凸包(Convex Hull)
Graham扫描法
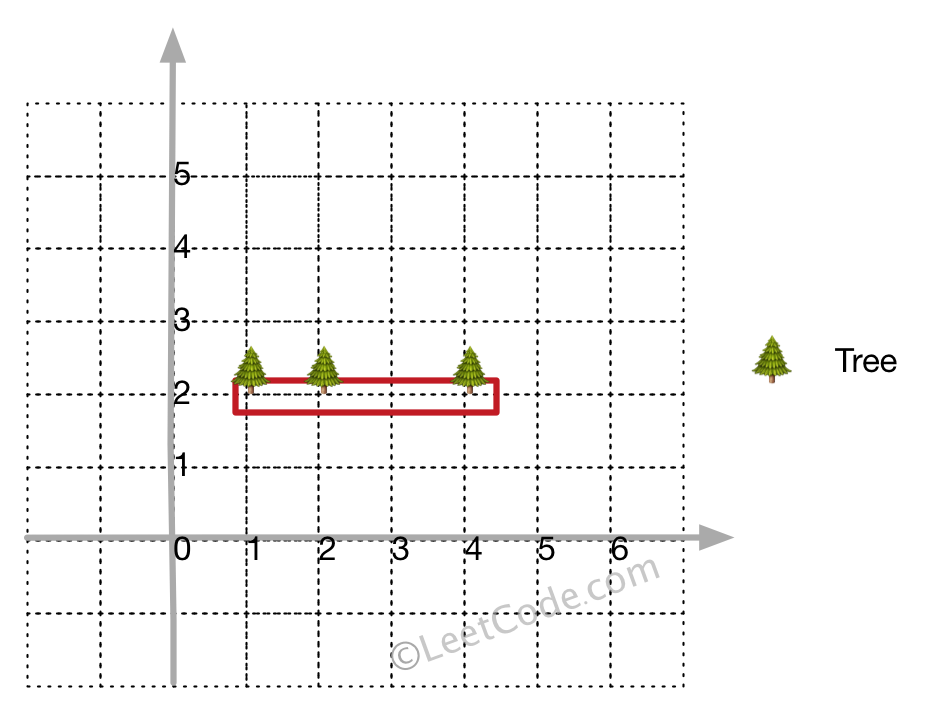 Even you only have trees in a line, you need to use rope to enclose them.
Even you only have trees in a line, you need to use rope to enclose them.