Massive Algorithms: LeetCode 572 - Subtree of Another Tree

LeetCode 572 - Subtree of Another Tree

https://leetcode.com/problems/subtree-of-another-tree

Given two non-empty binary trees s and t, check whether tree t has exactly the same structure and node values with a subtree of s. A subtree of s is a tree consists of a node in s and all of this node's descendants. The tree s could also be considered as a subtree of itself.

Example 1:
Given tree s:

Given tree t:

   4 
  / \
 1   2

Return true, because t has the same structure and node values with a subtree of s.

Example 2:
Given tree s:

Given tree t:

   4
  / \
 1   2

Return false.
X.
http://www.voidcn.com/article/p-ptciosva-p.html

 public boolean isSubtree(TreeNode s, TreeNode t) {
  StringBuilder sbd1 = new StringBuilder();
  StringBuilder sbd2 = new StringBuilder();
  preOrder(sbd1, s);
  preOrder(sbd2, t);
  return sbd1.toString().contains(sbd2);
 }

 private void preOrder(StringBuilder sbd, TreeNode t) {
  if(t == null) {
   sbd.append(",,");
   return;
  }  
  sbd.append(",").append(t.val);
  preOrder(sbd, t.left);
  preOrder(sbd, t.right);
 }

https://leetcode.com/articles/subtree-of-another-tree/

We can find the preorder traversal of the given tree

s

and

t

, given by, say

s_{preorder}

and

t_{preorder}

respectively(represented in the form of a string). Now, we can check if

t_{preorder}

is a substring of

s_{preorder}

But, in order to use this approach, we need to treat the given tree in a different manner. Rather than assuming a

null

value for the childern of the leaf nodes, we need to treat the left and right child as a

lnull

and

rnull

value respectively. This is done to ensure that the

t_{preorder}

doesn't become a substring of

s_{preorder}

even in cases when

t

isn't a subtree of

s

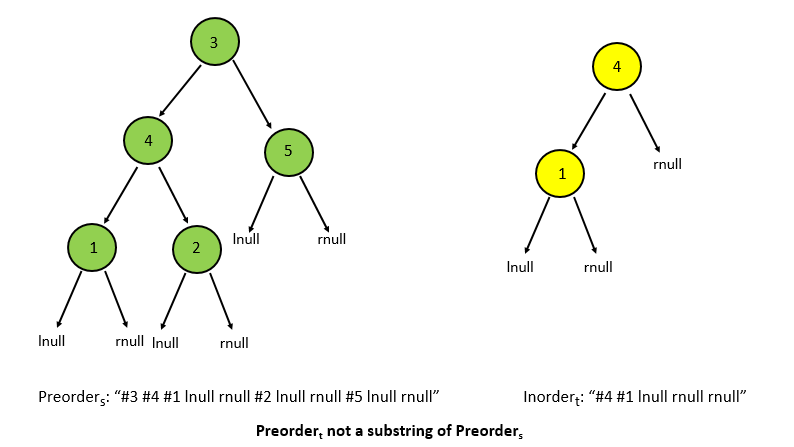
You can also note that we've added a '#' before every considering every value. If this isn't done, the trees of the form s:[23, 4, 5] and t:[3, 4, 5] will also give a true result since the preorder string of the t("23 4 lnull rull 5 lnull rnull") will be a substring of the preorder string of s("3 4 lnull rull 5 lnull rnull"). Adding a '#' before the node's value solves this problem.

HashSet<String> trees = new HashSet<>();

public boolean isSubtree(TreeNode s, TreeNode t) {

String tree1 = preorder(s, true);

String tree2 = preorder(t, true);

return tree1.indexOf(tree2) >= 0;

}

public String preorder(TreeNode t, boolean left) {

if (t == null) {

if (left)

return "lnull";

else

return "rnull";

}

return "#" + t.val + " " + preorder(t.left, true) + " " + preorder(t.right, false);

}

Time complexity : $O(m^2+n^2+m*n)$ . A total of $n$ nodes of the tree $s$ and $m$ nodes of tree $t$ are traversed. Assuming string concatenation takes $O(k)$ time for strings of length $k$ and indexOf takes $O(m*n)$ .
Space complexity : $O(max(m,n))$ . The depth of the recursion tree can go upto $n$ for tree $t$ and $m$ for tree $s$ in worst case.

https://leetcode.com/articles/subtree-of-another-tree/

We can find the preorder traversal of the given tree

s

and

t

, given by, say

s_{preorder}

and

t_{preorder}

respectively(represented in the form of a string). Now, we can check if

t_{preorder}

is a substring of

s_{preorder}

But, in order to use this approach, we need to treat the given tree in a different manner. Rather than assuming a

null

value for the childern of the leaf nodes, we need to treat the left and right child as a

lnull

and

rnull

value respectively. This is done to ensure that the

t_{preorder}

doesn't become a substring of

s_{preorder}

even in cases when

t

isn't a subtree of

s

    HashSet < String > trees = new HashSet < > ();
    public boolean isSubtree(TreeNode s, TreeNode t) {
        String tree1 = preorder(s, true);
        String tree2 = preorder(t, true);
        return tree1.indexOf(tree2) >= 0;
    }
    public String preorder(TreeNode t, boolean left) {
        if (t == null) {
            if (left)
                return "lnull";
            else
                return "rnull";
        }
        return "#"+t.val + " " +preorder(t.left, true)+" " +preorder(t.right, false);
    }

http://blog.csdn.net/fuxuemingzhu/article/details/71440802
StringBuilder spre = new StringBuilder(); StringBuilder tpre = new StringBuilder(); public boolean isSubtree(TreeNode s, TreeNode t) { preOrder(s, spre.append(",")); preOrder(t, tpre.append(",")); return spre.toString().contains(tpre.toString()); } public void preOrder(TreeNode root, StringBuilder str){ if(root == null){ str.append("#,"); return; } str.append(root.val).append(","); preOrder(root.left, str); preOrder(root.right, str); }

https://discuss.leetcode.com/topic/88700/easy-o-n-java-solution-using-inorder-and-preorder-traversal

 public boolean isSubtree(TreeNode s, TreeNode t) {
        String spreorder = generatepreorderString(s); 
        String tpreorder = generatepreorderString(t);
        
        return spreorder.contains(tpreorder) ;
    }
    public String generatepreorderString(TreeNode s){
        StringBuilder sb = new StringBuilder();
        Stack<TreeNode> stacktree = new Stack();
        stacktree.push(s);
        while(!stacktree.isEmpty()){
           TreeNode popelem = stacktree.pop();
           if(popelem==null)
              sb.append(",#"); // Appending # inorder to handle same values but not subtree cases
           else      
              sb.append(","+popelem.val);
           if(popelem!=null){
                stacktree.push(popelem.right);    
                stacktree.push(popelem.left);  
           }
        }
        return sb.toString();
    }

I don't think your code is guaranteed to be "O(n)." The String.contains() function in Java could be O(ST), where S and T are the sizes of two trees, or the sizes of two strings you generate (up to a multiplicative factor because of delimiters). Here's a reference:
http://stackoverflow.com/questions/4089558/what-is-the-big-o-of-string-contains-in-java

One of the best known algorithms is the Boyer-Moore string searching algorithm which is O(n) although it can give sublinear performance in the best case.

Which algorithm is used in Java depends on which implemetation you download. It seems that for example OpenJDK uses a naive algorithm that runs in O(nm) and linear performance in the best case.

https://discuss.leetcode.com/topic/88491/java-concise-o-n-m-time-o-n-m-space

public boolean isSubtree(TreeNode s, TreeNode t) {
    return serialize(s).contains(serialize(t)); // Java use a naive contains algorithm so to ensure linear time, 
                                                // replace with KMP algorithm
}

public String serialize(TreeNode root) {
    StringBuilder res = new StringBuilder();
    serialize(root, res);
    return res.toString();
}

private void serialize(TreeNode cur, StringBuilder res) {
    if (cur == null) {res.append(",#"); return;}
    res.append("," + cur.val);
    serialize(cur.left, res);
    serialize(cur.right, res);
}

Instead of creating an inorder traversal, we can treat every node of the given tree

t

as the root, treat it as a subtree and compare the corresponding subtree with the given subtree

s

for equality. For checking the equality, we can compare the all the nodes of the two subtrees.

For doing this, we make use a function traverse(s,t) which traverses over the given tree

s

and treats every node as the root of the subtree currently being considered. It also checks the two subtrees currently being considered for their equality. In order to check the equality of the two subtrees, we make use of equals(x,y) function, which takes

x

and

y

, which are the roots of the two subtrees to be compared as the inputs and returns True or False depending on whether the two are equal or not. It compares all the nodes of the two subtrees for equality. Firstly, it checks whether the roots of the two trees for equality and then calls itself recursively for the left subtree and the right subtree.

Time complexity : $O(m*n)$ . In worst case(skewed tree) traverse function takes $O(m*n)$ time.

https://discuss.leetcode.com/topic/88508/java-solution-tree-traversal

Because isSame method takes O(n) time and O(n) space. So the time complexity should be O(n ^ 2).

For each node during pre-order traversal of s, use a recursive function isSame to validate if sub-tree started with this node is the same with t.

    public boolean isSubtree(TreeNode s, TreeNode t) {
        if (s == null) return false;
        if (isSame(s, t)) return true;
        return isSubtree(s.left, t) || isSubtree(s.right, t);
    }
    
    private boolean isSame(TreeNode s, TreeNode t) {
        if (s == null && t == null) return true;
        if (s == null || t == null) return false;
        
        if (s.val != t.val) return false;
        
        return isSame(s.left, t.left) && isSame(s.right, t.right);
    }

X. https://leetcode.com/problems/subtree-of-another-tree/discuss/102755/Java-Solution-postorder-traversal-without-using-contains-O(N)

    public boolean isSubtree(TreeNode s, TreeNode t) {
        String tStr = getPostOrderString(t);
        return validateSubtree(s, tStr).find;
    }
    
    private String getPostOrderString(TreeNode root) {
        if(root==null) return "#";
        else {
            return getPostOrderString(root.left)+ "," +getPostOrderString(root.right) + "," + root.val;
        }
    }
    
    private State validateSubtree(TreeNode s, String tStr) {
        if(s==null) {
            boolean find = tStr.equals("#");
            return new State("#", find);
        }
        State left = validateSubtree(s.left, tStr);
        State right = validateSubtree(s.right, tStr);
        String str = left.str+","+right.str+","+s.val;
        boolean find = tStr.equals(str)||left.find||right.find;
        return new State(str, find);
    }
}

class State {
    String str;
    boolean find;
    public State(String str, boolean find) {
        this.str = str;
        this.find = find;
    }

X. https://shineboy2013.github.io/2018/01/29/lee-572/

如果s是BST，怎么改进算法？
二分法先找到s的节点值等于t根节点值的节点再比较。时间复杂度为O(logn+m)。

public boolean contains(TreeNode t, TreeNode node) {
 if (node == null)
  return false;
 int result = t.compareTo(node.val);
 if (result > 0)
  return contains(t, node.right);
 else if (result < 0)
  return contains(t, node.left);
 else
  return true;
}

若BST不是严格递增 (allow duplicates)，多比较几个相等节点即可。

The complexity of Java's implementation of indexOf is O(m*n) where n and m are the length of the search string and pattern respectively.

What you can do to improve complexity is to use e.g., the Boyer-More algorithm to intelligently skip comparing logical parts of the string which cannot match the pattern.

LeetCode 572 - Subtree of Another Tree

Labels

Popular Posts