LeetCode 964 - Least Operators to Express Number

https://leetcode.com/problems/least-operators-to-express-number/

Given a single positive integer x, we will write an expression of the form x (op1) x (op2) x (op3) x ... where each operator op1, op2, etc. is either addition, subtraction, multiplication, or division (+, -, *, or /).  For example, with x = 3, we might write 3 * 3 / 3 + 3 - 3 which is a value of 3.

When writing such an expression, we adhere to the following conventions:

1. The division operator (/) returns rational numbers.
2. There are no parentheses placed anywhere.
3. We use the usual order of operations: multiplication and division happens before addition and subtraction.
4. It's not allowed to use the unary negation operator (-).  For example, "x - x" is a valid expression as it only uses subtraction, but "-x + x" is not because it uses negation.

We would like to write an expression with the least number of operators such that the expression equals the given target.  Return the least number of operators used.

Example 1:

Input: x = 3, target = 19
Output: 5
Explanation: 3 * 3 + 3 * 3 + 3 / 3.  The expression contains 5 operations.

Example 2:

Input: x = 5, target = 501
Output: 8
Explanation: 5 * 5 * 5 * 5 - 5 * 5 * 5 + 5 / 5.  The expression contains 8 operations.

Example 3:

Input: x = 100, target = 100000000
Output: 3
Explanation: 100 * 100 * 100 * 100.  The expression contains 3 operations.

Note:

• 2 <= x <= 100
• 1 <= target <= 2 * 10^8

https://github.com/cherryljr/LeetCode/blob/master/Least%20Operators%20to%20Express%20Number.java

 * Approach: DP (Express Target Number in Base X)
 * 这道题目考察的是对 进制 方面的掌握和理解。但是在此基础上有进行了一个的升级，使得难度有所提高了。
 * 题目给出了一个 base number: x.需要我们通过对 x 进行四则运算最后得到 target.
 * 但是运算过程中不能有 括号。这点非常重要，因为这就以为着 除法 的用处只有一个：
 *  用来产生 1.除此之外其没有任何用处（因为题目要求的是使用最少的运算符）
 *  eg. x^2 = x * x = x * x * x / x
 *  毫无以为此时引入除法只会增加操作符的使用，带来负面影响
 * 那么根据以上条件，可以有如下表示：
 *  target = c0*x^0 + c1*x^1 + c2*x^2 + c3*x^3 + ... + cn*x^n,   -x < c < x
 * 因此最后我们需要求的结果就是：
 *  ops = 2*|c0| + 1*|c1| + 2*|c2| + 3*|c3| + ... + n*|cn| - 1
 * 这里注意到我们进行了一次 -1 操作。
 * 这是因为，我们以上所有的操作都是带符号进行运算的。
 * 但是表达式第一项的符号是可以省略掉的。可能有人会有疑问：负号的话就不能省略了。
 * 然而根据题目的数据范围可知：x 与 target 均为 正整数。
 * 因此表达式中必定至少存在一项正的，所以我们可以把 负的这一项 移到后面去，这样就能省略掉一个操作符了。
 * 同时，对于第一项，我们这里 *2，这是因为要产生一个 1，或者是 -1.我们都需要两个操作符。（±x/x）
 *
 * 此外，我们还需要知道非常重要的一点就是：
 *  target 可以由比较小的数叠加而来，而可以由比较大的数减去一个值得到。
 * 而我们需要求的就是最短的路径（最少需要多少个操作符）。
 * 因此这里实际上是一个 DP 问题，即我们只关心由 x 经过运算得到某一个值 n 最少需要的操作符个数。
 * 但是并不关心中间的具体操作过程（无后效性问题）。
 *  eg. x = 3, target = 7
 *  target = 3*3 - 3/3 - 3/3, ops = 5
 *  target = 3 + 3 + 3/3 , ops = 3
 *  （注意：7的三进制是 21）即：7 = 2*3^1 + 1 * 3^0, 对于 ops = 2 * 1 + 2 - 1 = 3

X. https://leetcode.com/problems/least-operators-to-express-number/discuss/208428/Java-DFS-with-memoization

Inspired by the race car problem. Only need to consider two candidates. But unfortunately I cannot give mathematical prove of the correntness.

    Map<Integer, Integer> memo = new HashMap<>();
    public int leastOpsExpressTarget(int x, int target) {
        if (target == 1) 
            return x == 1 ? 0 : 1;
        if (memo.containsKey(target))
            return memo.get(target);
        long product = x;
        int count = 0;
        while (product < target) {
            count++;
            product *= x;
            
        }
        
        // candidate1 : in the form : x*x*...*x - (......) = target
        int cand1 = Integer.MAX_VALUE;
        if (product == target)
            cand1 = count;
        else if (product - target < target)
            cand1 = count + leastOpsExpressTarget(x, (int)(product - target)) + 1;
        
        // candidate2 : in the form : x*x*...*x + (......) = target
        int cand2 = Integer.MAX_VALUE;
        product /= x;
        cand2 = leastOpsExpressTarget(x, (int)(target - product)) + (count == 0 ? 2 : count);
        int res = Math.min(cand1, cand2);
        memo.put(target, res);
        return res;
    }

X. DFS + cache

Time complexity: O(x * log(t)/log(x))
Space complexity: O(x * log(t)/log(x))

  int leastOpsExpressTarget(int x, int target) {

    return dp(x, target);

  }

private:

  unordered_map<int, int> m_;

  int dp(int x, int t) {

    if (t == 0) return 0;

    if (t < x) return min(2 * t - 1, 2 * (x - t));

    if (m_.count(t)) return m_.at(t);

    int k = log(t) / log(x);

    long p = pow(x, k);

    if (t == p) return m_[t] = k - 1;

    int ans = dp(x, t - p) + k; // t - p < t

    long left = p * x - t;

    if (left < t) // only rely on smaller sub-problems

      ans = min(ans, dp(x, left) + k + 1);

    return m_[t] = ans;

  }

https://leetcode.com/problems/least-operators-to-express-number/discuss/208475/Java-DFS-with-memo

  Map<String, Integer> memo;

  int x;

  public int leastOpsExpressTarget(int x, int target) {

    memo = new HashMap();

    this.x = x;

    return dp(0, target) - 1;

  }

  public int dp(int i, int target) {

    String code = "" + i + "#" + target;

    if (memo.containsKey(code))

      return memo.get(code);

    int ans;

    if (target == 0) {

      ans = 0;

    } else if (target == 1) {

      ans = cost(i);

    } else if (i >= 39) {

      ans = target + 1;

    } else {

      int t = target / x;

      int r = target % x;

      ans = Math.min(r * cost(i) + dp(i + 1, t), (x - r) * cost(i) + dp(i + 1, t + 1));

    }

    memo.put(code, ans);

    return ans;

  }

  public int cost(int x) {

    return x > 0 ? x : 2;

  }

https://zhanghuimeng.github.io/post/leetcode-964-least-operators-to-express-number/

这道题在本质上非常类似于进制表示：

$$target=a_0+a_{1}x+a_2{x}^2+\cdots$$

但是很大的一个区别在于，它对系数（理论上）没有限制，也因此对$x$的最大幂次没有限制（因为系数可以是负的）。而且我们的目标是最小化代价。容易推断出，生成一个$x$的幂次的代价为（包含前面的+/-运算符）：

$$cost\left(x^e\right)=\{\begin{array}{cc}2& e=0\\ e& e\ge 1\end{array}$$

显然，如果要生成一个$a_e{x}^e$，最优的选择是都采用+或者都采用-运算符（因为同时用显然是浪费）。

因此整体的代价可以表示为

$$cost=2\cdot abs\left(a_0\right)+2\cdot abs\left(a_1\right)+3\cdot abs\left(a_2\right)+\cdots$$

不妨首先把$target$表示成普通的$x$进制的形式：

$$target=b_0+b_{1}x+b_2{x}^2+\cdots +b_n{x}^n,,0\le b_i<x$$

可以认为$a_i$是在$b_i$的基础上得到的，例如：

$$target=(b_0-x+x^2)+(b_1+1)x+(b_2-1)x^2+\cdots$$

这个式子看起来好像借位，不过比实际中的借位要自由，因为现实的进制中不会出现$b_0$这一位向$b_2$借位的情况。

此时有$a_0=b_0-x+x^2,,a_1=b_1+1,,a_2=b_2-1$。显然此时整体的代价也变化了：

$$cost=2b_0+2b_1+3b_2+\cdots$$

$$cos{t}^{\prime }=2\cdot |b_0-x+x^2|+2\cdot |b_1+1|+3\cdot |b_2-1|+\cdots$$

显然我们希望整体代价最小。考虑到$x>=2$，显然可以得出这样一个结论：从比前一位更往前的位借位是不值得的，而且一定是借一个负位。原因很简单：假定$b_i$从$b_j$借了$k$位（$j\ge i+2$），则这两位的cost之和从$|b_i|(i+1)+|b_j|(j+1)$变成了$|b_i+k{x}^{j-i}|(i+1)+|b_j-k|(j+1)$。通过各种分类讨论可以发现，这个cost不可能减小。（懒得去讨论了……）

所以可以用递推的方法来考虑这个问题：令

$$\begin{array}{cc}f\left[i\right]\left[0\right]=& mincost(a_0+a_{1}x+a_2{x}^2+\cdots +a_i{x}^i)\\ f\left[i\right]\left[1\right]=& mincost(a_0+a_{1}x+a_2{x}^2+\cdots +(a_i-x\left)x^i\right)\end{array}$$

也就是说$f\left[i\right]\left[1\right]$是借了一个负位之后最小可能的表示的代价。则

$$\begin{array}{cc}f[i+1]\left[0\right]=& mincost(a_0+a_{1}x+a_2{x}^2+\cdots +a_i{x}^i+a_{i+1}{x}^{i+1})\\ =& mincost(a_0+a_{1}x+a_2{x}^2+\cdots +a_i{x}^i)+cost\left(a_{i+1}{x}^{i+1}\right),\\ & cost(a_0+a_{1}x+a_2{x}^2+\cdots +(a_i-x\left)x^i\right)+cost\left(\right(a_{i+1}+1\left)x^{i+1}\right)\\ =& minf\left[i\right]\left[0\right]+a_{i+1}(i+1),f\left[i\right]\left[1\right]+(a_{i+1}+1)(i+1)\end{array}$$

同理：

$$f[i+1]\left[1\right]=minf\left[i\right]\left[0\right]+|a[i+1]-x|(i+1),f\left[i\right]\left[1\right]+|a[i+1]-x+1|(i+1)$$

然后就可以递推了，时间复杂度为O(log(N))。

从借位的想法translate到递推还是不太容易啊……

以及，考虑到有借位的可能，需要递推到f[n]，而不是f[n-1]。

    int leastOpsExpressTarget(int x, int target) {
        int a[1000], n = 0;
        memset(a, 0, sizeof(a));
        int t = target;
        while (t > 0) {
            a[n++] = t % x;
            t /= x;
        }
        int f[1000][2];
        f[0][0] = 2 * a[0];
        f[0][1] = 2 * abs(a[0] - x);
        for (int i = 1; i <= n; i++) {
            f[i][0] = min(f[i-1][0] + a[i] * i, f[i-1][1] + (a[i] + 1) * i);
            f[i][1] = min(f[i-1][0] + abs(a[i] - x) * i, f[i-1][1] + abs(a[i] - x + 1) * i);
        }
        return f[n][0] - 1;
    }

X.
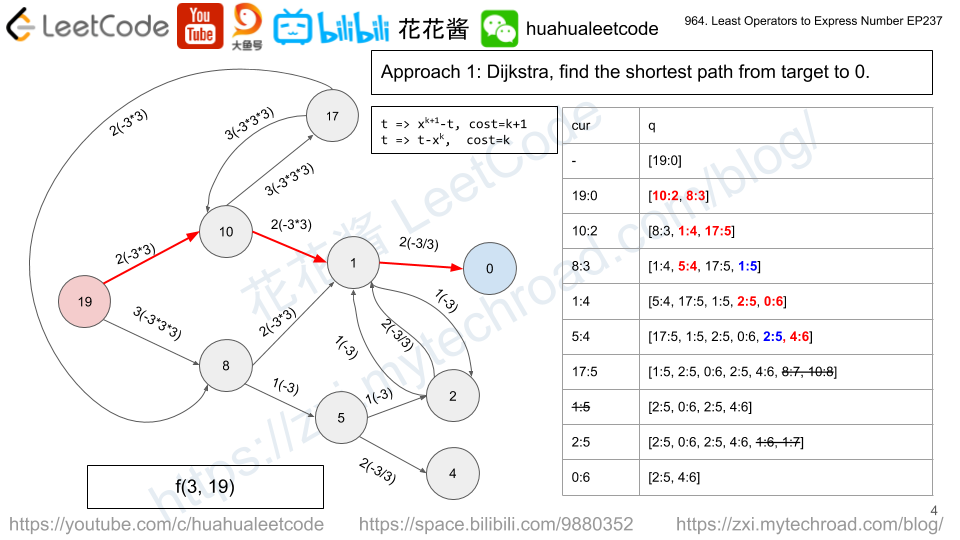
https://zxi.mytechroad.com/blog/uncategorized/leetcode-964-least-operators-to-express-number/
Dijkstra

Find the shortest path from target to 0 using ops.

Time complexity: O(nlogn)
Space complexity: O(nlogn) 
n = x * log(t) / log(x)

    int leastOpsExpressTarget(int x, int target) {

      priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;

      unordered_set<int> s;

      q.emplace(0, target);

      while (!q.empty()) {

        const int c = q.top().first;

        const int t = q.top().second;

        q.pop();

        if (t == 0) return c - 1;

        if (s.count(t)) continue;

        s.insert(t);

        int n = log(t) / log(x);

        int l = t - pow(x, n);        

        q.emplace(c + (n == 0 ? 2 : n), l);

        int r = pow(x, n + 1) - t;        

        q.emplace(c + n + 1, r);

      }

      return -1;

    }