KMP - Summary

https://www.cnblogs.com/tangzhengyue/p/4315393.html

这个图画的就是strKey这个要查找的关键字字符串。假设我们有一个空的next数组，我们的工作就是要在这个next数组中填值。
下面我们用数学归纳法来解决这个填值的问题。
这里我们借鉴数学归纳法的三个步骤（或者说是动态规划？）：
1、初始状态
2、假设第j位以及第j位之前的我们都填完了
3、推论第j+1位该怎么填

初始状态我们稍后再说，我们这里直接假设第j位以及第j位之前的我们都填完了。也就是说，从上图来看，我们有如下已知条件：
next[j] == k;
next[k] == 绿色色块所在的索引;
next[绿色色块所在的索引] == 黄色色块所在的索引;
这里要做一个说明：图上的色块大小是一样的（没骗我？好吧，请忽略色块大小，色块只是代表数组中的一位）。

我们来看下面一个图，可以得到更多的信息：

1.由"next[j] == k;"这个条件，我们可以得到A1子串 == A2子串（根据next数组的定义，前后缀那个）。

2.由"next[k] == 绿色色块所在的索引;"这个条件，我们可以得到B1子串 == B2子串。

3.由"next[绿色色块所在的索引] == 黄色色块所在的索引;"这个条件，我们可以得到C1子串 == C2子串。

4.由1和2(A1 == A2，B1 == B2)可以得到B1 == B2 == B3。

5.由2和3(B1 == B2， C1 == C2)可以得到C1 == C2 == C3。

6.B2 == B3可以得到C3 == C4 == C1 == C2

上面这个就是很简单的几何数学，仔细看看都能看懂的。我这里用相同颜色的线段表示完全相同的子数组，方便观察。

http://jakeboxer.com/blog/2009/12/13/the-knuth-morris-pratt-algorithm-in-my-own-words/
https://www.cnblogs.com/c-cloud/p/3224788.html

 1 void makeNext(const char P[],int next[])
 2 {
 3     int q,k;//q:模版字符串下标；k:最大前后缀长度
 4     int m = strlen(P);//模版字符串长度
 5     next[0] = 0;//模版字符串的第一个字符的最大前后缀长度为0
 6     for (q = 1,k = 0; q < m; ++q)//for循环，从第二个字符开始，依次计算每一个字符对应的next值
 7     {
 8         while(k > 0 && P[q] != P[k])//递归的求出P[0]···P[q]的最大的相同的前后缀长度k
 9             k = next[k-1];          //不理解没关系看下面的分析，这个while循环是整段代码的精髓所在，确实不好理解  
10         if (P[q] == P[k])//如果相等，那么最大相同前后缀长度加1
11         {
12             k++;
13         }
14         next[q] = k;
15     }
16 } 

 　　现在我着重讲解一下while循环所做的工作：

1. 　　已知前一步计算时最大相同的前后缀长度为k（k>0），即P[0]···P[k-1]；
2. 　　此时比较第k项P[k]与P[q],如图1所示
3. 　　如果P[K]等于P[q]，那么很简单跳出while循环;
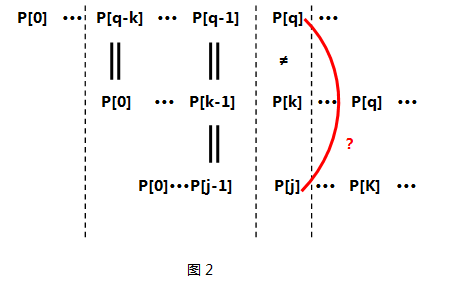
4. 　　关键！关键有木有！关键如果不等呢？？？那么我们应该利用已经得到的next[0]···next[k-1]来求P[0]···P[k-1]这个子串中最大相同前后缀，可能有同学要问了——为什么要求P[0]···P[k-1]的最大相同前后缀呢？？？是啊！为什么呢？ 原因在于P[k]已经和P[q]失配了，而且P[q-k] ··· P[q-1]又与P[0] ···P[k-1]相同，看来P[0]···P[k-1]这么长的子串是用不了了，那么我要找个同样也是P[0]打头、P[k-1]结尾的子串即P[0]···P[j-1](j==next[k-1])，看看它的下一项P[j]是否能和P[q]匹配。如图2所示

 

https://www.geeksforgeeks.org/kmp-algorithm-for-pattern-searching/

The KMP matching algorithm uses degenerating property (pattern having same sub-patterns appearing more than once in the pattern) of the pattern and improves the worst case complexity to O(n). The basic idea behind KMP’s algorithm is: whenever we detect a mismatch (after some matches), we already know some of the characters in the text of the next window. We take advantage of this information to avoid matching the characters that we know will anyway match. Let us consider below example to understand this.

• KMP algorithm preprocesses pat[] and constructs an auxiliary lps[] of size m (same as size of pattern) which is used to skip characters while matching.
• name lps indicates longest proper prefix which is also suffix.. A proper prefix is prefix with whole string not allowed. For example, prefixes of “ABC” are “”, “A”, “AB” and “ABC”. Proper prefixes are “”, “A” and “AB”. Suffixes of the string are “”, “C”, “BC” and “ABC”.
• We search for lps in sub-patterns. More clearly we focus on sub-strings of patterns that are either prefix and suffix.
• For each sub-pattern pat[0..i] where i = 0 to m-1, lps[i] stores length of the maximum matching proper prefix which is also a suffix of the sub-pattern pat[0..i].

     lps[i] = the longest proper prefix of pat[0..i] 
                which is also a suffix of pat[0..i]. 

Note : lps[i] could also be defined as longest prefix which is also proper suffix. We need to use properly at one place to make sure that the whole substring is not considered.

How to use lps[] to decide next positions (or to know a number of characters to be skipped)?
• We start comparison of pat[j] with j = 0 with characters of current window of text.
• We keep matching characters txt[i] and pat[j] and keep incrementing i and j while pat[j] and txt[i] keep matching.
• When we see a mismatch
  • We know that characters pat[0..j-1] match with txt[i-j…i-1] (Note that j starts with 0 and increment it only when there is a match).
  • We also know (from above definition) that lps[j-1] is count of characters of pat[0…j-1] that are both proper prefix and suffix.
  • From above two points, we can conclude that we do not need to match these lps[j-1] characters with txt[i-j…i-1] because we know that these characters will anyway match. 
void KMPSearch(char* pat, char* txt)
{
    int M = strlen(pat);
    int N = strlen(txt);
  
    // create lps[] that will hold the longest prefix suffix
    // values for pattern
    int lps[M];
  
    // Preprocess the pattern (calculate lps[] array)
    computeLPSArray(pat, M, lps);
  
    int i = 0; // index for txt[]
    int j = 0; // index for pat[]
    while (i < N) {
        if (pat[j] == txt[i]) {
            j++;
            i++;
        }
  
        if (j == M) {
            printf("Found pattern at index %d ", i - j);
            j = lps[j - 1];
        }
  
        // mismatch after j matches
        else if (i < N && pat[j] != txt[i]) {
            // Do not match lps[0..lps[j-1]] characters,
            // they will match anyway
            if (j != 0)
                j = lps[j - 1];
            else
                i = i + 1;
        }
    }
}
  
// Fills lps[] for given patttern pat[0..M-1]
void computeLPSArray(char* pat, int M, int* lps)
{
    // length of the previous longest prefix suffix
    int len = 0;
  
    lps[0] = 0; // lps[0] is always 0
  
    // the loop calculates lps[i] for i = 1 to M-1
    int i = 1;
    while (i < M) {
        if (pat[i] == pat[len]) {
            len++;
            lps[i] = len;
            i++;
        }
        else // (pat[i] != pat[len])
        {
            // This is tricky. Consider the example.
            // AAACAAAA and i = 7. The idea is similar
            // to search step.
            if (len != 0) {
                len = lps[len - 1];
  
                // Also, note that we do not increment
                // i here
            }
            else // if (len == 0)
            {
                lps[i] = 0;
                i++;
            }
        }
    }
}