https://leetcode.com/problems/odd-even-jump/
X.
https://leetcode.com/problems/odd-even-jump/discuss/217981/JavaC%2B%2BPython-DP-idea-Using-TreeMap-or-Stack
Time Complexity: , where is the length of
Approach 1: Monotonic Stack
You are given an integer array
A. From some starting index, you can make a series of jumps. The (1st, 3rd, 5th, ...) jumps in the series are called odd numbered jumps, and the (2nd, 4th, 6th, ...) jumps in the series are called even numbered jumps.
You may from index
i jump forward to index j (with i < j) in the following way:- During odd numbered jumps (ie. jumps 1, 3, 5, ...), you jump to the index j such that
A[i] <= A[j]andA[j]is the smallest possible value. If there are multiple such indexesj, you can only jump to the smallest such indexj. - During even numbered jumps (ie. jumps 2, 4, 6, ...), you jump to the index j such that
A[i] >= A[j]andA[j]is the largest possible value. If there are multiple such indexesj, you can only jump to the smallest such indexj. - (It may be the case that for some index
i,there are no legal jumps.)
A starting index is good if, starting from that index, you can reach the end of the array (index
A.length - 1) by jumping some number of times (possibly 0 or more than once.)
Return the number of good starting indexes.
Example 1:
Input: [10,13,12,14,15] Output: 2 Explanation: From starting index i = 0, we can jump to i = 2 (since A[2] is the smallest among A[1], A[2], A[3], A[4] that is greater or equal to A[0]), then we can't jump any more. From starting index i = 1 and i = 2, we can jump to i = 3, then we can't jump any more. From starting index i = 3, we can jump to i = 4, so we've reached the end. From starting index i = 4, we've reached the end already. In total, there are 2 different starting indexes (i = 3, i = 4) where we can reach the end with some number of jumps.
X.
https://leetcode.com/problems/odd-even-jump/discuss/217981/JavaC%2B%2BPython-DP-idea-Using-TreeMap-or-Stack
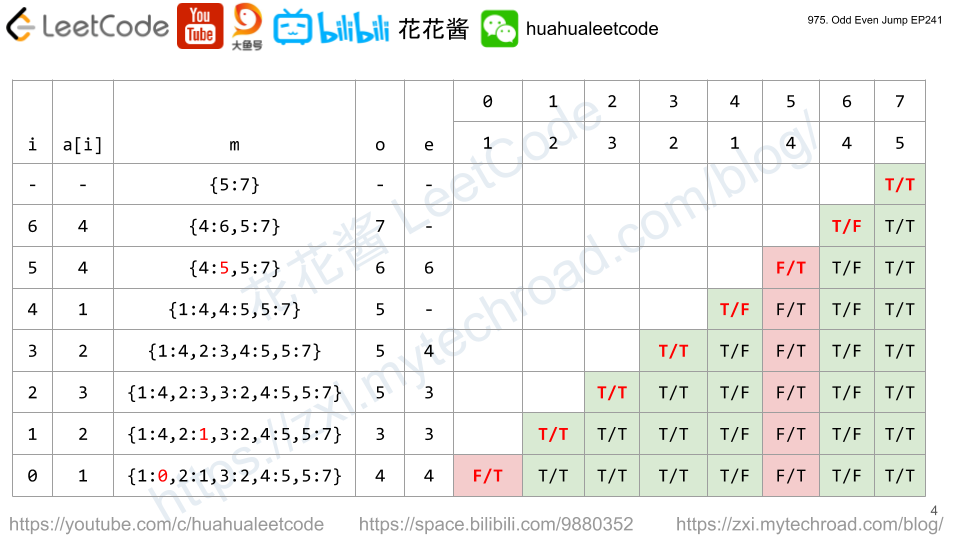
We need to jump higher and lower alternately to the end.
Take [5,1,3,4,2] as example.
If we start at 2,
we can jump either higher first or lower first to the end,
because we are already at the end.
higher(2) = true
lower(2) = true
we can jump either higher first or lower first to the end,
because we are already at the end.
higher(2) = true
lower(2) = true
If we start at 4,
we can't jump higher, higher(4) = false
we can jump lower to 2, lower(4) = higher(2) = true
we can't jump higher, higher(4) = false
we can jump lower to 2, lower(4) = higher(2) = true
If we start at 3,
we can jump higher to 4, higher(3) = lower(4) = true
we can jump lower to 2, lower(3) = higher(2) = true
we can jump higher to 4, higher(3) = lower(4) = true
we can jump lower to 2, lower(3) = higher(2) = true
If we start at 1,
we can jump higher to 2, higher(1) = lower(2) = true
we can't jump lower, lower(1) = false
we can jump higher to 2, higher(1) = lower(2) = true
we can't jump lower, lower(1) = false
If we start at 5,
we can't jump higher, higher(5) = false
we can jump lower to 4, lower(5) = higher(4) = false
we can't jump higher, higher(5) = false
we can jump lower to 4, lower(5) = higher(4) = false
public int oddEvenJumps(int[] A) {
int n = A.length, res = 1;
boolean[] higher = new boolean[n], lower = new boolean[n];
higher[n - 1] = lower[n - 1] = true;
TreeMap<Integer, Integer> map = new TreeMap<>();
map.put(A[n - 1], n - 1);
for (int i = n - 2; i >= 0; --i) {
Map.Entry hi = map.ceilingEntry(A[i]), lo = map.floorEntry(A[i]);
if (hi != null) higher[i] = lower[(int)hi.getValue()];
if (lo != null) lower[i] = higher[(int)lo.getValue()];
if (higher[i]) res++;
map.put(A[i], i);
}
return res;
}
First let's create a boolean DP array.
dp[i][0] stands for you can arrive index
dp[i][1] stands for you can arrive index
Index n - 1 is always a good start point, regardless it's odd or even step right now. Thus dp[n - 1][0] = dp[n - 1][1] =
dp[i][0] = dp[index_next_greater_number][1] - because next is even step
dp[i][1] = dp[index_next_smaller_number][0] - because next is odd step
Since first step is odd step, then result is count of dp[i][0] with value
dp[i][0] stands for you can arrive index
n - 1 starting from index i at an odd step.dp[i][1] stands for you can arrive index
n - 1 starting from index i at an even step.Initialization:Index n - 1 is always a good start point, regardless it's odd or even step right now. Thus dp[n - 1][0] = dp[n - 1][1] =
true.DP formula:dp[i][0] = dp[index_next_greater_number][1] - because next is even step
dp[i][1] = dp[index_next_smaller_number][0] - because next is odd step
Result:Since first step is odd step, then result is count of dp[i][0] with value
true.
To quickly find the next greater or smaller number and its index: traverse the array reversely and store data into a
TreeMap using the number as Key and its index as Value.
Time complexity O(nlgn), Space complexity O(n). n is the length of the array.
public int oddEvenJumps(int[] A) {
int n = A.length;
TreeMap<Integer, Integer> map = new TreeMap<>();
boolean[][] dp = new boolean[n][2];
dp[n - 1][0] = true;
dp[n - 1][1] = true;
map.put(A[n - 1], n - 1);
int res = 1;
for (int i = n - 2; i >= 0; i--) {
// Odd step
Integer nextGreater = map.ceilingKey(A[i]);
if (nextGreater != null) {
dp[i][0] = dp[map.get(nextGreater)][1];
}
// Even step
Integer nextSmaller = map.floorKey(A[i]);
if (nextSmaller != null) {
dp[i][1] = dp[map.get(nextSmaller)][0];
}
map.put(A[i], i);
res += dp[i][0] ? 1 : 0;
}
return res;
}
As in Approach 1, the problem reduces to solving this question: for some index
i during an odd numbered jump, what index do we jump to (if any)?
Algorithm
We can use a
TreeMap, which is an excellent structure for maintaining sorted data. Our map vals will map values v = A[i] to indices i.
Iterating from
i = N-2 to i = 0, we have some value v = A[i] and we want to know what the next largest or next smallest value is. The TreeMap.lowerKey and TreeMap.higherKey functions do this for us.
With this in mind, the rest of the solution is straightforward: we use dynamic programming to maintain
odd[i] and even[i]: whether the state of being at index i on an odd or even numbered jump is possible to reach
public int oddEvenJumps(int[] A) {
int N = A.length;
if (N <= 1)
return N;
boolean[] odd = new boolean[N];
boolean[] even = new boolean[N];
odd[N - 1] = even[N - 1] = true;
TreeMap<Integer, Integer> vals = new TreeMap();
vals.put(A[N - 1], N - 1);
for (int i = N - 2; i >= 0; --i) {
int v = A[i];
if (vals.containsKey(v)) {
odd[i] = even[vals.get(v)];
even[i] = odd[vals.get(v)];
} else {
Integer lower = vals.lowerKey(v);
Integer higher = vals.higherKey(v);
if (lower != null)
even[i] = odd[vals.get(lower)];
if (higher != null) {
odd[i] = even[vals.get(higher)];
}
}
vals.put(v, i);
}
int ans = 0;
for (boolean b : odd)
if (b)
ans++;
return ans;
}
https://leetcode.com/articles/odd-even-jump/Time Complexity: , where is the length of
A.Approach 1: Monotonic Stack
Intuition
First, we notice that where you jump to is determined only by the state of your current index and the jump number parity.
For each state, there is exactly one state you could jump to (or you can't jump.) If we somehow knew these jumps, we could solve the problem by a simple traversal.
So the problem reduces to solving this question: for some index
i during an odd numbered jump, what index do we jump to (if any)? The question for even-numbered jumps is similar.
Algorithm
Let's figure out where index
i jumps to, assuming this is an odd-numbered jump.
Let's consider each value of
A in order from smallest to largest. When we consider a value A[j] = v, we search the values we have already processed (which are <= v) from largest to smallest. If we find that we have already processed some value v0 = A[i] with i < j, then we know i jumps to j.
Naively this is a little slow, but we can speed this up with a common trick for harder problems: a monotonic stack. (For another example of this technique, please see the solution to this problem: (Article - Sum of Subarray Minimums))
Let's store the indices
i of the processed values v0 = A[i] in a stack, and maintain the invariant that this is monotone decreasing. When we add a new index j, we pop all the smaller indices i < j from the stack, which all jump to j.
Afterwards, we know
oddnext[i], the index where i jumps to if this is an odd numbered jump. Similarly, we know evennext[i]. We can use this information to quickly build out all reachable states using dynamic programming.
class Solution(object):
def oddEvenJumps(self, A):
N = len(A)
def make(B):
ans = [None] * N
stack = [] # invariant: stack is decreasing
for i in B:
while stack and i > stack[-1]:
ans[stack.pop()] = i
stack.append(i)
return ans
B = sorted(range(N), key = lambda i: A[i])
oddnext = make(B)
B.sort(key = lambda i: -A[i])
evennext = make(B)
odd = [False] * N
even = [False] * N
odd[N-1] = even[N-1] = True
for i in xrange(N-2, -1, -1):
if oddnext[i] is not None:
odd[i] = even[oddnext[i]]
if evennext[i] is not None:
even[i] = odd[evennext[i]]
return sum(odd)
int oddEvenJumps(vector<int>& A) { int n = A.size(); int odd[n], even[n]; stack<pair<int, int>> s; vector<pair<int, int>> indices; for (int i = 0; i < n; i++) indices.emplace_back(A[i], -i); sort(indices.begin(), indices.end()); for (int i = 0; i < n; i++) indices[i].second = -indices[i].second; for (int i = 0; i < n; i++) { while (!s.empty() && indices[i].second > s.top().second) { s.pop(); } if (s.empty()) even[indices[i].second] = -1; else even[indices[i].second] = s.top().second; s.push(indices[i]); } s = stack<pair<int, int>>(); indices.clear(); for (int i = 0; i < n; i++) indices.emplace_back(A[i], i); sort(indices.begin(), indices.end()); for (int i = n - 1; i >= 0; i--) { while (!s.empty() && indices[i].second > s.top().second) s.pop(); if (s.empty()) odd[indices[i].second] = -1; else odd[indices[i].second] = s.top().second; s.push(indices[i]); } int oddjump[n], evenjump[n]; int ans = 0; for (int i = n - 1; i >= 0; i--) { if (odd[i] != -1) oddjump[i] = evenjump[odd[i]]; else oddjump[i] = i; if (even[i] != -1) evenjump[i] = oddjump[even[i]]; else evenjump[i] = i; if (oddjump[i] == n - 1) ans++; } return ans; }
In Python, I used stack to find next_higher and next_lower
def oddEvenJumps(self, A):
n = len(A)
next_higher, next_lower = [0] * n, [0] * n
stack = []
for a, i in sorted([a, i] for i, a in enumerate(A)):
while stack and stack[-1] < i:
next_higher[stack.pop()] = i
stack.append(i)
stack = []
for a, i in sorted([-a, i] for i, a in enumerate(A)):
while stack and stack[-1] < i:
next_lower[stack.pop()] = i
stack.append(i)
higher, lower = [0] * n, [0] * n
higher[-1] = lower[-1] = 1
for i in range(n - 1)[::-1]:
higher[i] = lower[next_higher[i]]
lower[i] = higher[next_lower[i]]
return sum(higher)
X. DP + Get next greater/smaller