https://leetcode.com/problems/tallest-billboard/
https://leetcode.com/problems/tallest-billboard/discuss/203181/JavaC%2B%2BPython-DP-min(O(SN2)-O(3N2-*-N)
For example, if have a pair of sum
If we have
And this is the biggest pair with difference = a
X.
https://leetcode.com/problems/tallest-billboard/discuss/204232/Simplest-DP-solution-which-is-easy-to-understand
https://zxi.mytechroad.com/blog/dynamic-programming/leetcode-956-tallest-billboard/
https://www.acwing.com/solution/LeetCode/content/644/
状态 f(i,j)f(i,j) 表示考虑了前 ii 个钢筋,搭建的两个钢制支架差距为 jj 时,较低的支架 的最大高度是多少。
初始化 f(i,j)=−∞f(i,j)=−∞,f(0,0)=0f(0,0)=0。
转移时,如果不用第 ii 个钢筋,则 f(i,j)=max(f(i,j),f(i−1,j))f(i,j)=max(f(i,j),f(i−1,j));如果使用了第 ii 个钢筋,并将它放到了较高的支架上,则差距会扩大 rods[i],即 f(i,j+x)=max(f(i,j+x),f(i−1,j))f(i,j+x)=max(f(i,j+x),f(i−1,j));若放到了较低的支架上,并且差距 jj 小于等于 rods[i],则 f(i,j−x)=max(f(i,j−x),f(i−1,j)+x)f(i,j−x)=max(f(i,j−x),f(i−1,j)+x),否则 f(i,x−j)=max(f(i,x−j),f(i−1,j)+j)f(i,x−j)=max(f(i,x−j),f(i−1,j)+j)。
最终答案为 f(n,0)f(n,0)。
int tallestBillboard(vector<int>& rods) {
int n = rods.size(), sum = 0;
vector<vector<int>> f(n + 1, vector<int>(5010, -5010));
f[0][0] = 0;
for (int i = 1; i <= n; i++) {
sum += rods[i - 1];
for (int j = 0; j <= sum; j++) {
f[i][j] = max(f[i][j], f[i - 1][j]);
int x = rods[i - 1];
if (j + x <= sum)
f[i][j + x] = max(f[i][j + x], f[i - 1][j]);
if (x <= j)
f[i][j - x] = max(f[i][j - x], f[i - 1][j] + x);
else
f[i][x - j] = max(f[i][x - j], f[i - 1][j] + j);
}
}
return f[n][0];
}
X.
解法2:中间相遇法
https://blog.csdn.net/xx_123_1_rj/article/details/86557102
You are installing a billboard and want it to have the largest height. The billboard will have two steel supports, one on each side. Each steel support must be an equal height.
You have a collection of
rods which can be welded together. For example, if you have rods of lengths 1, 2, and 3, you can weld them together to make a support of length 6.
Return the largest possible height of your billboard installation. If you cannot support the billboard, return 0.
Example 1:
Input: [1,2,3,6] Output: 6 Explanation: We have two disjoint subsets {1,2,3} and {6}, which have the same sum = 6.
Example 2:
Input: [1,2,3,4,5,6] Output: 10 Explanation: We have two disjoint subsets {2,3,5} and {4,6}, which have the same sum = 10.
Example 3:
Input: [1,2] Output: 0 Explanation: The billboard cannot be supported, so we return 0.
Note:
0 <= rods.length <= 201 <= rods[i] <= 1000The sum of rods is at most 5000
https://leetcode.com/problems/tallest-billboard/discuss/203181/JavaC%2B%2BPython-DP-min(O(SN2)-O(3N2-*-N)
dp[d]dFor example, if have a pair of sum
(a, b) with a > b, then dp[a - b] = bIf we have
dp[diff] = a, it means we have a pair of sum (a, a + diff).And this is the biggest pair with difference = a
dp is initializes with dp[0] = 0;
Assume we have an init state like this
------- y ------|----- d -----|
------- y ------|
------- y ------|----- d -----|
------- y ------|
case 1
If put
------- y ------|----- d -----|----- x -----|
------- y ------|
If put
x to tall side------- y ------|----- d -----|----- x -----|
------- y ------|
We update
dp[d + x] = max(dp[d + x], y )
case 2.1
Put
-------y------|----- d -----|
-------y------|--- x ---|
Put
x to low side and d >= x:-------y------|----- d -----|
-------y------|--- x ---|
We update
dp[d-x] = max( dp[d - x], y + x)
case 2.2
Put
------- y ------|----- d -----|
------- y ------|------- x -------|
We update
Put
x to low side and d < x:------- y ------|----- d -----|
------- y ------|------- x -------|
We update
dp[x - d] = max(dp[x - d], y + d)
case 2.1 and case2.2 can merge into
dp[abs(x - d)] = max(dp[abs(x - d)], y + min(d, x))Time Complexity:
O(NM), where we haveN = rod.length <= 20S = sum(rods) <= 5000M = all possible sum = min(3^N, S)
There are 3 ways to arrange a number: in the first group, in the second, not used.
The number of difference will be less than
The only case to reach
The number of difference will be less than
3^N.The only case to reach
3^N is when rod = [1,3,9,27,81...]
Java, O(SN) using array, just for better reading:
public int tallestBillboard(int[] rods) {
int[] dp = new int[5001];
for (int d = 1; d < 5001; d++) dp[d] = -10000;
for (int x : rods) {
int[] cur = dp.clone();
for (int d = 0; d + x < 5001; d++) {
dp[d + x] = Math.max(dp[d + x], cur[d]);
dp[Math.abs(d - x)] = Math.max(dp[Math.abs(d - x)], cur[d] + Math.min(d, x));
}
}
return dp[0];
}
Java, using HashMap:
public int tallestBillboard(int[] rods) {
Map<Integer, Integer> dp = new HashMap<>(), cur;
dp.put(0, 0);
for (int x : rods) {
cur = new HashMap<>(dp);
for (int d : cur.keySet()) {
dp.put(d + x, Math.max(cur.get(d), dp.getOrDefault(x + d, 0)));
dp.put(Math.abs(d - x), Math.max(cur.get(d) + Math.min(d, x), dp.getOrDefault(Math.abs(d - x), 0)));
}
}
return dp.get(0);
}One Optimisation
We do the same thing for both half of
Then we try to find the same difference in both results.
rods.Then we try to find the same difference in both results.
Time Complexity:
O(NM), where we haveN = rod.length <= 20S = sum(rods) <= 5000M = all possible sum = min(3^N/2, S)
Python:
def tallestBillboard(self, rods):
def helper(A):
dp = {0: 0}
for x in A:
for d, y in dp.items():
dp[d + x] = max(dp.get(x + d, 0), y)
dp[abs(d - x)] = max(dp.get(abs(d - x), 0), y + min(d, x))
return dp
dp, dp2 = helper(rods[:len(rods) / 2]), helper(rods[len(rods) / 2:])
return max(dp[d] + dp2[d] + d for d in dp if d in dp2)X.
https://leetcode.com/problems/tallest-billboard/discuss/204232/Simplest-DP-solution-which-is-easy-to-understand
Similar to backpack DP problem as Leetcode 416. But this one is more challenging because some data point may not be chosen. Moreover, the dp definition is different.
In this question, dp[i][j] denotes the largest left sum at the case of after using i-th rod and the difference between left sum and right sum is j - sum of all rods.
Initially, I want to design dp as i-th rod and difference between left sum and right to be j, however, j could be negative, use sum of all rods to offset all negative values.
So the answer should be dp[n][sum of all rods].
In this question, dp[i][j] denotes the largest left sum at the case of after using i-th rod and the difference between left sum and right sum is j - sum of all rods.
Initially, I want to design dp as i-th rod and difference between left sum and right to be j, however, j could be negative, use sum of all rods to offset all negative values.
So the answer should be dp[n][sum of all rods].
Time complexity: O(n * sum)
Space complexity: O(n * sum)
Space complexity: O(n * sum)
public int tallestBillboard(int[] rods) {
int sum = 0;
for (int i : rods){
sum += i;
}
int n = rods.length;
int[][] dp = new int[n+1][2*sum+1];//largest sum of left at i-th rod and difference between
//sum of left and sum of right equals to j-sum
for (int i = 0; i <= n; i++){
Arrays.fill(dp[i], -1);// -1 means the value could not be reached.
}
dp[0][sum] = 0; //it means if there is no rods, the largest left sum could be 0, not -1.
for (int i = 1; i <= n; i++){
for (int j = 0; j <= 2*sum; j++){
if (j - rods[i-1] >= 0 && dp[i-1][j-rods[i-1]] != -1){//this means we will add next rod (rods[i-1] to the left,
//so the largest left sum should be added by rods[i-1] from previous step
dp[i][j] = Math.max(dp[i][j], dp[i-1][j-rods[i-1]] + rods[i-1]);
}
if (j + rods[i-1] <= 2*sum && dp[i-1][j+rods[i-1]] != -1){//this means we will add next rod(rods[i-1]) to the right,
//so largest left sum at previous step stays at dp[i-1][j+rods[i-1]]
dp[i][j] = Math.max(dp[i][j], dp[i-1][j+rods[i-1]]);
}
if (dp[i-1][j] != -1){//this means we don't use rods[i-1] but we need ensure
//previous step could be reached, so we can compare.
dp[i][j] = Math.max(dp[i][j], dp[i-1][j]);
}
}
}
return dp[n][sum];
}https://zxi.mytechroad.com/blog/dynamic-programming/leetcode-956-tallest-billboard/
如果直接暴力搜索的话时间复杂度是O(3^N),铁定超时。对于每一根我们可以选择1、放到左边,2、放到右边,3、不使用。最后再看一下左边和右边是否相同。
题目的数据规模中的这句话非常重要:
The sum of rods is at most 5000.
这句话就是告诉你算法的时间复杂度和sum of rods有关系,通常需要使用DP。
由于每根柱子只能使用一次(让我们想到了 回复 01背包),但是我们怎么去描述放到左边还是放到右边呢?
Naive的方法是用 dp[i] 表示使用前i个柱子能够构成的柱子高度的集合。
e.g. dp[i] = {(h1, h2)}, h1 <= h2
和暴力搜索比起来DP已经对状态进行了压缩,因为我并不需要关心h1, h2是通过哪些(在我之前的)柱子构成了,我只关心它们的当前高度。
然后我可以选择
1、不用第i根柱子
2、放到低的那一堆
3、放到高的那一堆
状态转移的伪代码:
for h1, h2 in dp[i – 1]:
dp[i] += (h1, h2) # not used
dp[i] += (h1, h2 + h) # put on higher
if h1 + h < h2:
dp[i] += (h1 + h, h2) # put on lower
else:
dp[i] += (h2, h1 + h) # put on lower
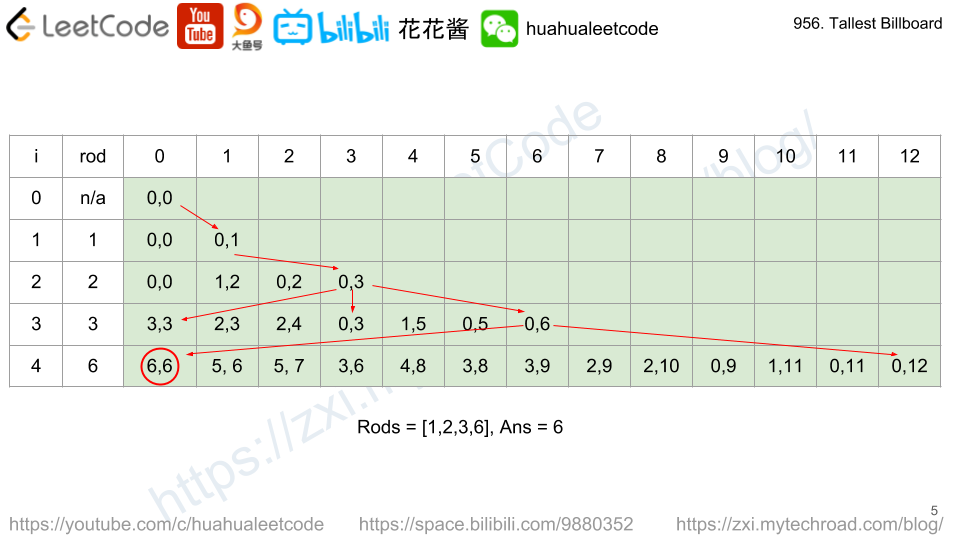
假设 rods=[1,1,2]
dp[0] = {(0,0)}
dp[1] = {(0,0), (0,1)}
dp[2] = {(0,0), (0,1), (0,2), (1,1)}
dp[3] = {(0,0), (0,1), (0,2), (0,3), (0,4), (1,1), (1,2), (1,3), (2,2)}
但是dp[i]这个集合的大小可能达到sum^2,所以还是会超时…
时间复杂度 O(n*sum^2)
空间复杂度 O(n*sum^2) 可降维至 O(sum^2)
革命尚未成功,同志仍需努力!
all pairs的cost太大,我们还需要继续压缩状态!
重点来了
通过观察发现,若有2个pairs:
(h1, h2), (h3, h4),
h1 <= h2, h3 <= h4, h1 < h3, h2 – h1 = h4 – h3 即 高度差 相同
如果 min(h1, h2) < min(h3, h4) 那么(h1, h2) 不可能产生最优解,直接舍弃。
因为如果后面的柱子可以构成 h4 – h3/h2 – h1 填补高度差,使得两根柱子一样高,那么答案就是 h2 和 h4。但h2 < h4,所以最优解只能来自后者。
举个例子:我有 (1, 3) 和 (2, 4) 两个pairs,它们的高度差都是2,假设我还有一个长度为2的柱子,那么我可以构成(1+2, 3) 以及 (2+2, 4),虽然这两个都是解。但是后者的高度要大于前者,所以前者无法构成最优解,也就没必要存下来。
所以,我们可以把状态压缩到高度差,对于相同的高度差,我只存h1最大的。
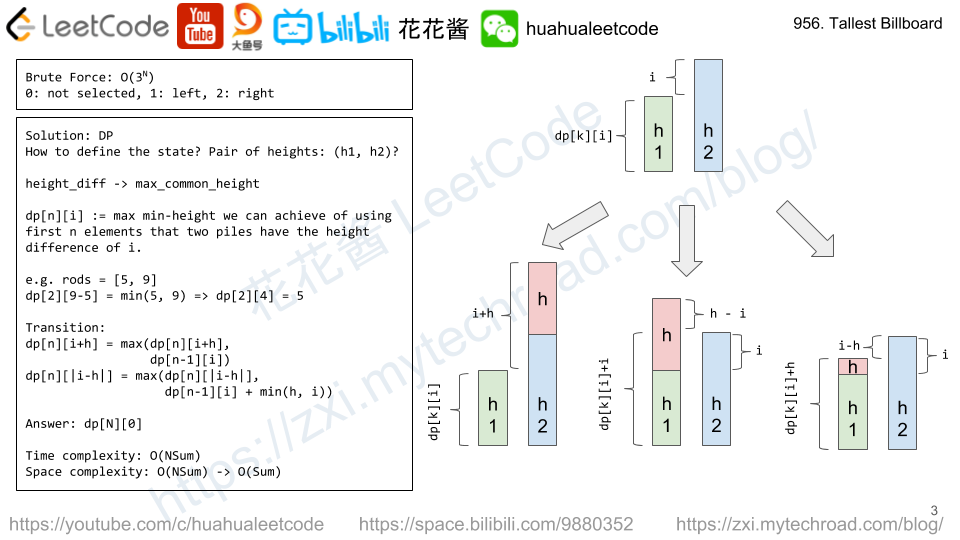
我们用 dp[i][j] 来表示使用前i个柱子,高度差为j的情况下最大的公共高度h1是多少。
状态转移(如下图)
dp[i][j] = max(dp[i][j], dp[i – 1][j])
dp[i][j+h] = max(dp[i][j + h], dp[i – 1][j])
dp[i][|j-h|] = max(dp[i][|j-h|], dp[i – 1][j] + min(j, h))
时间复杂度 O(nsum)
空间复杂度 O(nsum) 可降维至 O(sum)
dp[i] := max common height of two piles of height difference i.
e.g. y1 = 5, y2 = 9 => dp[9 – 5] = min(5, 9) => dp[4] = 5.
answer: dp[0]
Time complexity: O(n*Sum)
Space complexity: O(Sum)
int tallestBillboard(vector<int>& rods) {
unordered_map<int, int> dp;
dp[0] = 0;
for (int rod : rods) {
auto cur = dp;
for (const auto& kv : cur) {
const int k = kv.first;
dp[k + rod] = max(dp[k + rod], cur[k]);
dp[abs(k - rod)] = max(dp[abs(k - rod)], cur[k] + min(rod, k));
}
}
return dp[0];
}
https://www.acwing.com/solution/LeetCode/content/644/
状态 f(i,j)f(i,j) 表示考虑了前 ii 个钢筋,搭建的两个钢制支架差距为 jj 时,较低的支架 的最大高度是多少。
初始化 f(i,j)=−∞f(i,j)=−∞,f(0,0)=0f(0,0)=0。
转移时,如果不用第 ii 个钢筋,则 f(i,j)=max(f(i,j),f(i−1,j))f(i,j)=max(f(i,j),f(i−1,j));如果使用了第 ii 个钢筋,并将它放到了较高的支架上,则差距会扩大 rods[i],即 f(i,j+x)=max(f(i,j+x),f(i−1,j))f(i,j+x)=max(f(i,j+x),f(i−1,j));若放到了较低的支架上,并且差距 jj 小于等于 rods[i],则 f(i,j−x)=max(f(i,j−x),f(i−1,j)+x)f(i,j−x)=max(f(i,j−x),f(i−1,j)+x),否则 f(i,x−j)=max(f(i,x−j),f(i−1,j)+j)f(i,x−j)=max(f(i,x−j),f(i−1,j)+j)。
最终答案为 f(n,0)f(n,0)。
int tallestBillboard(vector<int>& rods) {
int n = rods.size(), sum = 0;
vector<vector<int>> f(n + 1, vector<int>(5010, -5010));
f[0][0] = 0;
for (int i = 1; i <= n; i++) {
sum += rods[i - 1];
for (int j = 0; j <= sum; j++) {
f[i][j] = max(f[i][j], f[i - 1][j]);
int x = rods[i - 1];
if (j + x <= sum)
f[i][j + x] = max(f[i][j + x], f[i - 1][j]);
if (x <= j)
f[i][j - x] = max(f[i][j - x], f[i - 1][j] + x);
else
f[i][x - j] = max(f[i][x - j], f[i - 1][j] + j);
}
}
return f[n][0];
}
把这个问题看成是扩展版的01背包问题:对于每根棍子,我们可以把它加入背包中,不加入背包中,还可以把它从背包中减去。
令
X. DFS + cachef[i][j]表示用前i根棍子能否组成和为j的长度(j有可能是负的)。则f[i+1][j] = f[i][j] || f[i][j-rods[i+1]] || f[i][j+rods[i+1]]。为了找到可能的最大长度,用辅助数组g[i][j]记录f[i][j]为真时,最大可能的正长度之和。算法的复杂度为O(10000*N)
I know it's not as cool as a DP solution, though during the context it may be quicker to do DFS and add memoisation if you get TLE.
So we go through all rods, and either skip the rod, add it to the first support (
s1), or to the second support (s2). The result is the maximum of these three operations. When we exhausted all rods (i >= rs.size()), we return the rod size if both rods are the same, or zero. This way, our simple DFS solution can be implemented in just a few lines of code:int tallestBillboard(vector<int>& rods, int i = 0, int s1 = 0, int s2 = 0) {
if (i >= rods.size()) return s1 == s2 ? s1 : 0;
return max({ tallestBillboard(rods, i + 1, s1, s2),
tallestBillboard(rods, i + 1, s1 + rods[i], s2),
tallestBillboard(rods, i + 1, s1, s2 + rods[i]) });
}
You'll probably get TLE (certainly, in this particular case) for a simple DFS solution, so the next step is to think about memoisation to avoid processing identical conditions over and over again. We could memoise support sizes
s1 and s2 for the current rod number i. However, that would require a lot of memory (and we will get MLE or TLE).
The intuition here is that we do not need to memoise the actual support sizes; all is what it's important is the delta:
abs(s1 - s2). For example, if for i rod, first support is s1 == 50, the second is s2 == 30, and in the final suport sizes matches and equals 200, we will record m[i][50 - 30] = 200 - 50 or m[i][20] = 150. Next time we process i and support sizes are 100 and 80 (the delta is 20), we know that there are matched size in the end that adds 150 to the larger support: m[i][100 - 80] + max(100, 80) = m[i][20] + 100 = 150 + 100 = 250.int dfs(vector<int>& rs, int i, int s1, int s2, int m_sum, vector<vector<int>> &m) {
if (s1 > m_sum || s2 > m_sum) return -1;
if (i >= rs.size()) return s1 == s2 ? s1 : -1;
if (m[i][abs(s1 - s2)] == -2) {
m[i][abs(s1 - s2)] = max(-1, max({ dfs(rs, i + 1, s1, s2, m_sum, m),
dfs(rs, i + 1, s1 + rs[i], s2, m_sum, m), dfs(rs, i + 1, s1, s2 + rs[i], m_sum, m) }) - max(s1, s2));
}
return m[i][abs(s1 - s2)] + (m[i][abs(s1 - s2)] == -1 ? 0 : max(s1, s2));
}
int tallestBillboard(vector<int>& rods) {
int m_sum = accumulate(begin(rods), end(rods), 0) / 2;
vector<vector<int>> m(rods.size(), vector<int>(m_sum + 1, -2));
return max(0, dfs(rods, 0, 0, 0, m_sum, m));
}
As an additinal optimization, I am also calculating maximum possible billboard (sum of all rods divide by 2), and using it for pruning and vector allocation. As the result, this solution runtime beats most of DP solutions other folks posted
X.
https://leetcode.com/articles/tallest-billboard/
Typically, the complexity of brute force can be reduced with a "meet in the middle" technique. As applied to this problem, we have possible states, from writing either
+x, -x, or 0 for each rod x, and we want to make this brute force faster.
What we can do is write the first and last states separately, and attempt to combine them. For example, if we have rods
[1, 3, 5, 7], then the first two rods create up to nine states: [0+0, 0+3, 0-3, 1+0, 1+3, 1-3, -1+0, -1+3, -1-3], and the last two rods also create nine states.
We will store each state as the sum of positive terms, and the sum of absolute values of the negative terms. For example,
+1 +2 -3 -4 becomes (3, 7). Let's also call the difference 3 - 7 to be the delta of this state, so this state has a delta of -4.
Our high level goal is to combine states with deltas that sum to
0. The score of a state will be the sum of the positive terms, and we want the highest score. Note that for each delta, we only care about the state that has the highest score.
Algorithm
Split the rods into two halves: left and right.
For each half, use brute force to compute the reachable states as defined above. Then, for each state, record the delta and the maximum score.
Now, we have a left and right halves with
[(delta, score)] information. We'll find the largest total score, with total delta 0.
public int tallestBillboard(int[] rods) {
int N = rods.length;
Map<Integer, Integer> Ldelta = make(Arrays.copyOfRange(rods, 0, N / 2));
Map<Integer, Integer> Rdelta = make(Arrays.copyOfRange(rods, N / 2, N));
int ans = 0;
for (int d : Ldelta.keySet())
if (Rdelta.containsKey(-d))
ans = Math.max(ans, Ldelta.get(d) + Rdelta.get(-d));
return ans;
}
public Map<Integer, Integer> make(int[] A) {
Point[] dp = new Point[60000];
int t = 0;
dp[t++] = new Point(0, 0);
for (int v : A) {
int stop = t;
for (int i = 0; i < stop; ++i) {
Point p = dp[i];
dp[t++] = new Point(p.x + v, p.y);
dp[t++] = new Point(p.x, p.y + v);
}
}
Map<Integer, Integer> ans = new HashMap();
for (int i = 0; i < t; ++i) {
int a = dp[i].x;
int b = dp[i].y;
ans.put(a - b, Math.max(ans.getOrDefault(a - b, 0), a));
}
return ans;
}
解法2:中间相遇法
把
rods数组分成大致相等的两半,然后对每一半都枚举每根棍子是+,-还是0。然后对于左边的一半得到的和,在右边寻找这个和的负值是否存在。最后取最大值。算法复杂度为O(3^(N/2))。
这个算法也需要记录最大可能的正长度之和
unordered_map<int, int> results; // 和 - 最大正值和 int M, N; int ans; // 枚举棍子状态:sum是和,p是正值和 void dfs(int x, int sum, int p, vector<int>& rods, bool check) { if (x >= rods.size()) { if (!check) results[sum] = max(results[sum], p); else { if (results.find(-sum) != results.end()) ans = max(ans, results[-sum] + p); } return; } dfs(x+1, sum, p, rods, check); dfs(x+1, sum+rods[x], p+rods[x], rods, check); dfs(x+1, sum-rods[x], p, rods, check); } public: int tallestBillboard(vector<int>& rods) { N = rods.size(); if (N == 0) return 0; M = N / 2; vector<int> rod1, rod2; for (int i = 0; i < M; i++) rod1.push_back(rods[i]); for (int i = M; i < N; i++) rod2.push_back(rods[i]); ans = 0; dfs(0, 0, 0, rod1, false); dfs(0, 0, 0, rod2, true); return ans; }
https://blog.csdn.net/xx_123_1_rj/article/details/86557102