https://leetcode.com/problems/shortest-path-visiting-all-nodes/
https://blog.csdn.net/fuxuemingzhu/article/details/82939203
话说看到这个题的第一感觉就是BFS,因为我们要找到遍历所有节点的最少步数,这个正是BFS擅长的。唯一不同的就是这个题允许从多个顶点出发,也就是说没有了固定的起点。那么需要对BFS稍微改变一点,即在初始化的时候,把所有顶点都放进队列之中,这样,每次把队列的元素pop出来一遍之后就是新的一轮循环,也就可以认为所有的节点都是同时向前迈进了一步。
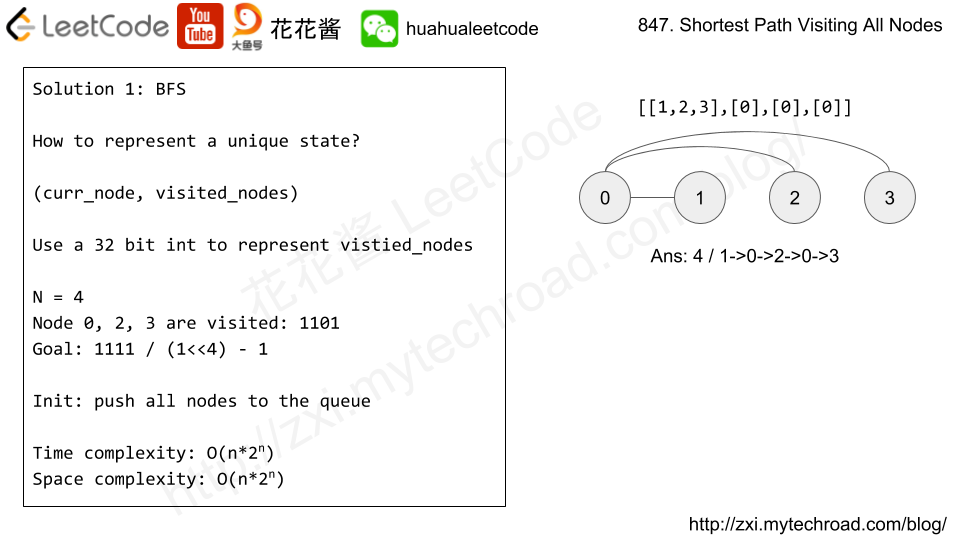
这个题使用了一个的技巧,位运算。一般的BFS过程都是只保存访问过的节点即可,因为每个节点只可以使用一次,但是这个题的节点可以访问多次,那么就是说必须维护一个实时的访问了哪些节点的状态。按道理说,如果不使用位运算而是使用字典等方式保存访问过了的状态也可以,但是,看了给出的图的顶点个数只有12个,哪怕一个int都会有32个bit够用,所以可以直接使用和图中顶点数相等的位数来保存这个状态是否访问过。这个状态怎么理解?从每个顶点出发到达,所有访问过的节点是状态。也就是说这个状态是全局唯一的,每个顶点都有2 * N个状态表示它访问的其他节点。有2 ^ N个bit,每个位都代表对应的节点是否访问过。最终的状态是(1 << N) - 1,即全是1,表示所有节点都访问了。
这个visited是个二维数组,保存的是每个节点的所有状态,对于该题目的BFS,有可能有N * 2^N个状态,使用visited保存每个节点已经访问的状态,对应状态位置是0/1。
时间复杂度是O(N * (2^N)),空间复杂度是O(N * 2^N)。
https://tinacristal.github.io/2018/12/07/shor/
https://leetcode.com/problems/shortest-path-visiting-all-nodes/discuss/135809/Fast-BFS-Solution-(46ms)-Clear-Detailed-Explanation-Included
we could get rid of the cost attribute just by looping the queue by levels. It will cause less confusion. See
https://leetcode.com/articles/shortest-path-visiting-all-nodes/
Approach #1: Breadth First Search [Accepted]
Approach #2: Dynamic Programming [Accepted]
http://bookshadow.com/weblog/2018/06/03/leetcode-shortest-path-visiting-all-nodes/
An undirected, connected graph of N nodes (labeled
0, 1, 2, ..., N-1) is given as graph.graph.length = N, and j != i is in the list graph[i] exactly once, if and only if nodes i and j are connected.
Return the length of the shortest path that visits every node. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.
Example 1:
Input: [[1,2,3],[0],[0],[0]] Output: 4 Explanation: One possible path is [1,0,2,0,3]
Example 2:
Input: [[1],[0,2,4],[1,3,4],[2],[1,2]] Output: 4 Explanation: One possible path is [0,1,4,2,3]
Note:
1 <= graph.length <= 120 <= graph[i].length < graph.length
https://blog.csdn.net/fuxuemingzhu/article/details/82939203
话说看到这个题的第一感觉就是BFS,因为我们要找到遍历所有节点的最少步数,这个正是BFS擅长的。唯一不同的就是这个题允许从多个顶点出发,也就是说没有了固定的起点。那么需要对BFS稍微改变一点,即在初始化的时候,把所有顶点都放进队列之中,这样,每次把队列的元素pop出来一遍之后就是新的一轮循环,也就可以认为所有的节点都是同时向前迈进了一步。
这个题使用了一个的技巧,位运算。一般的BFS过程都是只保存访问过的节点即可,因为每个节点只可以使用一次,但是这个题的节点可以访问多次,那么就是说必须维护一个实时的访问了哪些节点的状态。按道理说,如果不使用位运算而是使用字典等方式保存访问过了的状态也可以,但是,看了给出的图的顶点个数只有12个,哪怕一个int都会有32个bit够用,所以可以直接使用和图中顶点数相等的位数来保存这个状态是否访问过。这个状态怎么理解?从每个顶点出发到达,所有访问过的节点是状态。也就是说这个状态是全局唯一的,每个顶点都有2 * N个状态表示它访问的其他节点。有2 ^ N个bit,每个位都代表对应的节点是否访问过。最终的状态是(1 << N) - 1,即全是1,表示所有节点都访问了。
这个visited是个二维数组,保存的是每个节点的所有状态,对于该题目的BFS,有可能有N * 2^N个状态,使用visited保存每个节点已经访问的状态,对应状态位置是0/1。
时间复杂度是O(N * (2^N)),空间复杂度是O(N * 2^N)。
https://tinacristal.github.io/2018/12/07/shor/
用二进制的数来表示当前访问节点的状态
4个节点 如1101表示 0,2,3号节点已访问过
4个节点 如1101表示 0,2,3号节点已访问过
最后的终止状态是1111
或者用Hashtable 也可以
为了遍历所有的节点 一个节点可以被重复访问 所以不能用 vis[cur] 跳过访问过的节点
但是不跳过访问过的状态 可能会陷入 0->1->0的死循环
所以建立二维数组vis 记录当前访问过的节点和状态
不会重复在这个节点的访问状态
即 在1号节点已经访问过0号,1号房间
不会重复在这个节点的访问状态
即 在1号节点已经访问过0号,1号房间
pair<int,int> {1,0011}
即在搜索1号节点的邻居时不会再访问0号节点 因为此时状态不会更新
还是 0011
https://github.com/cherryljr/LeetCode/blob/master/Shortest%20Path%20Visiting%20All%20Nodes.java还是 0011
* 题目要求走遍所有点的最短路径(最少步数)。而该图是一个 权值为1的无向图。
* 并且数据规模为 node <= 12, 所以首先可以考虑使用 BFS 来做。
*
* 该题与平时遇到的 BFS 不同点在于,在同一条路径(同一轮遍历)中,一个点是可以被重复遍历的。
* 而我们平时都是会记录一个 visited 数组来避免遍历重复的点,或者是限制加入队列的条件
* 来减小问题的规模。否则就会出现死循环。而这也是本题的难点所在。
*
* 对此我们仍然可以通过记录 visited 状态来解决。
* 只不过这里需要记录的状态为:当前的位置 以及 对应的遍历过的节点状态
* 当我们从一个节点出发,遍历后没有新的节点增加的话,那就说明我们走的路是无用的。
* 同时因为节点个数最多只有 12 个,所以我们可以通过 二进制 来表示状态从而达到优化的效果。
*
* 注:这里使用了 进队列 时进行判断的做法,代码上看上去可能没那么好看(for循环遍历邻居时)
* 但是在时间上可以优化不少。
* 关于这点的分析可以详细参考:
* https://github.com/cherryljr/LintCode/blob/master/Matrix%20Water%20Injection.java
public int shortestPathLength(int[][] graph) {
int n = graph.length;
// 采用 入队列时判断 的BFS做法,因此需要处理一下起始情况。
if (n <= 1) {
return 0;
}
Queue<int[]> queue = new LinkedList<>();
boolean[][] visited = new boolean[n][1 << n];
// 可以选择任意点作为起点,因此开始时需要将所有的节点都 add 到队列中
for (int i = 0; i < n; i++) {
queue.offer(new int[]{i, 1 << i});
visited[i][1 << i] = true;
}
// 采用二进制记录状态信息
int target = (1 << n) - 1;
int step = 0;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
int[] curr = queue.poll();
int pos = curr[0], state = curr[1];
for (int neigh : graph[pos]) {
int nextState = state | (1 << neigh);
if (nextState == target) {
return step + 1;
}
if (visited[neigh][nextState]) {
continue;
}
visited[neigh][nextState] = true;
queue.offer(new int[]{neigh, state | (1 << neigh)});
}
}
step++;
}
return -1;
}
https://leetcode.com/problems/shortest-path-visiting-all-nodes/discuss/135686/Java-DP-Solutionhttps://leetcode.com/problems/shortest-path-visiting-all-nodes/discuss/135809/Fast-BFS-Solution-(46ms)-Clear-Detailed-Explanation-Included
we could get rid of the cost attribute just by looping the queue by levels. It will cause less confusion. See
https://leetcode.com/articles/shortest-path-visiting-all-nodes/
Approach #1: Breadth First Search [Accepted]
A path 'state' can be represented as the subset of nodes visited, plus the current 'head' node. Then, the problem reduces to a shortest path problem among these states, which can be solved with a breadth-first search.
Let's call the set of nodes visited by a path so far the cover, and the current node as the head. We'll store the
cover states using set bits: k is in the cover if the kth bit of cover is 1.
For states
state = (cover, head), we can perform a breadth-first search on these states. The neighbors are (cover | (1 << child), child) for each child in graph[head].
If at any point we find a state with all set bits in it's cover, because it is a breadth-first search, we know this must represent the shortest path length.
- Time Complexity: .
- Space Complexity: .
public int shortestPathLength(int[][] graph) {
int N = graph.length;
Queue<State> queue = new LinkedList<>();
int[][] dist = new int[1 << N][N];
for (int[] row : dist)
Arrays.fill(row, N * N);
for (int x = 0; x < N; ++x) {
queue.offer(new State(1 << x, x));
dist[1 << x][x] = 0;
}
while (!queue.isEmpty()) {
State node = queue.poll();
int d = dist[node.cover][node.head];
if (node.cover == (1 << N) - 1)
return d;
for (int child : graph[node.head]) {
int cover2 = node.cover | (1 << child);
if (d + 1 < dist[cover2][child]) {
dist[cover2][child] = d + 1;
queue.offer(new State(cover2, child));
}
}
}
throw null;
}
class State {
int cover, head;
State(int c, int h) {
cover = c;
head = h;
}
}
Approach #2: Dynamic Programming [Accepted]
http://bookshadow.com/weblog/2018/06/03/leetcode-shortest-path-visiting-all-nodes/
Floyd + 动态规划(Dynamic Programming)
时间复杂度 O(2^n * n^2)
A path 'state' can be represented as the subset of nodes visited, plus the current 'head' node. As in Approach #1, we have a recurrence in states:
answer(cover, head) is min(1 + answer(cover | (1<<child), child) for child in graph[head]). Because these states form a DAG (a directed graph with no cycles), we can do dynamic programming.
Algorithm
Let's call the set of nodes visited by a path so far the cover, and the current node as the head. We'll store
dist[cover][head] as the length of the shortest path with that cover and head. We'll store the coverstates using set bits, and maintain the loop invariant (on cover), that dist[k][...] is correct for k < cover.
For every state
(cover, head), the possible next (neighbor) nodes in the path are found in graph[head]. The new cover2 is the old cover plus next.
For each of these, we perform a "relaxation step" (for those familiar with the Bellman-Ford algorithm), where if the new candidate distance for
dist[cover2][next] is larger than dist[cover][head] + 1, we'll update it to dist[cover][head] + 1.
Care must be taken to perform the relaxation step multiple times on the same cover if
cover = cover2. This is because a minimum state for dist[cover][head] might only be achieved through multiple steps through some path.
Finally, it should be noted that we are using implicitly the fact that when iterating
cover = 0 .. (1<<N) - 1, that each new cover cover2 = cover | 1 << x is such that cover2 >= cover. This implies a topological ordering, which means that the recurrence on these states form a DAG.- Time Complexity: .
- Space Complexity: .
public int shortestPathLength(int[][] graph) {
int N = graph.length;
int dist[][] = new int[1 << N][N];
for (int[] row : dist)
Arrays.fill(row, N * N);
for (int x = 0; x < N; ++x)
dist[1 << x][x] = 0;
for (int cover = 0; cover < 1 << N; ++cover) {
boolean repeat = true;
while (repeat) {
repeat = false;
for (int head = 0; head < N; ++head) {
int d = dist[cover][head];
for (int next : graph[head]) {
int cover2 = cover | (1 << next);
if (d + 1 < dist[cover2][next]) {
dist[cover2][next] = d + 1;
if (cover == cover2)
repeat = true;
}
}
}
}
}
int ans = N * N;
for (int cand : dist[(1 << N) - 1])
ans = Math.min(cand, ans);
return ans;
}