Massive Algorithms: LeetCode 1000 - Minimum Cost to Merge Stones

LeetCode 1000 - Minimum Cost to Merge Stones

Related:
Burst Balloons
Remove Boxes
Cherry Pickup
https://leetcode.com/problems/minimum-cost-to-merge-stones/

There are N piles of stones arranged in a row. The i-th pile has stones[i] stones.

A move consists of merging exactly K consecutive piles into one pile, and the cost of this move is equal to the total number of stones in these K piles.

Find the minimum cost to merge all piles of stones into one pile. If it is impossible, return -1.

Example 1:

Input: stones = [3,2,4,1], K = 2
Output: 20
Explanation: 
We start with [3, 2, 4, 1].
We merge [3, 2] for a cost of 5, and we are left with [5, 4, 1].
We merge [4, 1] for a cost of 5, and we are left with [5, 5].
We merge [5, 5] for a cost of 10, and we are left with [10].
The total cost was 20, and this is the minimum possible.

Example 2:

Input: stones = [3,2,4,1], K = 3
Output: -1
Explanation: After any merge operation, there are 2 piles left, and we can't merge anymore.  So the task is impossible.

Example 3:

Input: stones = [3,5,1,2,6], K = 3
Output: 25
Explanation: 
We start with [3, 5, 1, 2, 6].
We merge [5, 1, 2] for a cost of 8, and we are left with [3, 8, 6].
We merge [3, 8, 6] for a cost of 17, and we are left with [17].
The total cost was 25, and this is the minimum possible.

Note:

1 <= stones.length <= 30
2 <= K <= 30
1 <= stones[i] <= 100

https://zxi.mytechroad.com/blog/dynamic-programming/leetcode-1000-minimum-cost-to-merge-stones/

dp[i][j][k] := min cost to merge subarray i ~ j into k piles
Init: dp[i][j][k] = 0 if i==j and k == 1 else inf
ans: dp[0][n-1][1]
transition:
1. dp[i][j][k] = min{dp[i][m][1] + dp[m+1][j][k-1]} for all i <= m < j
2. dp[i][j][1] = dp[i][j][K] + sum(A[i]~A[j])

Time complexity: O(n^3)
Space complexity: O(n^2*K)

  int mergeStones(vector<int>& stones, int K) {

    const int n = stones.size();

    if ((n - 1) % (K - 1)) return -1;

    const int kInf = 1e9;    

    vector<int> sums(n + 1);

    for (int i = 0; i < stones.size(); ++i)

      sums[i + 1] = sums[i] + stones[i];

    // dp[i][j][k] := min cost to merge subarray i~j into k piles.

    vector<vector<vector<int>>> dp(n, vector<vector<int>>(n, vector<int>(K + 1, kInf)));

    for (int i = 0; i < n; ++i)

      dp[i][i][1] = 0;

    for (int l = 2; l <= n; ++l) // subproblem length

      for (int i = 0; i <= n - l; ++i) { // start

        int j = i + l - 1; // end

        for (int k = 2; k <= K; ++k) // piles

          for (int m = i; m < j; m += K - 1) // split point

            dp[i][j][k] = min(dp[i][j][k], dp[i][m][1] + dp[m + 1][j][k - 1]);

        dp[i][j][1] = dp[i][j][K] + sums[j + 1] - sums[i];

}

    return dp[0][n - 1][1];

}

http://www.noteanddata.com/leetcode-1000-Minimum-Cost-to-Merge-Stones-java-solution-note.html

先考虑几个特殊情况，
a. 如果正好有K个石头，那么，自然可以合并成一堆，然后总成本就是所有石头的重量和
b. 如果正好有K+1个石头，那么，第一步只有两种操作可能，一种是先把前面的K个合并成一个，另外一种是先把后面的K个合并成一个
这时候，如果K=2，那么，可以继续合并成一堆。如果K > 2 , 那么，就无法合并了。
c. 如果有K+2个石头，第一步只有三种操作可能， [0,K), [1,K+1), [2,K+2), 然后，合并完以后，还剩下三个石头，如果K=3, 那么，可以合并成一个石头，否则，就不能合并。
从上面的特殊情况可以看到，
a. 无论如何操作，如果最后可以合并，最后一步，一定是把K个石头合并成一个，然后最后的成本都是固定的。
b. 这里，我当时在做题的时候陷入了错误的方向，我考虑在n个位置里面做组合选k-1个位置出来, 这样可以把n个数分成k个，
然后再递归+memorization，然后马上就陷入充满荆棘的错误道路。
c. 实际上，进一步思考一下，最后一步有k堆，
但是状态可以定义成三维数组， dp[i][j][c]表示从i到j的数组，然后有c个石头的最小成本, 其中c<=k,
这样，做k个石头的merge的时候，可以不用选择k-1个位置，而直接选择一个位置，这个位置后面是1个石头，这个位置前面是k-1个石头，
这样，就可以通过在空间上升一维（二维变三维)，从而把时间复杂度大大降低。
遇到一个problem(i,j,c)的时候，可以直接对i和j之间的每个位置做循环，把前面的分成c-1个，后面分成1个，
d. 这样，普通成本的递推关系就是dp[i][j][c] = dp[i][t][c-1] + dp[t+1][j][1]
如果是求dp[i][j][1] = dp[i][j][k] + sum[i][j]
e. 上面两个公式略有点奇怪，因为通常的dp公式都是一个公式解决所有的递推关系的，
其中dp[i][j][1] = dp[i][j]k] + sum[i][j]非常好理解，这就是做一个merge的操作
而另外一个公式， dp[i][j][c] = dp[i][t][c-1] + dp[t+1][j][1]，这里的含义其实是指寻找切分，并没有做merge的操作。
f. 这里可能会有个问题，为什么不直接merge了呢？比如直接定义dp[i][j][k] = dp[i][t][k-1] + dp[t+1][j][1] + sum[i][j]?
这是因为虽然对k可以这样定义，但是k-1的时候就不能这样定义了。因为我们merge只发生在k的时候，所以，定义成切分会比较合理，
假设k=3， dp[i][j][3] = dp[i][t][2] + dp[t+1][j][1]
dp[i][j][2] = dp[i][t][1] + dp[t+1][j][1]
定义成切分，那就比较容易理解，左边分成两个石头的情况就是一个石头+一个石头的情况。
h. 边界条件，主要就是i=j的情况，
dp[i][i][1] = 0 // 一个石头分一堆，不需要任何成本
dp[i][i][x] = invalid // if x > 1, 一个石头分成多堆是不可能的

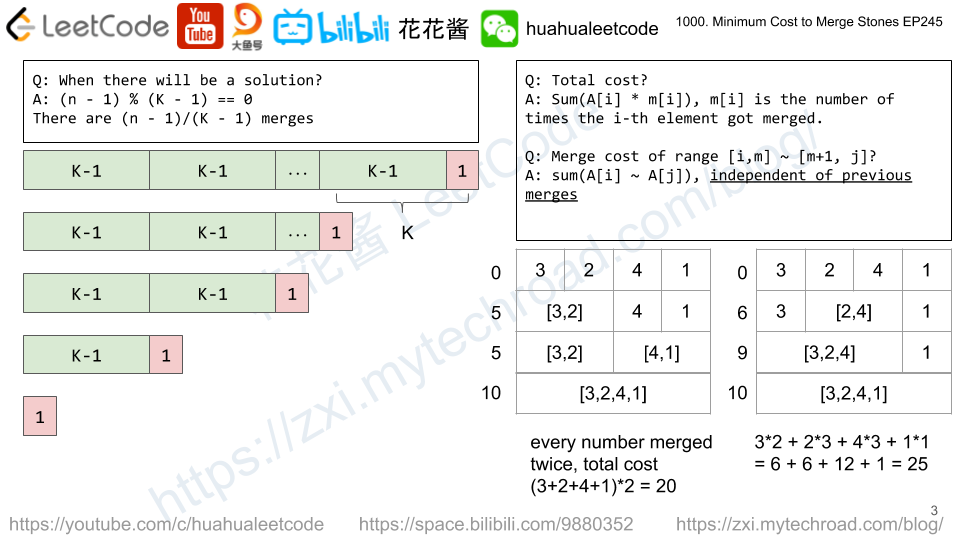
http://www.cnblogs.com/grandyang/p/10493371.html

这道题给了我们N堆石头，每堆石头有不同的个数，说每次可以合并K堆石头，合并堆的花费就是石头的个数，然后问如何合并，才能使总花费最小。然后给了一些例子，通过观察例子，我们可以发现，并不是所有的输入都能成功合成一堆，比如例子2，无论先和并哪三堆，最终都会剩下两堆，从而无法进一步合并，因为 K=3，每次至少需要合并三堆。我们当然希望能在开始合并之前就能知道最终是否能成功合并为一堆，而不是算到最后了才发现白忙了一场，所以我们要来分析一下，什么时候才能最终合并为一堆。再来看看例子2，每次要将三堆合并为一堆，那么就是减少了两堆，而要使得最终能够剩下一堆，其他的都要合并调，那么假设原来共有n堆，只能剩下一堆，就是说 n-1 堆都要减掉，而每次只能减少 k-1 堆，所以只要 n-1 能够整除 k-1即可，即 (n-1)%(k-1) == 0 成立，这样我们就可以提前判断了。

好，接下来继续，考虑如何来解题，首先要意识到这道题的情况可能非常多，用暴力搜索的话可能会非常的复杂，而且当前的合并方法完全会影响到之后的合并，所以基本是要放弃Brute force的想法的。同样，这道题也不能用贪婪算法，每次都合并石子个数最少的三堆会收敛到局部峰值，不一定是全局的，所以只能另辟蹊径。观察到这题是玩数组的，又是求极值的题目，那么就要祭出神器动态规划Dynamic Programming了，那么先来考虑定义dp数组吧，那么最简单直接的方法肯定直接用个二维的dp数组了，其中 dp[i][j] 表示合并范围 [i, j] 内的石头堆的最小花费，那么最终 dp[0][n-1] 就是所要求的值。看到了论坛上有人定义了三维的dp数组，把每次合并的堆数K也当作一维放入到dp数组中了，其实博主觉得不是很有必要，因为像这种必须要对dp数组进行升维操作的是当题目中有隐藏信息Hidden Information，而当前定义的dp数组无法重现子问题，即无法找到状态转移方程的时候必须要做的，最典型的例子就是之前那道 Remove Boxes，那道题自区间的dp值非常依赖于区间左边相同的数字的个数，而这道题每次合并的堆数K并不是很依赖其他小于K的合并的堆数，所以博主感觉没有必要加。关于含有隐藏信息的dp题目，博主感觉巅峰就属于拣樱桃那题 Cherry Pickup 了吧，现在看还是有点晕，改天还得重新加工一下吧。其实跟这道题最像的当属于打气球那题 Burst Balloons，气球爆了之后，两边的气球就挨到一起了，这里也很类似，石子合并之后，再跟两边的石子堆继续合并，这里的更新方式还是从小区间更新到大区间，跟打气球那题的思路非常的相似，建议先去看看博主的之前那篇博客 Burst Balloons，会对理解这道题大有裨益。

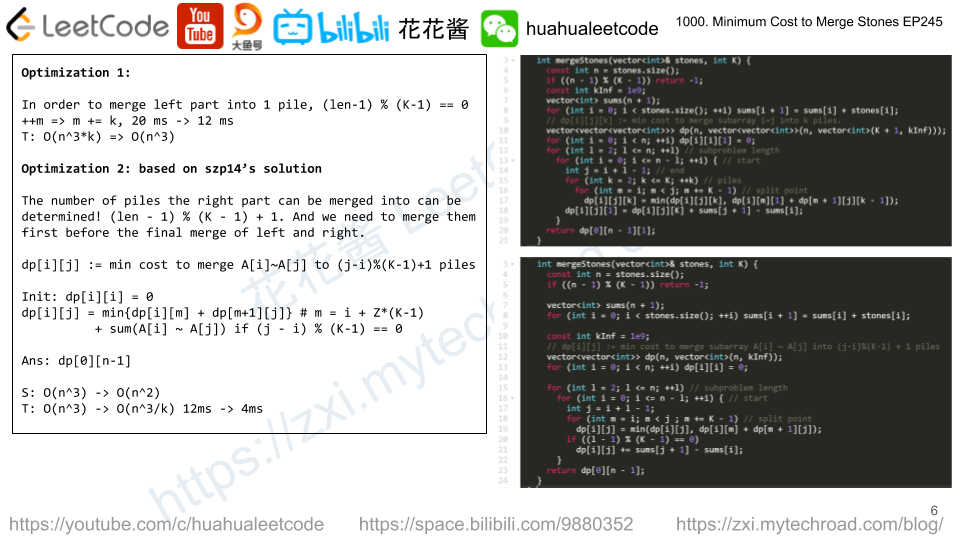
根据之前打气球的经验，我们要从小区间开始更新，多小呢，从K开始，因为小于K的区间不用更新，其dp值一定为0，因为每次必须合并K堆石子，所以区间的长度 len 从 K 遍历到 n。好，区间长度确定了，现在要确定起点了，i从 0 遍历到 n-len即可，有了区间的起点和长度，可以确定区间的终点 j = i+len-1。我们的目标就是要更新区间 [i, j] 的dp值，先初始化为整型最大值。接下来的更新方法，即状态转移方程，就是本题最大的难点了，要求区间 [i, j] 的dp值，没法直接得到，但是由于我们是从小区间开始更新的，所以suppose其中的小区间的dp值，我们都已经更新好了，那么我们就可以将大区间拆成两个小区间来更新了。一般来讲，我们将一个数组拆成两个非空子数组的时候，会遍历其所有情况，比如 [1, 2, 3, 4]，会拆成 [1]和[2,3,4]，[1,2]和[3,4], [1,2,3]和[4]。但是这道题由于其特殊性，并不需要遍历所有的拆分情况，因为某些区间是无法通过合并石子堆得到的，就拿上面的例子来说，若 K=3，那么就不需要用[1,2]和[3,4]来更新整个区间，它们都不到3个，无法合并，所以我们遍历的时候每次跳过 K-1 个位置即可，用 t 来分别区间 [i, j]，然后每次 t += K-1即可，用两个小区间的dp值来更新整个区间。这还没有完，当某个子区间正好可以合并为一堆石子的时候，其dp值要加上该区间所有的石子数。举个最简单的例子，比如 [1, 2, 3]，K=3，那么我们分割的话，只能用 dp[0][0] + dp[1][2] 来更新 dp[0][1]，但是 dp[0][0] 和 dp[1][2] 均为0，因为区间长度均小于3，那么我们的 dp[0][2] 值就无法更新成正确的值了，这三个数字是可以合并的，所以我们要加上区间内所有的数字之和，而为了快速的求得任意区间和，我们采用提前建立累加和数组sums的方式，来提高计算效率，所以整个状态转移方程为：

dp[i][j] = min(dp[i][j], dp[i][t] + dp[t + 1][j]); -> (i <= t < j)

dp[i][j] += sums[j + 1] - sums[i]; -> if ((j - i) % (K - 1) == 0)

int mergeStones(vector<int>& stones, int K) { int n = stones.size(); if ((n - 1) % (K - 1) != 0) return -1; vector<int> sums(n + 1); vector<vector<int>> dp(n, vector<int>(n)); for (int i = 1; i < n + 1; ++i) { sums[i] = sums[i - 1] + stones[i - 1]; } for (int len = K; len <= n; ++len) { for (int i = 0; i + len <= n; ++i) { int j = i + len - 1; dp[i][j] = INT_MAX; for (int t = i; t < j; t += K - 1) { dp[i][j] = min(dp[i][j], dp[i][t] + dp[t + 1][j]); } if ((j - i) % (K - 1) == 0) { dp[i][j] += sums[j + 1] - sums[i]; } } } return dp[0][n - 1]; }

https://leetcode.com/problems/minimum-cost-to-merge-stones/discuss/247567/Python-Top-Down-DP-52ms

dp[i][j][m] means the cost needed to merge stone[i] ~ stones[j] into m piles.

Initial status dp[i][i][1] = 0 and dp[i][i][m] = infinity

dp[i][j][m] = min(dp[i][mid][1] + dp[mid + 1][j][m - 1] + stonesNumber[i][j])

    Integer[][][] memo;
    int[] preSum;

    public int mergeStones(int[] stones, int K) {
        if (stones == null || stones.length == 0) return -1;

        int n = stones.length;
        if (n == 1) return 0;
        preSum = new int[n + 1];
        for (int i = 0; i < n; i++) {
            preSum[i + 1] = preSum[i] + stones[i];
        }

        if (n == K) {
            return preSum[n];
        }

        if ((n - 1) % (K - 1) != 0) return -1;

        memo = new Integer[n][n][K + 1];
        for (int i = 0; i < n; i++) {
            memo[i][i][1] = 0;
        }

        return calculate(stones, 0, n - 1, 1, K);
    }

    private int calculate(int[] stones, int i, int j, int piles, int K) {
        if ((j - i + 1 - piles) % (K - 1) != 0) {
            return Integer.MAX_VALUE;
        }
        if (memo[i][j][piles] != null) {
            return memo[i][j][piles];
        }
        int cost = Integer.MAX_VALUE;
        if (piles == 1) {
            int prev = calculate(stones, i, j, K, K);
            if (prev != Integer.MAX_VALUE) {
                cost = prev + preSum[j + 1] - preSum[i];
            }
        } else {
            for (int mid = i; mid < j; mid++) {
                int left = calculate(stones, i, mid, 1, K);
                if (left >= cost) continue;
                int right = calculate(stones, mid + 1, j, piles - 1, K);
                if (right >= cost) continue;
                cost = Math.min(cost, left + right);
            }
        }
        memo[i][j][piles] = cost;
        return cost;
    }

X.
https://leetcode.com/problems/minimum-cost-to-merge-stones/discuss/247686/Java-Solution-with-DP-Interval-6-ms

public int mergeStones(int[] stones, int K) {
 int n = stones.length;
 if (n % (K - 1) != 1 && K != 2) return -1;
 int[][] dp = new int[n][n];  // definition : dp[i][j] = min cost to merge [i, j]
 int[] prefixSum = new int[n + 1];
 for (int i = 1; i < n + 1; i++) { // sum[i, j] = prefixSum[j + 1] - prefixSum[i];
  prefixSum[i] = prefixSum[i - 1] + stones[i - 1];
 }
 for (int len = K; len <= n; len++) {
  for (int i = 0; i + len - 1 < n; i++) {
   int j = i + len - 1;
   dp[i][j] = Integer.MAX_VALUE;
   int s = len % (K - 1) == 1 || K == 2 ? len - (K - 1) : len; // base case
   for (int k = i + 1; k <= j; k++) {
    if ((k - i - 1) / (K - 1) + (j - k) / (K - 1) == (s - 1) / (K - 1)) { // check module
     int curCost = 0;
     if (i <= k - 1) curCost += dp[i][k-1];
     if (k <= j) curCost += dp[k][j];
     dp[i][j] = Math.min(dp[i][j], curCost);
    }
   }
   if (len % (K - 1) == 1 || K == 2) dp[i][j] += prefixSum[j + 1] - prefixSum[i];
  }
 }
 return dp[0][n - 1];
}

https://leetcode.com/problems/minimum-cost-to-merge-stones/discuss/247657/JAVA-Bottom-Up-DP-9ms

dp[i][j][k] represent the minimum cost when merge stones from i to j into k piles.
dp[i][j][k] = Math.min(dp[i][j][k], dp[i][t][k - 1] + dp[t + 1][j][1]) for t in range [i, j)
After each step, dp[i][j][1] = dp[i][j][K] + sum(i, j)
At last, we need to return dp[1][len][1], that is merge stones from first to last into 1 piles.
Similar problem include 312. Burst Balloons.

    public int mergeStones(int[] stones, int K) {
        int len = stones.length;
        if ((len - 1) % (K - 1) != 0) {
            return -1;
        }
        
        int i, j, k, l, t;
        
        int[] prefixSum = new int[len + 1];
        for (i = 1; i <= len; i++) {
            prefixSum[i] = prefixSum[i - 1] + stones[i - 1];
        }
        
        int max = 99999999;
        int[][][] dp = new int[len + 1][len + 1][K + 1];
        for (i = 1; i <= len; i++) {
            for (j = 1; j <= len; j++) {
                for (k = 1; k <= K; k++) {
                    dp[i][j][k] = max;
                }
            }
        }
        
        for (i = 1; i <= len; i++) {
            dp[i][i][1] = 0;
        }

        for (l = 2; l <= len; l++) {
            for (i = 1; i <= len - l + 1; i++) {
                j = i + l - 1;
                for (k = 2; k <= K; k++) {
                    for (t = i; t < j; t++) {
                        dp[i][j][k] = Math.min(dp[i][j][k], dp[i][t][k - 1] + dp[t + 1][j][1]);
                    }
                }

                dp[i][j][1] = dp[i][j][K] + prefixSum[j] - prefixSum[i - 1];   
            }
        }

        return dp[1][len][1];
    }

X.
https://leetcode.com/problems/minimum-cost-to-merge-stones/discuss/247567/JavaC%2B%2BPython-DP

we can simplify the third parameter m in DP.

stones[i] ~ stones[j] will merge as much as possible.

Finally (j - i) % (K - 1) + 1 piles will be left.

It's less than K piles and no more merger happens.

dp[i][j] means the minimum cost needed to merge stones[i] ~ stones[j].

Complexity
Time O(N^3/K) Space O(N^2)
It can be improved, but I think it's fine now.

Q: Why mid jump at step K - 1
A: We can merge K piles into one pile,
we can't merge K + 1 piles into one pile.
We can merge K + K - 1 piles into on pile,
We can merge K + (K - 1) * steps piles into one pile.

    public int mergeStones(int[] stones, int K) {
        int n = stones.length;
        if ((n - 1) % (K - 1) > 0) return -1;

        int[] prefix = new int[n+1];
        for (int i = 0; i <  n; i++)
            prefix[i + 1] = prefix[i] + stones[i];

        int[][] dp = new int[n][n];
        for (int m = K; m <= n; ++m)
            for (int i = 0; i + m <= n; ++i) {
                int j = i + m - 1;
                dp[i][j] = Integer.MAX_VALUE;
                for (int mid = i; mid < j; mid += K - 1)
                    dp[i][j] = Math.min(dp[i][j], dp[i][mid] + dp[mid + 1][j]);
                if ((j - i) % (K - 1) == 0)
                    dp[i][j] += prefix[j + 1] - prefix[i];
            }
        return dp[0][n - 1];

dp[l][i] := min cost to merge [i, i + l) into as less piles as possible. Number of merges will be (l-1) / (K – 1) and
Transition: dp[l][i] = min(dp[m][i] + dp[l – m][i + m]) for 1 <= m < l
if ((l – 1) % (K – 1) == 0) [i, i + l) can be merged into 1 pile, dp[l][i] += sum(A[i:i+l])

Time complexity: O(n^3 / k)
Space complexity: O(n^2)

  int mergeStones(vector<int>& stones, int K) {

    const int n = stones.size();

    if ((n - 1) % (K - 1)) return -1;

    vector<int> sums(n + 1);

    for (int i = 0; i < stones.size(); ++i) 

      sums[i + 1] = sums[i] + stones[i];

    const int kInf = 1e9;

    // dp[i][j] := min cost to merge subarray A[i] ~ A[j] into (j-i)%(K-1) + 1 piles

    vector<vector<int>> dp(n, vector<int>(n, kInf));

    for (int i = 0; i < n; ++i) dp[i][i] = 0;

    for (int l = 2; l <= n; ++l) // subproblem length 

      for (int i = 0; i <= n - l; ++i) { // start        

        int j = i + l - 1;

        for (int m = i; m < j ; m += K - 1) // split point

            dp[i][j] = min(dp[i][j], dp[i][m] + dp[m + 1][j]);

        // If the current length can be merged into 1 pile

        // The cost is independent of the merge orders.

        if ((l - 1) % (K - 1) == 0)

          dp[i][j] += sums[j + 1] - sums[i];

}

    return dp[0][n - 1];

}

X. https://leetcode.com/problems/minimum-cost-to-merge-stones/discuss/247657/JAVA-Bottom-Up-%2B-Top-Down-DP-With-Explaination

Let's first think this problem in a simple way, what if we can only merge 2 adjacent piles into one pile?

For given example [3,2,4,1], we will normally think this as a greedy problem, we always merge two relatively small piles.
[[3, 2], 4, 1] -> [5, [4, 1]] -> [5, 5] -> [10](cost: 20).

While one counterexample is [6,4,4,6],
if we merge greedily, [6, [4, 4], 6] -> [[6, 8], 6] -> [14, 6] -> [20] (cost: 42),
while the optimal way is [[6, 4], 4, 6] -> [10, [4, 6]] -> [10, 10] -> [20] (cost:40).

What if we think this problem reversely, which two piles should we merge at the last step?

We don't know which two piles to merge for now, but we can know the cost of that step, which is the sum of that two piles.
[3 | 2, 4, 1]
3 + 7 = 10
[3 , 2 | 4, 1]
5 + 5 = 10
[3 , 2, 4 | 1]
9 + 1 = 10
No matter how to split the two piles, the sum is always the sum of the two piles.

Now the only thing that matters is how to get the minimum cost to split to two piles.
So we need to know the minimum cost of merging left part to 1 pile, and minimum cost of merging right part to 1 pile, this is a typical sub problem.

State: Minimum cost merging piles from i to j to 1 pile.

Function: dp[i][j] = min(sum[i][j] + dp[i][k] + dp[k + 1][j]) (i <= k < j)

Init: dp[i][i] = 0 (Already a pile)

Answer: dp[1][len] (len is the stones number)

public int mergeStonesTwo(int[] stones) {
    if (stones == null || stones.length == 0) {
        return 0;
    }
    int len = stones.length;
    int max = Integer.MAX_VALUE;
    int[][] dp = new int[len + 1][len + 1];
    int[] prefixSum = new int[len + 1];
    int i, j, k, l;
    for (i = 1; i <= len; i++) {
        prefixSum[i] = prefixSum[i - 1] + stones[i - 1];
    }
    
    for (i = 1; i <= len; i++) {
        dp[i][i] = 0;
    }
    
    for (l = 2; l <= len; l++) {
        for (i = 1; i <= len - l + 1; i++) {
            j = i + l - 1;
            dp[i][j] = max;
            int sum = prefixSum[j] - prefixSum[i - 1];
            for (k = i; k < j; k++) {
                dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k + 1][j] + sum);
            }
        }
    }
    
    return dp[1][len];
}

Time Complexity: O(n ^ 3) (n is the number of stone)

During interview, this might be our first question, the follow-up may ask us what if we can merge x consecutive piles? Just like original problem.
Now our sub problem becomes: we need to know the minimum cost of merging left part to x - 1 piles and right part to 1 pile.
Our state has one more information to know, how many piles. So we add the field to our dp array.

State: Minimum cost merging piles from i to j to k pile.

Function:
dp[i][j][1] = dp[i][j][K] + sum[i][j] (dp[i][j][K] != max)
dp[i][j][k] = min(dp[i][t][k - 1] + dp[t + 1][j][1]) (t ∈ [i, j) && dp[i][t][k - 1] != max && dp[t+1][j][1] != max && k ∈ [2, K])

Init: dp[i][i][1] = 0 (Already a pile) others = max

Answer: dp[1][len][1] (len is the stones number)

Time Complexity: O(n^3 * K) (n is the number of stone)

Similar problem include 312. Burst Balloons. They are all dynamic programming problem related to interval.

The max value is somewhat confusing here, so I update the version using Integer.MAX_VALUE. The idea of MAX is to mark the invalid state. If we don't check, the res may be negative, cause Integer.MAX_VALUE + 1 = Integer.MIN_VALUE.

// bottom-up
    public int mergeStones(int[] stones, int K) {
        int len = stones.length;
        if ((len - 1) % (K - 1) != 0) {
            return -1;
        }
        
        int i, j, k, l, t;
        
        int[] prefixSum = new int[len + 1];
        for (i = 1; i <= len; i++) {
            prefixSum[i] = prefixSum[i - 1] + stones[i - 1];
        }
        
        int max = Integer.MAX_VALUE;
        int[][][] dp = new int[len + 1][len + 1][K + 1];
        for (i = 1; i <= len; i++) {
            for (j = 1; j <= len; j++) {
                for (k = 1; k <= K; k++) {
                    dp[i][j][k] = max;
                }
            }
        }
        
        for (i = 1; i <= len; i++) {
            dp[i][i][1] = 0;
        }

        for (l = 2; l <= len; l++) {
            for (i = 1; i <= len - l + 1; i++) {
                j = i + l - 1;
                for (k = 2; k <= K; k++) {
                    for (t = i; t < j; t++) {
                        if (dp[i][t][k - 1] == max || dp[t + 1][j][1] == max) {
                            continue;
                        }
                        dp[i][j][k] = Math.min(dp[i][j][k], dp[i][t][k - 1] + dp[t + 1][j][1]);
                    }
                }
                if (dp[i][j][K] == max) {
                    continue;
                }
                dp[i][j][1] = dp[i][j][K] + prefixSum[j] - prefixSum[i - 1];   
            }
        }

        return dp[1][len][1];
    }

// Top-down
    int[][][] dp;
    int max = Integer.MAX_VALUE;
    int K;
    
    public int mergeStones(int[] stones, int K) {
        this.K = K;
        int len = stones.length;
        if ((len - 1) % (K - 1) != 0) {
            return -1;
        }
        dp = new int[len + 1][len + 1][K + 1];
        int[] prefixSum = new int[len + 1];
        
        int i;
        for (i = 1; i <= len; i++) {
            prefixSum[i] = prefixSum[i - 1] + stones[i - 1];
        }
        
        getResult(prefixSum, 1, len, 1);
        return dp[1][len][1];
    }
    
    private int getResult(int[] prefixSum, int left, int right, int piles) {
        if (dp[left][right][piles] != 0) {
            return dp[left][right][piles];
        }
        int res = max;
        int t;
        if (left == right) {
            res = (piles == 1) ? 0 : max;
        }
        else {
            if (piles == 1) {
                int mergeK = getResult(prefixSum, left, right, K);
                if (mergeK != max) {
                    res = mergeK + prefixSum[right] - prefixSum[left - 1]; 
                }
            }
            else {
                for (t = left; t < right; t++) {
                    int l = getResult(prefixSum, left, t, piles - 1);
                    int r = getResult(prefixSum, t + 1, right, 1);
                    if (l != max && r != max) {
                        res = Math.min(res, l + r);
                    }
                }
            }
        }
        dp[left][right][piles] = res;
        return res;
    }

X. https://www.jiuzhang.com/solution/segment-stones-merge/

dp(i, j, k)代表合并[i, j]区间为k堆所需要最小代价
sum(i, j)代表sum(weight[i...j])
dp(i, j, k) = min(dp(i, t, k-1) + dp(t+1, j, 1))
dp(i, j, 1) = min(dp(i, j, t) + sum(i, j))

    public int getMinimumCost(int n, int left, int right, int[] weight) {
        // Write your code here
        int [] pre = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            pre[i] = pre[i - 1] + weight[i - 1];
        }
        int[][][]dp = new int[205][205][205];
        int INF = 1000000000;
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= n; j++) {
                for(int k = 1; k <= n; k++) {
                    dp[i][j][k] = INF;
                }
            }
        }
        for (int i = 1; i <= n; i++) {
            dp[i][i][1] = 0;
        }
        for (int len = 1; len <= n; len++) {
            for (int i = 1; i + len - 1 <= n; i++) {
                int j = i + len - 1;
                for (int k = 2; k <= len; k++) {
                    for (int t = i; t + 1 <= j; t++) {
                        dp[i][j][k] = Math.min(dp[i][j][k], dp[i][t][k - 1] + dp[t + 1][j][1]);
                    }
                }
                for (int k = left; k <= right; k++) {
                    dp[i][j][1] = Math.min(dp[i][j][1], dp[i][j][k] + pre[j] - pre[i - 1]);   
                }
            }
        }
        if (dp[1][n][1] >= INF) {
            return 0;
        }
        return dp[1][n][1];
    }
}
1

LeetCode 1000 - Minimum Cost to Merge Stones

Labels

Popular Posts