LeetCode 834 - Sum of Distances in Tree

https://leetcode.com/problems/sum-of-distances-in-tree/

An undirected, connected tree with N nodes labelled 0...N-1 and N-1 edges are given.

The ith edge connects nodes edges[i][0] and edges[i][1] together.

Return a list ans, where ans[i] is the sum of the distances between node i and all other nodes.

Example 1:

Input: N = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
Output: [8,12,6,10,10,10]
Explanation: 
Here is a diagram of the given tree:
  0
 / \
1   2
   /|\
  3 4 5
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.  Hence, answer[0] = 8, and so on.

Note: 1 <= N <= 10000

http://www.programmersought.com/article/1793330558/

What if given a tree, with a certain root 0?
In O(N) we can find sum of distances in tree from root and all other nodes.
Now for all N nodes?
Of course, we can do it N times and solve it in O(N^2).
C++ and Java may get accepted luckly, but it’s not what we want.

When we move our root from one node to its connected node, one part of nodes get closer, one the other part get further.
If we know exactly hom many nodes in both parts, we can solve this problem.

With one single traversal in tree, we should get enough information for it and don’t need to do it again and again.

Explanation:
0. Let’s solve it with node 0 as root.

Initial an array of hashset tree, tree[i] contains all connected nodes to i.
Initial an array count, count[i] counts all nodes in the subtree i.
Initial an array of res, res[i] counts sum of distance in subtree i.

Post order dfs traversal, update count and res:
count[root] = sum(count[i]) + 1
res[root] = sum(res[i]) + sum(count[i])

Pre order dfs traversal, update res:
When we move our root from parent to its child i, count[i] points get 1 closer to root, n - count[i] nodes get 1 futhur to root.
res[i] = res[root] - count[i] + N - count[i]

return res, done.

https://www.acwing.com/solution/LeetCode/content/619/
这里需要两次 DFS。假设 0 号结点为根结点，将整棵树变为有根树。
第一次 DFS 求出每个点子树的大小（包含自身），以及该结点到子树所有结点的距离之和。
第二次 DFS 需要累计每个结点从父亲获得的其他结点的距离之和。
具体地，第一次 DFS 时，假设当前结点是 xx，某个儿子是 yy，则num[x]=num[x]+num[y]num[x]=num[x]+num[y]，ans[x]=ans[x]+num[y]ans[x]=ans[x]+num[y]，最后 num[x]++num[x]++。
第二次 DFS 时，仍然假设当前结点为 xx，某个儿子是 yy，并且假设 ans[x]ans[x] 就是其他所有结点到当前结点的距离之和，接下来更新 ans[y]ans[y]。更新之前 ans[y]ans[y] 是 yy 及其子结点到达它的距离之和，需要补全经过 xx 到 yy 的结点：ans[y]=ans[y]+(ans[x]−(ans[y]+num[y])+(N−num[y]))ans[y]=ans[y]+(ans[x]−(ans[y]+num[y])+(N−num[y]))，即用 ans[x]ans[x] 除去经过 yy 到达 xx 的结点，然后将剩余的结点整体向 yy 移动一步，移动所带来的代价就是剩余的结点数 N−num[y]N−num[y]，就像第一次 DFS 更新时，每次所有儿子结点向当前结点移动一步所带来的更新就是儿子结点的个数。

https://chenboxie.wordpress.com/2018/06/02/leetcode-834-sum-of-distances-in-tree/

首先想到的用brute force去解这道题:
对于每个节点，我们用BFS就可以求出每个level的点到该节点的距离，边遍历边求和。但是我们要对每个节点都要做一次BFS，时间复杂度为O(n*n)

仔细分析，其实有非常多的重复计算，那么去重就是这道题的分析关键。
那么重复到底在哪里？拿题目中给出的例子来说：
在计算其他节点到N0(node0, 节点0)的距离和的时候：(第一次遍历)
distance(1,2) -> 0 = 1，distance(3,4,5) -> 0 = 2，假设3往下还有(6,7)两个节点，distance(6,7) -> 0 = 3

接下来我们计算其他节点到N2的距离和的时候：(第二次遍历)
distance(3,4,5) -> 2 = 1, distance(6,7) -> 2 = 2
可以看到，在第一次遍历，已经计算，并且知道N2下面有3个点(3,4,5),和两个二重degree(6,7), 第二次遍历，竟然又一次计算N2下面有多少个点，每个点到它的距离是多少，这就是重复的地方。

那么如何去重？这部分是最难想的
在第二次遍历的时候，可以发现，所有N2已经N2往下的节点都靠近了，而除此之外的节点都远离了，所以只要知道N2和N2往下的节点总共有多少个，并且存下来count(2), count(2)个数的节点，距离都要减1，n – count(2)个数的节点，距离都要增加1，最后可以得到公式：
res(2) = res(0) – count(2) + (n – count(2))

所以在第一次遍历的时候，要记录res(0), 和count(i), i from 0 to n – 1，通过这些信息，在第二次遍历的时候，通过刚才的公式，可以得到所有点的结果。

https://www.cnblogs.com/ZhaoxiCheung/p/LeetCode-SumofDistancesinTree.html
每个节点保存两个值，一个是其子树的节点个数（包括自身节点也要计数）nodesum[ ]，一个是其子树各点到它的距离 dp[ ]，那么我们假设根节点为 u ，其仅有一个儿子 v ， u 到 v 的距离为 1 ，而 v 有若干儿子节点，那么 dp[v] 表示 v 的子树各点到 v 的距离和，那么各个节点到达 u 的距离便可以这样计算： dp[u] = dp[v] + nodesum[ v ] *1; （式子的理解，v 的一个儿子节点为 f，那么 f 到达 u 的距离为  (sum[ f ->v] + sum [v- > u])*1 ，dp[v] 包含了 sum[f->v]*1，所以也就是式子的分配式推广到各个子节点计算出来的和）。我们已经知道了各个节点到达根节点的距离和，那么从根节点开始递推下来可以得到各个点的距离和。另开一个数组表示每个节点的到其他节点的距离和，那么对于根节点u来说， dissum[u] = dp[u]。以 u 的儿子 v 为例， v 的子节点到 v 不必经过 v->u 这条路径，因此 dissum[u] 多了 nodesum[v] * 1，但是对于不是 v 的子节点的节点，只到达了 u ，因此要到达 v 必须多走 u->v 这条路径，因此 dissum[u] 少了 ( N - nodesum[v] ) * 1) ,所以 dissum[v] = dissum[u] - nodesum[v] * 1 + (N - nodesum[v] ) * 1，按照这个方法递推下去就可以得到各个点的距离和。


https://leetcode.com/problems/sum-of-distances-in-tree/discuss/130583/C%2B%2BJavaPython-Pre-order-and-Post-order-DFS-O(N)

What if given a tree, with a certain root 0?
In O(N) we can find sum of distances in tree from root and all other nodes.
Now for all N nodes?
Of course, we can do it N times and solve it in O(N^2).
C++ and Java may get accepted luckly, but it's not what we want.

When we move our root from one node to its connected node, one part of nodes get closer, one the other part get further.
If we know exactly hom many nodes in both parts, we can solve this problem.

With one single traversal in tree, we should get enough information for it and don't need to do it again and again.

Explanation:
0. Let's solve it with node 0 as root.

1. Initial an array of hashset tree, tree[i] contains all connected nodes to i.
   Initial an array count, count[i] counts all nodes in the subtree i.
   Initial an array of res, res[i] counts sum of distance in subtree i.
2. Post order dfs traversal, update count and res:
   count[root] = sum(count[i]) + 1
res[root] = sum(res[i]) + sum(count[i])
3. Pre order dfs traversal, update res:
   When we move our root from parent to its child i, count[i] points get 1 closer to root, n - count[i] nodes get 1 futhur to root.
   res[i] = res[root] - count[i] + N - count[i]
4. return res, done.

    int[] res, count; ArrayList<HashSet<Integer>> tree; int n;
    public int[] sumOfDistancesInTree(int N, int[][] edges) {
        tree = new ArrayList<HashSet<Integer>>();
        res = new int[N];
        count = new int[N];
        n = N;
        for (int i = 0; i < N ; ++i ) tree.add(new HashSet<Integer>());
        for (int[] e : edges) {tree.get(e[0]).add(e[1]); tree.get(e[1]).add(e[0]);}
        dfs(0, new HashSet<Integer>());
        dfs2(0, new HashSet<Integer>());
        return res;
    }

    public void dfs(int root, HashSet<Integer> seen) {
        seen.add(root);
        for (int i : tree.get(root))
            if (!seen.contains(i)) {
                dfs(i, seen);
                count[root] += count[i];
                res[root] += res[i] + count[i];
            }
        count[root]++;
    }


    public void dfs2(int root, HashSet<Integer> seen) {
        seen.add(root);
        for (int i : tree.get(root))
            if (!seen.contains(i)) {
                res[i] = res[root] - count[i] + n - count[i];
                dfs2(i, seen);
            };
    }




https://leetcode.com/articles/sum-of-distances-in-tree/
Approach #1: Subtree Sum and Count [Accepted]

Let ans be the returned answer, so that in particular ans[x] be the answer for node x.

Naively, finding each ans[x] would take $O(N)$ time (where $N$ is the number of nodes in the graph), which is too slow. This is the motivation to find out how ans[x] and ans[y] are related, so that we cut down on repeated work.

Let's investigate the answers of neighboring nodes $x$ and $y$. In particular, say $xy$ is an edge of the graph, that if cut would form two trees $X$ (containing $x$) and $Y$ (containing $y$).

Then, as illustrated in the diagram, the answer for $x$ in the entire tree, is the answer of $x$ on $X$ "x@X", plus the answer of $y$ on $Y$ "y@Y", plus the number of nodes in $Y$ "#(Y)". The last part "#(Y)" is specifically because for any node z in Y, dist(x, z) = dist(y, z) + 1.

By similar reasoning, the answer for $y$ in the entire tree is ans[y] = x@X + y@Y + #(X). Hence, for neighboring nodes $x$ and $y$, ans[x] - ans[y] = #(Y) - #(X).

Algorithm

Root the tree. For each node, consider the subtree $S_{\text{node}}$ of that node plus all descendants. Let count[node] be the number of nodes in $S_{\text{node}}$, and stsum[node] ("subtree sum") be the sum of the distances from node to the nodes in $S_{\text{node}}$.

We can calculate count and stsum using a post-order traversal, where on exiting some node, the count and stsum of all descendants of this node is correct, and we now calculate count[node] += count[child] and stsum[node] += stsum[child] + count[child].

This will give us the right answer for the root: ans[root] = stsum[root].

Now, to use the insight explained previously: if we have a node parent and it's child child, then these are neighboring nodes, and so ans[child] = ans[parent] - count[child] + (N - count[child]). This is because there are count[child] nodes that are 1 easier to get to from child than parent, and N-count[child] nodes that are 1 harder to get to from child than parent.

Using a second, pre-order traversal, we can update our answer in linear time for all of our nodes.

  int[] ans, count;

  List<Set<Integer>> graph;

  int N;

  public int[] sumOfDistancesInTree(int N, int[][] edges) {

    this.N = N;

    graph = new ArrayList<Set<Integer>>();

    ans = new int[N];

    count = new int[N];

    Arrays.fill(count, 1);

    for (int i = 0; i < N; ++i)

      graph.add(new HashSet<Integer>());

    for (int[] edge : edges) {

      graph.get(edge[0]).add(edge[1]);

      graph.get(edge[1]).add(edge[0]);

    }

    dfs(0, -1);

    dfs2(0, -1);

    return ans;

  }

  public void dfs(int node, int parent) {

    for (int child : graph.get(node))

      if (child != parent) {

        dfs(child, node);

        count[node] += count[child];

        ans[node] += ans[child] + count[child];

      }

  }

  public void dfs2(int node, int parent) {

    for (int child : graph.get(node))

      if (child != parent) {

        ans[child] = ans[node] - count[child] + N - count[child];

        dfs2(child, node);

      }

  }

https://techblog32895888.wordpress.com/2018/05/14/lc834-sum-distance-in-tree/

The following dfs algorithm is O(N^2) and gets TLE.

    vector<int> sumOfDistancesInTree(int N, vector<vector<int>>& edges) {
        vector<vector<int>> adj(N);
        for(int i=0;i<edges.size();i++)
        {
            adj[edges[i][0]].push_back(edges[i][1]);
            adj[edges[i][1]].push_back(edges[i][0]);
        }
        vector<int> distsum(N);
        vector<vector<int>> dist(N,vector<int>(N,-1));
        for(int i=0;i<N;i++) dist[i][i]=0;
        int len=0;
        for(int i=0;i<N;i++)
        {
            dfs(i,adj,-1,distsum[i],len);
        }
        return distsum;
    }
    int dfs(int root,vector<vector<int>>& adj,int parent,int& res,int& len)
    {
        //int len=0;
        for(int i=0;i<adj[root].size();i++)
        {
            int nd=adj[root][i];
            if(nd==parent) continue;
            len++;
            dfs(nd,adj,root,res,len);//
            res+=len;
            len--;
        }
        //cout<<root<<": "<<len<<endl;
        return len;
    }

There are many recalculations in above algorithm. For example, when we have 1 as the root, 0 becomes its child and 0’s child is already calculated. And the relation is easy to see: all 0’s children are now 1 farther and all 1’s previous children are 1 node nearer:

res[1]=res[0]-cnt[1]+(n-cnt[1])

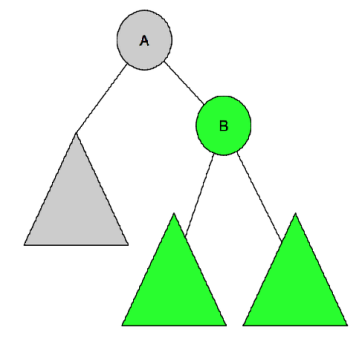
In the following graph, when we choose A’s child B as the new root, All nodes for the B subtree will subtract one (the green one), all the remaining nodes will add one (N-green)

One post-order traversal (first child and then parent node) will be able to get the cnt array and the distsum. cnt[i] is the number of node for the subtree i, and distsum[i] is the distance sum for subtree i.

cnt[i]=sum(cnt[child])+1
distsum[i]=sum(distsum[child])+sum(cnt[i])

The 1st equation: add all children plus one root node

The 2nd equation is not that clear: if we want to get distsum[i] we first get the sum of all its children, but the root needs go to every its child/grand child nodes, which is the distsum requires) and that one is missing, and that item is the node number under it, which is cnt[root]-1.

After this step, we need change the root. Its child can be easily calculated using its parent. Recursively we first parent, then child, this can be done by pre-order traversal.

So the idea is now more clear:

we first build the cnt and distsum array for each node assuming the node 0 is root! (Note the distsum other than node 0 is ONLY the subtree) using post-order traversal.

After that, we need choose 0’s children as the root, and calculate the distsum using above equation using pre-order traversal. (as we can see, in this step BFS can also do this, but dfs is more concise and concept clear).

This problem is hard if you are not familiar with the dfs recursive approach.

As in the straightforward approach, we always need to avoid cyclic calculation which leads to infinite loops, we can use visited array or hashset to achieve this.

The following code is from the LC community most voted one:

    vector<int> sumOfDistancesInTree(int N, vector<vector<int>>& edges) 
    {
        vector<unordered_set<int>> tree(N);//adjacent matrix
        vector<int> res(N, 0);
        vector<int> count(N, 0);
        if (N == 1) return res;
        for (auto e : edges) 
        {
            tree[e[0]].insert(e[1]);
            tree[e[1]].insert(e[0]);
        }
        unordered_set<int> seen1, seen2;
        dfs(0, seen1, tree, res, count);
        dfs2(0, seen2, tree, res, count, N);
        return res;
    }

    void dfs(int root, unordered_set<int>& seen, vector<unordered_set<int>>& tree, vector<int>& res, vector<int>& count) 
    {
        seen.insert(root);
        for (auto i : tree[root])//root as a root tree
        {
            if (!seen.count(i)) //not visited
            {
                dfs(i, seen, tree, res, count); //child first
                count[root] += count[i];
                res[root] += res[i] + count[i]; //later the root
            }
        }
        count[root]++;
    }

    void dfs2(int root, unordered_set<int>& seen, vector<unordered_set<int>>& tree, vector<int>& res, vector<int>& count, int N) 
    {
        seen.insert(root);
        for (auto i : tree[root])
        {
            if (!seen.count(i)) 
            {
                res[i] = res[root] - count[i] + N - count[i];
                dfs2(i, seen, tree, res, count, N);
            }
        }
    }

https://leetcode.com/problems/sum-of-distances-in-tree/discuss/142858/Java-Accepted-concise-solution-with-DFS-and-built-into-graph-memoization

    public int[] sumOfDistancesInTree(int N, int[][] edges) {
        if (N == 1) {
            return new int[N];
        }
        if (N == 2) {
            return new int[]{1, 1};
        }
        
        List<int[]>[] graph = new ArrayList[N];
        for (int i = 0; i < N; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int i = 0; i < edges.length; i++) {
            // [0] = to  [1] = sum  [2] = num
            graph[edges[i][0]].add(new int[]{edges[i][1], 0, 0}); 
            graph[edges[i][1]].add(new int[]{edges[i][0], 0, 0});
        }
        
        int[] result = new int[N];
        boolean[] seen = new boolean[N];
        for (int i = 0; i < N; i++) {
            result[i] = dfs(graph, i, seen)[0];
        }
        return result;
    }

    private int[] dfs(List<int[]>[] graph, int i, boolean[] seen) {
        seen[i] = true;
        int sum = 0;
        int num = 1;
        for (int[] adj : graph[i]) {
            if (!seen[adj[0]]) {
                if (adj[1] == 0 && adj[2] == 0) {
                    int[] res = dfs(graph, adj[0], seen);
                    adj[1] = res[0];
                    adj[2] = res[1];
                }
                sum += (adj[1] + adj[2]);
                num += adj[2];
            }
        }
        seen[i] = false;
        return new int[]{sum, num};
    }

https://code.dennyzhang.com/sum-of-distances-in-tree
- better method names: dfsCnt, dfsDistance

// Basic Ideas: dfs, hashmap
// Complexity: Time O(n) Space O(n)
var m_edges map[int][]int

// No need to use hashmap here
var m_childcnt []int
var m_distances []int

func dfsCnt(node int, parent int, distance int) int {
    m_distances[0] += distance
    res := 1
    for _, child := range m_edges[node] {
        if child != parent {
            res += dfsCnt(child, node, distance+1)
        }
    }
    m_childcnt[node] = res
    return res
}

func dfsDistance(node int, parent int, N int) {
    if parent != -1 {
        m_distances[node] = m_distances[parent] + N - 2*m_childcnt[node]
    }
    for _, child := range m_edges[node] {
        if parent != child { dfsDistance(child, node, N) }
    }
}

func sumOfDistancesInTree(N int, edges [][]int) []int {
    m_edges = map[int][]int{}
    for i, _ := range edges {
        edge := edges[i]
        m_edges[edge[0]] = append(m_edges[edge[0]], edge[1])
        m_edges[edge[1]] = append(m_edges[edge[1]], edge[0])
    }
    m_childcnt = make([]int, N)
    m_distances = make([]int, N)
    m_distances[0] = 0
    dfsCnt(0, 0, 0)
    dfsDistance(0, -1, N)
    return m_distances
}

X. Different
http://www.programmersought.com/article/4207240893/