Merging with smaller auxiliary array

https://www.cnblogs.com/evasean/p/7220112.html

Suppose that the subarray a[0] to a[n-1] is sorted and the subarray a[n] to a[2*n-1] is sorted. How can you merge the two subarrays so that a[0] to a[2*n-1] is sorted using an auxiliary array of length n (instead of 2n)

分析：

对两个大小分别为n的有序子数组进行归并，要求空间复杂度为n，正常情况下归并排序在此处的空间复杂度为2n，但是由于两个子数组分别是有序的，故用大小为n的额外子空间辅助归并是个很合理的要求

 5     private static boolean less(Comparable v, Comparable w) {
 6         return v.compareTo(w) < 0;
 7     }
 8     public static void merge(Comparable[] array){
 9         int n = array.length/2;
10         Comparable[] aux = new Comparable[n];
11         for(int i=0;i<n;i++){ //取左半边sorted的元素至辅助数组，因为未来归并左侧位置可能会被右侧元素占据
12             aux[i] = array[i];
13         }
14         System.out.println(Arrays.toString(aux));
15         int l = 0;
16         int r = n;
17         for(int k = 0; k<2*n;k++){
18             if(l >= n) break;//辅助元素数组全部用完，array右侧不需要挪动位置了
19             else if(r>=2*n) array[k]=aux[l++];//array原右侧元素全部放置合适位置，后面只需把辅助数组的元素挪到array右侧
20             else if(less(array[r],aux[l])) array[k] = array[r++];
21             else array[k] = aux[l++];
22         }
23     }

http://seanzhou1023.blogspot.com/2017/04/quiz-5-princeton-algorithm.html
1. merge smallest n items into auxiliary array
2. compact the left items to a[n] - a[2*n-1]
3. copy back from auxiliary array to a[0]-a[n]
4. merge the left n items into auxiliary array

5. copy back from auxiliary arrary to a[n] - a[2*n-1]
https://www.peierlong.com/2017/12/18/Merging%20with%20smaller%20auxiliary%20array/#Java%E5%AE%9E%E7%8E%B0

https://www.geeksforgeeks.org/merge-two-sorted-arrays-o1-extra-space/

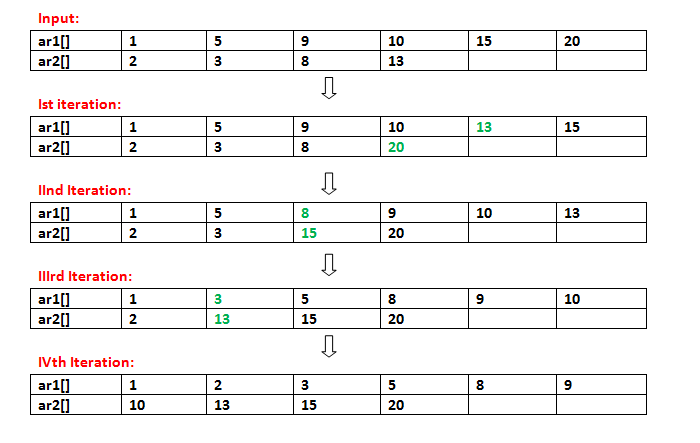
We are given two sorted array. We need to merge these two arrays such that the initial numbers (after complete sorting) are in the first array and the remaining numbers are in the second array. Extra space allowed in O(1).

Example:

Input: ar1[] = {10};
       ar2[] = {2, 3};
Output: ar1[] = {2}
        ar2[] = {3, 10}  

This task is simple and O(m+n) if we are allowed to use extra space. But it becomes really complicated when extra space is not allowed and doesn’t look possible in less than O(m*n) worst case time.

The idea is to begin from last element of ar2[] and search it in ar1[]. If there is a greater element in ar1[], then we move last element of ar1[] to ar2[]. To keep ar1[] and ar2[] sorted, we need to place last element of ar2[] at correct place in ar1[]. We can use Insertion Sort type of insertion for this. Below is algorithm:

1) Iterate through every element of ar2[] starting from last 
   element. Do following for every element ar2[i]
    a) Store last element of ar1[i]: last = ar1[i]
    b) Loop from last element of ar1[] while element ar1[j] is 
       smaller than ar2[i].
          ar1[j+1] = ar1[j] // Move element one position ahead
          j--
    c) If any element of ar1[] was moved or (j != m-1)
          ar1[j+1] = ar2[i] 
          ar2[i] = last  

In above loop, elements in ar1[] and ar2[] are always kept sorted.

    static int arr1[] = new int[]{1, 5, 9, 10, 15, 20};

    static int arr2[] = new int[]{2, 3, 8, 13};

      

    static void merge(int m, int n)

    {

        // Iterate through all elements of ar2[] starting from

        // the last element

        for (int i=n-1; i>=0; i--)

        {

            /* Find the smallest element greater than ar2[i]. Move all

               elements one position ahead till the smallest greater

               element is not found */

            int j, last = arr1[m-1];

            for (j=m-2; j >= 0 && arr1[j] > arr2[i]; j--)

                arr1[j+1] = arr1[j];

       

            // If there was a greater element

            if (j != m-2 || last > arr2[i])

            {

                arr1[j+1] = arr2[i];

                arr2[i] = last;

            }

        }

    }