Codility - Lesson 4: Number of Disc Intersections

Codility and other programming lessons: Lesson 4: NumberOfDiscIntersections (Number of DiscIntersections)
https://codility.com/programmers/lessons/4

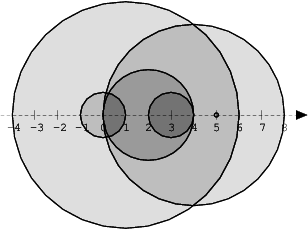
We draw N discs on a plane. The discs are numbered from 0 to N − 1. A zero-indexed array A of N non-negative integers, specifying the radiuses of the discs, is given. The J-th disc is drawn with its center at (J, 0) and radius A[J].

We say that the J-th disc and K-th disc intersect if J ≠ K and the J-th and K-th discs have at least one common point (assuming that the discs contain their borders).

The figure below shows discs drawn for N = 6 and A as follows:

  A[0] = 1
  A[1] = 5
  A[2] = 2
  A[3] = 1
  A[4] = 4
  A[5] = 0

There are eleven (unordered) pairs of discs that intersect, namely:

• discs 1 and 4 intersect, and both intersect with all the other discs;
• disc 2 also intersects with discs 0 and 3.

http://codility-lessons.blogspot.com/2015/02/lesson-4-numberofdiscintersections.html
1. a very simple solution
One of the easiest solutions would be to check each disc one-by-one, seeing how many other discs have intersection.
int solution(int A[], int N) 
{   
    int cnt = 0;     int i, j;     
    for (i = 0; i < N - 1; i++){         long long curl = (long long)i - A[i];         long long curr = (long long)i + A[i];         for (j = i + 1; j < N; j++){             long long posl = (long long)j - A[j];              long long posr = (long long)j + A[j];              
            if (posl <= curr && curl <= posr){                  cnt++;                  if (cnt > 10000000){                      return -1;                  }              }           }     }   return cnt; }

http://gaohow.com/blog/article?id=8

If we change the geometry of disc to segments on x-axis, the result should be the same.

We can see, for a segment A (x, y), the number of intersections equals

number of segments occurred before y - number of complete segments before y - itself
=number of starting points before y - number of ending points  before y - 1

Because, if segment (w, z) is in (x, y), the section is counted when we we compute the segment (w, z).

public int solution(int[] a) { int MAX = 10000000; long[] starts = new long[a.length]; long[] endings = new long[a.length]; //as the radius is integer, the ending points may be greater than 2^31 - 1 for (int i = 0; i < a.length; i++) { starts[i] = i - (long)a[i]; endings[i] = i + (long)a[i]; } Arrays.sort(starts); Arrays.sort(endings); int num = 0; int startIndex = 0; for (int endingIndex = 0; endingIndex < endings.length - 1; endingIndex++) { while (startIndex < starts.length && starts[startIndex] <= endings[endingIndex]) { startIndex += 1; } num += startIndex - endingIndex - 1; if (num > MAX) { return -1; } } return num; }
we convert the 2D problem into 1D. Because all the circles’ center is on x-axis, we can flat them into a 1D segment as [center-radius, center+radius]. Then the number of (unordered) pairs of intersecting discs is the number of intersecting segments.
http://www.lucainvernizzi.net/blog/2014/11/21/codility-beta-challenge-number-of-disc-intersections/

def solution(A):
    events = []
    for i, a in enumerate(A):
        events += [(i-a, +1), (i+a, -1)]
    events.sort(key=lambda x: (x[0], -x[1]))
    intersections, active_circles = 0, 0
    for _, circle_count_delta in events:
        intersections += active_circles * (circle_count_delta > 0)
        active_circles += circle_count_delta
        if intersections > 10E6:
            return -1
    return intersections

https://github.com/frncsrss/interviews/blob/master/src/core/interviews/arrays/DiscIntersection.java
   * Time complexity:  O(nlogn)
   * Space complexity: O(n)
  public static int f2(int[] radius) {
    final int n = radius.length;

    // transform the array of n radius into an array of n intervals
    Interval[] intervals = new Interval[n];
    for(int i = 0; i < n; i++) {
      intervals[i] = new Interval(i - radius[i], i + radius[i]);
    }
    // sort the intervals in ascending lower bound then ascending upper bound
    Arrays.sort(intervals, new Comparator<Interval>() {  // O(nlogn)
      @Override
      public int compare(Interval i1, Interval i2) {
        if(i1.lo > i2.lo) {
          return 1;
        } else if(i1.lo < i2.lo) {
          return -1;
        }
        return new Integer(i1.hi).compareTo(i2.hi);
      }
    });

    int count = 0;
    for(int i = 0; i < n - 1; i++) {  // O(nlogn)
      // binary search of intervals[i].hi in intervals[i+1...n-1], O(logn)
      final int value = intervals[i].hi;
      int lo = i + 1;
      int hi = n - 1;
      while(lo <= hi) {
        int mid = lo + (hi - lo) / 2;
        if(intervals[mid].lo > value) {
          hi = mid - 1;
        } else {
          lo = mid + 1;
        }
      }

      count += hi - i;
    }
    return count;
  }

   * Time complexity:  O(nlogn)
   * Space complexity: O(n)
   */
  public static int f3(int[] radius) {
    final int n = radius.length;

    // transform the array of n radius into an array of 2n boundaries
    Endpoint[] boundaries = new Endpoint[2 * n];
    for(int i = 0; i < n; i++) {
      boundaries[i] = new Endpoint(Endpoint.Type.START, i - radius[i]);
      boundaries[i + n] = new Endpoint(Endpoint.Type.END, i + radius[i]);
    }
    // sort the boundaries
    Arrays.sort(boundaries);

    int count = 0;
    int start = 0;
    for(int i = 0; i < 2 * n; i++) {
      if(Endpoint.Type.START.equals(boundaries[i].type)) {
        start++;
      } else {
        start--;
        count += start;
      }
    }
    return count;
  }

  private static class Endpoint implements Comparable<Endpoint> {
    public static enum Type {START, END};

    private final Type type;  // start or end boundary
    private final int v;

    public Endpoint(Type type, int value) {
      this.type = type;
      this.v = value;
    }

    @Override
    public int compareTo(Endpoint that) {
      if(this.v < that.v) return -1;
      if(this.v > that.v) return +1;
      // switch sign if exclusive ending range endpoint
      if(Type.START.equals(this.type) && Type.END.equals(that.type)) return -1;
      if(Type.END.equals(this.type) && Type.START.equals(that.type)) return +1;
      return 0;
    }
  }

O(N)  https://zhengxucoding.wordpress.com/2015/04/11/codility-numberofdiscintersections/
https://stackoverflow.com/questions/4801242/algorithm-to-calculate-number-of-intersecting-discs/27549852

1:   public int solutionLinear(int[] a) {  
2:      long result = 0;  
3:      int[] dps = new int[a.length];  
4:      int[] dpe = new int[a.length];  
5:      for (int i = 0; i < a.length; i++) {  
6:        // stores the number of discs that starts at i-a[i]  
7:        dps[Math.max(0, i - a[i])]++;  
8:        if (i < a.length - a[i])  
9:          dpe[i + a[i]]++; // stores the number of discs that ends at i+a[i]  
10:      }  // dpe[Math.min(a.length - 1, i + a[i])]++; should use this
11:      long t = 0;// t is the number of discs that have started and have not ended yet  
12:      for (int i = 0; i < a.length; i++) {  
13:        if (dps[i] > 0) {// there are discs that start at this position  
14:          // discs that started before and the discs that started just now all intersect  
15:          result += t * dps[i];  
16:          // discs that started just now also intersect with each other  
17:          // the number of pairs is dps[i]!/(2! * dps[i]-2)!)  
18:          result += dps[i] * (dps[i] - 1) / 2;  
19:          if (result > 10000000) {  
20:            return -1;  
21:          }  
22:          // we add the new discs to the set of discs that have started, but not ended.  
23:          t += dps[i];  
24:        }  
25:        // At position i, there could be some discs that end,  
26:        // and thus, we must update t by removing the discs that have ended at i.  
27:        t -= dpe[i];  
28:      }  
29:      return (int) result;  
30:    }  

Attempt 1 - Brute Force
http://rafal.io/posts/codility-intersecting-discs.html
Let’s first try to come up with a brute force solution – this is always a good start.

Given array indices i,j (j>i), if the discs are located at (0,i) and (0,j) respectively, then the discs will intersect iff the following holds:

j−i≤A[i]+A[j]

Given this predicate, simply iterate over array A, and check for how many subsequent discs the above predicate holds. This gives us an O(n2) algorithm.

One of the easiest solutions would be to check each disc one-by-one, seeing how many other discs have intersection.

int solution(int A[], int N)
{  
    int cnt = 0;
    int i, j;
 
    for (i = 0; i < N - 1; i++){
        long long curl = (long long)i - A[i];
        long long curr = (long long)i + A[i];
     
        for (j = i + 1; j < N; j++){
            long long posl = (long long)j - A[j];
            long long posr = (long long)j + A[j];
                       
            if (posl <= curr && curl <= posr){
                cnt++;
                if (cnt > 10000000){
                    return -1;
                }
            }          
        }
    }
    return cnt;
}
Improving to O(NlogN)

We can rewrite the above predicate:

j−i≤A[i]+A[j]A[i]+i≥−(A[j]−j)

Now we are getting closer to a solution. We see that the solution is dependent on a ≥ predicate where each side is a linear transformation of the input array A. We can proceed as follows:

1. Produce two arrays containing A[i]+i and −(A[j]−j).
2. Sort them - O(Nlog(N))
3. Compute for how many pairs the above predicate holds.

To do the last step above, simply go through array with sorted values A[i]+i, and for each valuex, check how many values from the sorted array −(A[j]−j) are smaller than x. This can be done with binary search in O(log(N)).

Crucially, we must subtract what was counted twice and any degenerate solutions – these where the predicate j−i≤A[i]+A[j] holds true since j−i≤0. To do this, subtract N∗(N+1)2 from the total.

 public static int intersectingDiscs(int[] A){
    int l = A.length;

    long[] A1 = new long[l]; // upgrade to avoid overflow
    long[] A2 = new long[l];
    
    for(int i = 0; i < l; i++){
      A1[i] = (long)A[i] + i;
      A2[i] = -((long)A[i]-i);
    }
    
    Arrays.sort(A1);
    Arrays.sort(A2);
    
    long cnt = 0;
    
    for(int i = A.length - 1; i >= 0; i--){
      int pos = Arrays.binarySearch(A2, A1[i]);
      if(pos >= 0){ // we can use one binary search to get left most, one to get right most
        while(pos < A.length && A2[pos] == A1[i]){
          pos++;
        }
        cnt += pos;
      } else{ // element not there
        int insertionPoint = -(pos+1);
        cnt += insertionPoint;
      }
      
    }
    
    long sub = (long)l*((long)l+1)/2;
    cnt = cnt - sub;
              
    if(cnt > 1e7) return -1;
    
    return (int)cnt;
  }

X. https://codesolutiony.wordpress.com/2015/01/04/codility-4-1-number-of-disc-intersections/

    public int solution(int[] A) {

        // write your code in Java SE 8

        long[][] intervals = new long[A.length][2];

        for (int i = 0; i < A.length; i++) {

            intervals[i][0] = (long)i - A[i];

            intervals[i][1] = (long)i + A[i];

        }

        Arrays.sort(intervals, new Comparator<long[]>() {

            public int compare(long[] a, long[] b) {

                return Long.compare(a[0],b[0]);

            }

        });

        int result = 0;

        for (int i = 0; i < A.length; i++) {

            result += findSub(intervals, intervals[i][1], i+1);

            if (result > 10000000) {

                return -1;

            }

        }

        return result;

    }

    private int findSub(long[][] intervals, long time, int index) {

        int start = index;

        int end = intervals.length - 1;

        int result = 0;

        while (start <= end) {

            int mid = (start + end) / 2;

            if (intervals[mid][0] <= time) {

                result += mid - start + 1;

                start = mid + 1;

            } else {

                end = mid - 1;

            }

        }

        return result;

    }

http://codesays.com/2014/solution-to-beta2010-number-of-disc-intersections-by-codility/

def solution(A):

    discs_count = len(A)            # The total number of discs

    range_upper = [0]*discs_count   # The upper limit position of discs

    range_lower = [0]*discs_count   # The lower limit position of discs

    # Fill the limit_upper and limit_lower

    for index in xrange(0, discs_count):

        range_upper[index] = index + A[index]

        range_lower[index] = index - A[index]

    range_upper.sort()

    range_lower.sort()

    range_lower_index = 0

    intersect_count = 0

    for range_upper_index in xrange(0, discs_count):

        # Compute for each disc

        while range_lower_index < discs_count and \

            range_upper[range_upper_index] >= range_lower[range_lower_index]:

            # Find all the discs that:

            #    disc_center - disc_radius <= current_center + current_radius

            range_lower_index += 1

        # We must exclude some discs such that:

        #    disc_center - disc_radius <= current_center + current_radius

        #    AND

        #    disc_center + disc_radius <(=) current_center + current_radius

        # These discs are not intersected with current disc, and below the

        #    current one completely.

        # After removing, the left discs are intersected with current disc,

        #    and above the current one.

        # Attention: the current disc is intersecting itself in this result

        #    set. But it should not be. So we need to minus one to fix it.

        intersect_count += range_lower_index - range_upper_index -1

        if intersect_count > 10000000:

            return -1

    return intersect_count

http://blog.csdn.net/caopengcs/article/details/9327069
http://stackoverflow.com/questions/14042447/counting-disk-intersections-using-treeset
Read full article from Codility and other programming lessons: Lesson 4: NumberOfDiscIntersections (Number of DiscIntersections)