https://blog.codinghorror.com/the-danger-of-naivete/
http://eli.thegreenplace.net/2010/05/28/the-intuition-behind-fisher-yates-shuffling/
https://spin.atomicobject.com/2014/08/11/fisher-yates-shuffle-randomization-algorithm/
Fisher–Yates shuffle - Wikipedia, the free encyclopedia
The basic method given for generating a random permutation of the numbers 1 through N goes as follows:
http://adelzhang.blogspot.com/2012/09/knuth-shuffle.html
http://my.oschina.net/xlplbo/blog/312231
递归思想。我们有n张牌,不妨先假设有一个洗牌函数shuffle(....),能完美的洗出n-1张牌 。拿第n张牌来打乱前面n-1的洗牌顺序,从而得到n张牌的最终结果。
http://adelzhang.blogspot.com/2012/09/knuth-shuffle.html
How to choose randomly from a sequence of unknown length. The typical use is to choose a random line from a file.
The naive way to do it is to read the whole file, count the number of lines, choose a random number in that range, and that's your line. But that requires either holding the whole file in memory, or reading the file twice.
It turns out you don't need to know the length of the sequence in advance, you can choose as you go so that the end result is uniform. The cleverer way to do it is to choose a line with a decreasing probability as the sequence goes along, so that at any time, you have an element from the sequence with a uniform probability:
def random_element(seq):
"""Return an element chosen at random from `seq`."""
it = None
for n, elem in enumerate(seq):
if random.randint(0, n) == 0:
it = elem
return it
https://eyalsch.wordpress.com/2010/04/01/random-sample/
Sometimes our collection is not random access, so we have no choice but to traverse it completely in the worst case.
Random sample from a long linked list
Stream of items
http://eli.thegreenplace.net/2010/05/28/the-intuition-behind-fisher-yates-shuffling/
https://spin.atomicobject.com/2014/08/11/fisher-yates-shuffle-randomization-algorithm/
Fisher–Yates shuffle - Wikipedia, the free encyclopedia
The basic method given for generating a random permutation of the numbers 1 through N goes as follows:
- Write down the numbers from 1 through N.
- Pick a random number k between one and the number of unstruck numbers remaining (inclusive).
- Counting from the low end, strike out the kth number not yet struck out, and write it down elsewhere.
- Repeat from step 2 until all the numbers have been struck out.
- The sequence of numbers written down in step 3 is now a random permutation of the original numbers.
To shuffle an array a of n elements (indices 0..n-1):
for i from n − 1 downto 1 do
j ← random integer with 0 ≤ j ≤ i
exchange a[j] and a[i]
- Random random = new Random();
- for (int i = cards.size() - 1; i >= 0; i--) {
- int j = random.nextInt(i + 1);
- /* swap cards i,j */
- Card card = cards.get(i);
- cards.set(i, cards.get(j));
- cards.set(j, card);
- }
void ShuffleArray_Fisher_Yates(char* arr, int len){ int i = len, j; char temp; if ( i == 0 ) return; while ( --i ) { j = rand() % (i+1); temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; }}//To shuffle an array a of n elements (indices 0..n-1):for i from n − 1 downto 1 do j <- random integer with 0 ≤ j ≤ i exchange a[j] and a[i] |
这个算法就地洗牌,但它需要预先知道洗牌数组的长度。
http://my.oschina.net/xlplbo/blog/312231
递归思想。我们有n张牌,不妨先假设有一个洗牌函数shuffle(....),能完美的洗出n-1张牌 。拿第n张牌来打乱前面n-1的洗牌顺序,从而得到n张牌的最终结果。
//随机指定区域内的数int MyRand(int low, int high){ return low + rand() % (high - low + 1);}int* shuffle(int* cards, int n){ if (n <= 0) return cards; shuffle(cards, n - 1); int rand = MyRand(0, n); int temp = cards[rand]; cards[rand] = cards[n]; cards[n] = temp; return cards;}
Knuth-shuffle还有另一种实现:
1
2
3
4
5
6
7
| //To initialize an array a of n elements to a randomly shuffled copy of//source, both 0-based: a[0] <- source[0]for i from 1 to n − 1 do j <- random integer with 0 ≤ j ≤ i a[i] <- a[j] a[j] <- source[i] |
这个实现的正确性可以这么考虑:对于n-1次random调用生成的n!次随机序列,总会对应不 同的排列,所以n!次排列是均匀分布的。
这个实现有一个坏处,它需要额外的数组来存储生成的排列。但它也有一个大大的好处,它 可以不用预先知道数组的长度:
1
2
3
4
5
6
7
8
9
| //To initialize an empty array a to a randomly shuffled copy of source whose//length is not know:while source.moreDataAvailable j <- random integer with 0 ≤ j ≤ a.length if j = a.length a.append(source.next) else a.append(a[j]) a[j] <- source.next |
Knuth-Durstenfeld Shuffle 是一个in-place算法,原始数据被直接打乱,有些应用中可能需要保留原始数据,因此需要开辟一个新数组来存储打乱后的序列。Inside-Out Algorithm 算法的基本思想是设一游标i从前向后扫描原始数据的拷贝,在[0, i]之间随机一个下标j,然后用位置j的元素替换掉位置i的数字,再用原始数据位置i的元素替换掉拷贝数据位置j的元素。其作用相当于在拷贝数据中交换i与j位置处的值。伪代码如下:
def shuffle(lis): result = lis[:] for i in range(1, len(lis)): j = random.randrange(0, i) result[i] = result[j] result[j] = lis[i] return result
http://adelzhang.blogspot.com/2012/09/knuth-shuffle.html
//error!for(int i=0;i<cards.Length;i++){ int n = rand.Next(cards.Length); Swap(ref cards[i],ref cards[n]);}
Knuth-shuffle做些修改还可以有别的应用。比如下面这个问题:
- 如何从未知长度的序列中均匀地随机选择一个数?要求最多只遍历一遍。
- 如何从未知长度的序列中均匀地随机选择k个数?要求最多只遍历一遍。
How to choose randomly from a sequence of unknown length. The typical use is to choose a random line from a file.
The naive way to do it is to read the whole file, count the number of lines, choose a random number in that range, and that's your line. But that requires either holding the whole file in memory, or reading the file twice.
It turns out you don't need to know the length of the sequence in advance, you can choose as you go so that the end result is uniform. The cleverer way to do it is to choose a line with a decreasing probability as the sequence goes along, so that at any time, you have an element from the sequence with a uniform probability:
def random_element(seq):
"""Return an element chosen at random from `seq`."""
it = None
for n, elem in enumerate(seq):
if random.randint(0, n) == 0:
it = elem
return it
For the inductive case, imagine we've read N-1 elements already, and "it" is a random element chosen uniformly from those N-1 elements. The chance that the Nth element should be chosen instead is 1/N, because at this point, the chance that any particular line should be "it" is 1/N. So we choose a random number, and if it's the 1/N outcome, we take the Nth line as "it." In the case that we don't take the new line, which is (N-1)/N, the old line is kept. It was chosen randomly from the N-1 lines that preceded this one, so each line has a final chance of ((N-1)/N)/(N-1), or 1/N, or being chosen. Therefore the new line and each of the old lines is equally likely, so the distribution is uniform.
The original question had to do with picking 10 random lines, so how do we generalize to a larger selection than one? We keep a list of K elements we've chosen, and only if the next one meets the appropriately decreasing probability over time, do we add it to our collection, bumping an old value randomly:
def random_elements(seq, k):
"""Return `k` elements chosen randomly from `seq`."""
them = []
for n, elem in enumerate(seq):
if len(them) < k:
them.append(elem)
else:
if random.randint(0, n) < k:
them[random.randint(0, k-1)] = elem
return them
Now the Nth element has a k/N chance of being in the result, so we modify our selection criteria, and if it's chosen, we choose an old value to replace.
Sometimes our collection is not random access, so we have no choice but to traverse it completely in the worst case.
public static <T> List<T> randomSample3(List<T> items, int m){ ArrayList<T> res = new ArrayList<T>(m); int visited = 0; Iterator<T> it = items.iterator(); while (m > 0){ T item = it.next(); if (rnd.nextDouble() < ((double)m)/(items.size() - visited)){ res.add(item); m--; } visited++; } return res;}Stream of items
- public class LinkedListSampler {
- private static Random rand = new Random();
- public static <T> List<T> sample(
- LinkedList<T> list, int m) {
- ArrayList<T> samples = new ArrayList<T>(m);
- int k = 0;
- for (T element : list) {
- int pos = k++;
- if (pos < m) {
- samples.add(element);
- } else if ((pos = rand.nextInt(k)) < m) {
- samples.set(pos, element);
- }
- }
- return samples;
- }
- }
What happens if we don’t want the time complexity to be dependent on N, and the collection is read only?
In this case, assuming the collection is random access, we can use Floyd’s algorithm, which is both brilliant and easy to implement. It iterates with variable i through the last m indexes of the collection, and on each iteration adds a single item from the range 0..i, with a non-uniform distribution:
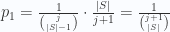
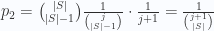
http://blog.codinghorror.com/shuffling/
Read full article from Fisher–Yates shuffle - Wikipedia, the free encyclopedia
In this case, assuming the collection is random access, we can use Floyd’s algorithm, which is both brilliant and easy to implement. It iterates with variable i through the last m indexes of the collection, and on each iteration adds a single item from the range 0..i, with a non-uniform distribution:
public static <T> Set<T> randomSample4(List<T> items, int m){ HashSet<T> res = new HashSet<T>(m); int n = items.size(); for(int i=n-m;i<n;i++){ int pos = rnd.nextInt(i+1); T item = items.get(pos); if (res.contains(item)) res.add(items.get(i)); else res.add(item); } return res;}
The time complexity is O(m) on the average, but we can bound the worst case time by O(m log(m)) if we use a balanced tree instead of a hash set.
The correctness follows by proving the following loop invariant: After completing an iteration with i=j, the set res contains a uniformly distributed random subset of size j-n+m+1 of the items in the range 0..j. We will prove this by induction on i. For the initial value of i (i=n-m), we simply choose a random position in the range 0..i, so it is also a random subset of size 1 of the same range. Now, let i=j (>n-m), and let S be any subset of size j-n+m+1 from the range 0..j. If items[j] is in S, then the previous iterations must have completed with res=S-{items[j]}, and then either position j or any previously selected position should be chosen. Using the induction assumption, we can compute the probability of obtaining S as follows:
The correctness follows by proving the following loop invariant: After completing an iteration with i=j, the set res contains a uniformly distributed random subset of size j-n+m+1 of the items in the range 0..j. We will prove this by induction on i. For the initial value of i (i=n-m), we simply choose a random position in the range 0..i, so it is also a random subset of size 1 of the same range. Now, let i=j (>n-m), and let S be any subset of size j-n+m+1 from the range 0..j. If items[j] is in S, then the previous iterations must have completed with res=S-{items[j]}, and then either position j or any previously selected position should be chosen. Using the induction assumption, we can compute the probability of obtaining S as follows:
If on the other hand items[j] is not in S, then we have many options of selecting |S|-1 items in the previous iterations, and then we should choose the remaining index:
In both cases we have a uniform probability for choosing |S| items from j+1 candidates, and that completes the proof.
Select a Random Node from a Singly Linked Listvoid printRandom(struct node *head){ // IF list is empty if (head == NULL) return; // Use a different seed value so that we don't get // same result each time we run this program srand(time(NULL)); // Initialize result as first node int result = head->key; // Iterate from the (k+1)th element to nth element struct node *current = head; int n; for (n=2; current!=NULL; n++) { // change result with probability 1/n if (rand() % n == 0) result = current->key; // Move to next node current = current->next; } printf("Randomly selected key is %d\n", result);}The standard way of implementing this algorithm is: associate each card with a random real number between 0.0 and 1.0. Sort the list based on its associated number. That's O(n log n) and has no bias.
As it turns out, the easiest way to implement a shuffle is by sorting. It's not exactly faster, as the typical sort is O(n log n) compared to the O(n) of the Knuth Fisher-Yates shuffle algorithm. We'll just sort by a random number-- in this case, a GUID.
var cards = Enumerable.Range(0, 51); var shuffledcards = cards.OrderBy(a => Guid.NewGuid());
JDK code:
public static void Collections.shuffle(List<?> list, Random rnd) {
int size = list.size();
if (size < SHUFFLE_THRESHOLD || list instanceof RandomAccess) {
for (int i=size; i>1; i--)
swap(list, i-1, rnd.nextInt(i));
} else {
Object arr[] = list.toArray();
// Shuffle array
for (int i=size; i>1; i--)
swap(arr, i-1, rnd.nextInt(i));
// Dump array back into list
// instead of using a raw type here, it's possible to capture
// the wildcard but it will require a call to a supplementary
// private method
ListIterator it = list.listIterator();
for (int i=0; i<arr.length; i++) {
it.next();
it.set(arr[i]);
}
}
}
http://bookshadow.com/weblog/2016/02/03/java-array-shuffle/Read full article from Fisher–Yates shuffle - Wikipedia, the free encyclopedia