LeetCode 889 - Construct Binary Tree from Preorder and Postorder Traversal

https://leetcode.com/articles/construct-binary-tree-from-preorder-and-postorder-/

Return any binary tree that matches the given preorder and postorder traversals.

Values in the traversals pre and post are distinct positive integers.

Example 1:

Input: pre = [1,2,4,5,3,6,7], post = [4,5,2,6,7,3,1]
Output: [1,2,3,4,5,6,7]

Note:

• 1 <= pre.length == post.length <= 30
• pre[] and post[] are both permutations of 1, 2, ..., pre.length.
• It is guaranteed an answer exists. If there exists multiple answers, you can return any of them

https://leetcode.com/problems/construct-binary-tree-from-preorder-and-postorder-traversal/discuss/161268/C%2B%2BJavaPython-One-Pass-Real-O(N)

I see a lot of solution saying O(N), but actually not.
If it takes already O(N) time to find left part and right right, it could not be O(N).
If it is recursive solution, it should use a hashmap to reduce complexity, otherwise in most cases it has at least average O(NlogN).

Here I share my iterative solution.
We will preorder generate TreeNodes, push them to stack and postorder pop them out.

1. Loop on pre array and construct node one by one.
2. stack save the current path of tree.
3. node = new TreeNode(pre[i]), if not left child, add node to the left. otherwise add it to the right.
4. If we meet a same value in the pre and post, it means we complete the construction for current subtree. We pop it from stack

Complexity:
O(N) Time O(N) Space

    public TreeNode constructFromPrePost(int[] pre, int[] post) {
        Deque<TreeNode> s = new ArrayDeque<>();
        s.offer(new TreeNode(pre[0]));
        for (int i = 1, j = 0; i < pre.length; ++i) {
            TreeNode node = new TreeNode(pre[i]);
            while (s.getLast().val == post[j]) {
                s.pollLast(); j++;
            }
            if (s.getLast().left == null) s.getLast().left = node;
            else s.getLast().right = node;
            s.offer(node);
        }
        return s.getFirst();
    }

Actually we don't need a deque, i find using a stack easier to understand:

 public TreeNode constructFromPrePost(int[] pre, int[] post) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode root = new TreeNode(pre[0]);
        stack.push(root);
        for (int i = 1, j = 0; i < pre.length; ++i) {
            TreeNode node = new TreeNode(pre[i]);
            while (stack.peek().val == post[j]) {
                stack.pop();
                j++;
            }
            if (stack.peek().left == null) {
                stack.peek().left = node;
            } else {
                stack.peek().right = node;
            }
            stack.push(node);
        }
        return root;
    }

X. Map to cache
https://leetcode.com/problems/construct-binary-tree-from-preorder-and-postorder-traversal/discuss/161286/C%2B%2B-O(N)-recursive-solution

For two subarrays pre[a,b] and post[c,d], if we want to reconstruct a tree from them, we know that pre[a]==post[d] is the root node.

[root][......left......][...right..]  ---pre
[......left......][...right..][root]  ---post

pre[a+1] is the root node of the left subtree.
Find the index of pre[a+1] in post, then we know the left subtree should be constructed from pre[a+1, a+idx-c+1] and post[c, idx].

https://leetcode.com/problems/construct-binary-tree-from-preorder-and-postorder-traversal/discuss/161281/Clean-Java-O(N)

Map<Integer, Integer> postMap = new HashMap<>();

public TreeNode constructFromPrePost(int[] pre, int[] post) {
    int length = pre.length;
    for(int i = 0; i < post.length; i++) {
        postMap.put(post[i], i);
    }
    
    return build(0, length - 1, 0, length - 1, pre, post);
}

private TreeNode build(int preLeft, int preRight, int postLeft, int postRight, int[] pre, int[] post) {
    if(preLeft > preRight || postLeft > postRight) {
        return null;
    }
    
    TreeNode root = new TreeNode(pre[preLeft]);
    
    if(preLeft + 1 <= preRight) {
        int index = postMap.get(pre[preLeft + 1]);
        int sum = index - postLeft;
        root.left = build(preLeft + 1, preLeft + sum + 1, postLeft, index, pre, post);
        root.right = build(preLeft + sum + 2, preRight, index + 1, postRight - 1, pre, post);
    }

    return root;
}

X. https://leetcode.com/problems/construct-binary-tree-from-preorder-and-postorder-traversal/discuss/161372/Logical-Thinking-with-Code-Beats-99.89

    int preStart;

    public TreeNode constructFromPrePost(int[] pre, int[] post) {

        // corner cases to add

        preStart = 0;
        int n = post.length;
        return constructFromPrePostFrom(pre, post, 0, n - 1);
    }

    private TreeNode constructFromPrePostFrom(int[] pre, int[] post, int postStart, int postEnd) {

        if (postStart > postEnd) {
            return null;
        }

        int rootVal = post[postEnd];
        TreeNode root = new TreeNode(rootVal);
        preStart++;
        
        if (preStart == pre.length || postStart == postEnd) {
            return root;
        }
        
        int leftVal = pre[preStart];
        int lri = postStart;
        for (; lri <= postEnd; lri++) {
            if (post[lri] == leftVal) {
                break;
            }
        }
        
        root.left = constructFromPrePostFrom(pre, post, postStart, lri);
        root.right = constructFromPrePostFrom(pre, post, lri + 1, postEnd - 1);

        return root;
    }

public TreeNode constructFromPrePost(int[] pre, int[] post) {
    return buildTree(pre, post, 0, post.length - 1, new int[]{0});
}

TreeNode buildTree(int[] pre, int[] post, int left, int right, int[] index) {
    if(left > right) return null;
        
    index[0]++;
    TreeNode root = new TreeNode(post[right]);
    if(left == right) return root;
    
    int i = left;
    while(i <= right && post[i] != pre[index[0]])
        i++;
    
    root.left = buildTree(pre, post, left, i, index);
    root.right = buildTree(pre, post, i + 1, right - 1, index);
    return root;
}

https://zxi.mytechroad.com/blog/tree/leetcode-889-construct-binary-tree-from-preorder-and-postorder-traversal/

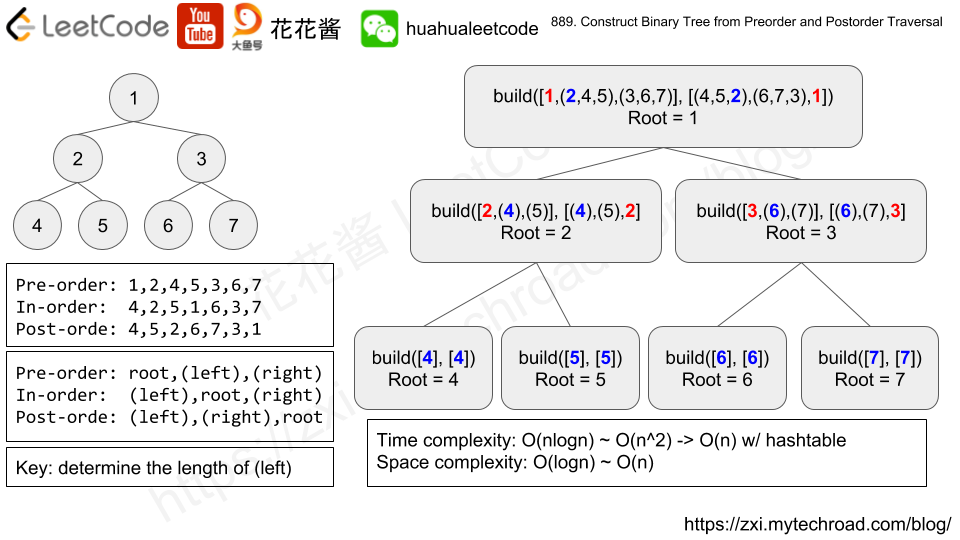
pre = [(root) (left-child) (right-child)]

post = [(left-child) (right-child) (root)]

We need to recursively find the first node in pre.left-child from post.left-child

e.g.

pre = [(1), (2,4,5), (3,6,7)]

post = [(4,5,2), (6,7,3), (1)]

First element of left-child is 2 and the length of it is 3.

root = new TreeNode(1)
root.left = build((2,4,5), (4,5,2))
root.right = build((3,6,7), (6,7,3))

Let's say the left branch has $L$ nodes. We know the head node of that left branch is pre[1], but it also occurs last in the postorder representation of the left branch. So pre[1] = post[L-1] (because of uniqueness of the node values.) Hence, L = post.indexOf(pre[1]) + 1.

Now in our recursion step, the left branch is represnted by pre[1 : L+1] and post[0 : L], while the right branch is represented by pre[L+1 : N] and post[L : N-1].

We present a variation of Approach 1 that uses indexes to refer to the subarrays of pre and post, instead of passing copies of those subarrays. Here, (i0, i1, N) refers to pre[i0:i0+N], post[i1:i1+N].

https://leetcode.com/problems/construct-binary-tree-from-preorder-and-postorder-traversal/discuss/161312/Simple-Java-using-Stack-with-explanation

1- We know that root always comes first in PreOrder but Last in Post Order. So, if we read PreOrder list from start, and check the position of the node in Post Order list, whatever nodes come before its index in PostOrder list is sub Node of this node (this node is the parent node for sure).
2- PreOrder always start from ROOT, then LEFT, and then RIGHT. So if the current node in PreOrder list has no left node, the next node in the list is its left node for sure (please refer to the NOTE), unless the next node index in PostOrder list is higher than the current node, since we know that in PostOrder we have LEFT,RIGHT, ROOT. So what ever node comes after the current node in our PreOrder list is a sub node of the current node as long as it's index is smaller than the current node index in our PostOrder list.
Note: We assume it is the left node, as it may have a right node which comes later. Since PreOrder is Root,Left,Right, and we start reading the list from 0 index, so we do not know whether the right node exists or not. What if it has a right node and we set the first sub node as its right node.

 public TreeNode constructFromPrePost(int[] pre, int[] post) {
     if(post==null || post.length==0 || pre==null || pre.length==0) return null;
     int len = post.length; 
     HashMap<Integer,Integer> index = new HashMap<>();
     for(int i=0; i<len; i++) index.put(post[i], i); //record the indexs
     Stack<TreeNode> stack = new Stack<>();
     int i=0;
     TreeNode root = new TreeNode(pre[i++]); //the first node in our PreOrder list is always the ROOT Node
     stack.push(root);
     while(i<len){  //start reading the PreOrder list and check the indexs with PostOrder list
      TreeNode next = new TreeNode(pre[i]);      
      while(index.get(stack.peek().val)<index.get(next.val)) stack.pop(); //we remove nodes with smaller index from stack as they cannot be the next nodes' parent
      TreeNode existing = stack.pop();       
      if(existing.left==null) { //left always come first
       existing.left=next;
       stack.push(existing); stack.push(next); // we push the existing node again into the stack as it may have a right node
      }
      else {
       existing.right=next;
       stack.push(next); // we do not push the existing node anymore, as it's left and right nodes already found
      }            
      i++;
     }
     return root;
    }

When we traverse the post and visit post[i], it means all child nodes in the tree of post[i] is visited already.
Thus, we can use pre to construct the tree while use post to figure out whether the node we visit still has unvisited children.

X.
https://leetcode.com/problems/construct-binary-tree-from-preorder-and-postorder-traversal/discuss/161281/Clean-Java-O(N)

The key point is 1: preprocessing. 2: Find the correct index

Map<Integer, Integer> postMap = new HashMap<>();

public TreeNode constructFromPrePost(int[] pre, int[] post) {
    int length = pre.length;
    for(int i = 0; i < post.length; i++) {
        postMap.put(post[i], i);
    }
    
    return build(0, length - 1, 0, length - 1, pre, post);
}

private TreeNode build(int preLeft, int preRight, int postLeft, int postRight, int[] pre, int[] post) {
    if(preLeft > preRight || postLeft > postRight) {
        return null;
    }
    
    TreeNode root = new TreeNode(pre[preLeft]);
    
    if(preLeft + 1 <= preRight) {
        int index = postMap.get(pre[preLeft + 1]);
        int sum = index - postLeft;
        root.left = build(preLeft + 1, preLeft + sum + 1, postLeft, postLeft + sum, pre, post);
        root.right = build(preLeft + sum + 2, preRight, postLeft + sum + 1, postRight - 1, pre, post);
    }

    return root;
}

    public TreeNode constructFromPrePost(int[] pre, int[] post) {
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < post.length; i++){
            map.put(post[i], i);
        }
        return dfs(pre, 0, pre.length - 1, post, 0, post.length - 1, map);
    }
    private TreeNode dfs(int[] pre, int preStart, int preEnd, int[] post, int postStart, int postEnd, Map<Integer, Integer> map){
        if (preStart > preEnd || postStart > postEnd){
            return null;
        }
        TreeNode root = new TreeNode(pre[preStart]);
        if (preStart + 1 <= preEnd){
            int deltaIndex = map.get(pre[preStart+1]) - postStart;
            root.left = dfs(pre, preStart + 1, preStart + 1 + deltaIndex, post, postStart, postStart + deltaIndex, map);
            root.right = dfs(pre,  preStart + 1 + deltaIndex + 1, preEnd, post, postStart + deltaIndex + 1, postEnd - 1, map);
        }
        return root;
    }

X. https://leetcode.com/articles/construct-binary-tree-from-preorder-and-postorder-/

A preorder traversal is:

• (root node) (preorder of left branch) (preorder of right branch)

While a postorder traversal is:

• (postorder of left branch) (postorder of right branch) (root node)

For example, if the final binary tree is [1, 2, 3, 4, 5, 6, 7] (serialized), then the preorder traversal is [1] + [2, 4, 5] + [3, 6, 7], while the postorder traversal is [4, 5, 2] + [6, 7, 3] + [1].

If we knew how many nodes the left branch had, we could partition these arrays as such, and use recursion to generate each branch of the tree.

Algorithm

Let's say the left branch has $L$ nodes. We know the head node of that left branch is pre[1], but it also occurs last in the postorder representation of the left branch. So pre[1] = post[L-1] (because of uniqueness of the node values.) Hence, L = post.indexOf(pre[1]) + 1.

Now in our recursion step, the left branch is represnted by pre[1 : L+1] and post[0 : L], while the right branch is represented by pre[L+1 : N] and post[L : N-1].

• Time Complexity: $O(N^2)$, where $N$ is the number of nodes.
• Space Complexity: $O(N^2)$. 

  public TreeNode constructFromPrePost(int[] pre, int[] post) {

    int N = pre.length;

    if (N == 0)

      return null;

    TreeNode root = new TreeNode(pre[0]);

    if (N == 1)

      return root;

    int L = 0;

    for (int i = 0; i < N; ++i)

      if (post[i] == pre[1])

        L = i + 1;

    root.left = constructFromPrePost(Arrays.copyOfRange(pre, 1, L + 1), Arrays.copyOfRange(post, 0, L));

    root.right = constructFromPrePost(Arrays.copyOfRange(pre, L + 1, N), Arrays.copyOfRange(post, L, N - 1));

    return root;

  }

We present a variation of Approach 1 that uses indexes to refer to the subarrays of pre and post, instead of passing copies of those subarrays. Here, (i0, i1, N) refers to pre[i0:i0+N], post[i1:i1+N].

  int[] pre, post;

  public TreeNode constructFromPrePost(int[] pre, int[] post) {

    this.pre = pre;

    this.post = post;

    return make(0, 0, pre.length);

  }

  public TreeNode make(int i0, int i1, int N) {

    if (N == 0)

      return null;

    TreeNode root = new TreeNode(pre[i0]);

    if (N == 1)

      return root;

    int L = 1;

    for (; L < N; ++L)

      if (post[i1 + L - 1] == pre[i0 + 1])

        break;

    root.left = make(i0 + 1, i1, L);

    root.right = make(i0 + L + 1, i1 + L, N - 1 - L);

    return root;

  }